15.3. Характеристики точности ар алгоритма.
Характеристики точности (ХТ) измерения частоты для несмещенных оценок обычно представляются в виде зависимости дисперсии ошибки измерения частоты гармонического сигнала σ2 от отношения сигнал/шумq. В качестве базы для сравнения принято использовать асимптотический предел Крамера-Рао, который при воздействии аддитивного нормального белого (дельта-коррелированного) шума имеет вид:
.
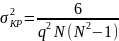(15.8)
Для АР алгоритма ПОЛП также теоретически получены асимптотические пределы, которые, кроме ОСШq и размером выборки N, определяются порядком моделиК:
.
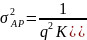(15.9)
Асимптотический предел АР алгоритма минимален при К=N/3 и превышает теоретический предел точности Крамера-Рао всего на 0,5 дБ.
Как известно, асимптотически оптимальной оценкой частоты одиночного гармонического сигнала является оценка максимального правдоподобия (МП), которая реализуется путем вычисления абсолютного максимума зависимости отношения правдоподобия от оцениваемого параметра, в данном случае частоты сигнала. При воздействии нормального белого шума и равномерно распределенных на интервалах оценивания неизвестной частоты и фазы эта процедура эквивалентна и может быть сведена к вычислению абсолютного максимума модуля корреляционного интеграла.
На рисунке 15.5 приведены характеристики точности измерения частоты гармонического сигнала для АР методаПОЛП (сплошные линии) и метода МП (пунктирная линия).
Дисперсии ошибки измерения частоты метода МП асимптотически стремиться к пределу КР (нижняя штрих-пунктирная прямая). Дисперсии ошибки измерения частоты АР метода при длине выборки N=5 и порядках АР модели К=1 и К=2≈N/3 асимптотически стремятся к своим пределам, полученным в соответствии с формулой (15.9) (верхние штрих-пунктирные прямые).
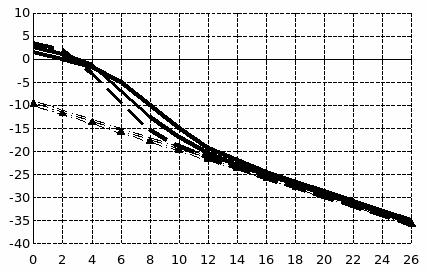
Рис.15.5.
Как видно из графиков, у ХТ обеих оценок можно выделить три области. При больших отношениях сигнал/шум имеет место область асимптотического приближения к потенциально достижимым границам. При средних значениях сигнал/шум имеет место переходная область или область отсечки. И, наконец, при малых значениях сигнал/шум наблюдается область аномальных оценок, когда влияние аддитивного шума затрудняет определение абсолютного максимума. Рабочей зоной обычно считается область асимптотического приближения. Приведенный пример показывает, что АР оценки частоты по методу ПОЛП являются асимптотически оптимальными и проигрывают оптимальным оценкам МП не более 1 дБ в переходной и асимптотической областях.
Если процедуру оценивания совместить с процедурой обнаружения таким образом, чтобы действительными оценками частоты считались оценки только обнаруженных сигналов, что обычно реализуется на практике, то ХТ могут быть существенно улучшены, особенно в переходной и аномальной областях. Как следует из рис. 15.6 (обозначения идентичны принятым на рис. 15.5), это формально приводит к превышению потенциального предела КР, что объясняется тем, что за счет процедуры обнаружения из рассмотрения удалены все оценки с «неудачным» отношением сигнал/шум, имеющим «плохую» точность. Приведенный пример показывает, что АР обработка сигналов может рассматриваться как совместный алгоритм обнаружения и оценивания.
При оценивании частоты гармонического сигнала с неизвестной амплитудой, распределенной по рэлеевскому закону, характер зависимостей оценок МП и АР оценок изменяется: существенно увеличивается переходная область или область отсечки. Это объясняется тем, что при фиксированном среднем отношении сигнал/шум отдельные измерения за счет флуктуаций амплитуды могут происходить как при улучшенном отношении сигнал/шум, так и при ухудшенном. При этом процедура отсечки «неудачных» реализаций сигнала в обнаружителе приводит к улучшению ХТ, аналогичному приведенному на рис. 15.6.
Рис.15.6.