
- •Министерство образования и науки Российской Федерации
- •Конспект лекций по курсу «морская радиолокация»
- •Введение в морскую радиолокацию
- •Историческая справка
- •Основные термины и определения
- •Классификация морских рлс
- •Основные задачи радиолокации
- •2. Влияние морских условий на работу радиолокатора
- •2.1.Основное уравнение радиолокации для морских условий
- •2.2. Зона видимости рлс над морской поверхностью
- •2.3. Приповерхностный волновод
- •3. Описание морской поверхности
- •3.1. Характеристики морского волнения
- •3.2.Двумерный спектр морского волнения
- •3.3.Факторизация двумерного спектра морского волнения в виде произведения одномерных спектров
- •4. Отражения от морской поверхности
- •4.1.Удельная эпр морской поверхности
- •4.2.Описание отраженного морем сигнала на основе функции рассеяния.
- •5. Зондирующие сигналы морских рлс
- •5.1. Требования к зондирующим сигналам морских рлс и их классификация
- •Основные тенденции развития зондирующих сигналов
- •6.Избранные вопросы теории обнаружения и оценивания параметров сигналов
- •6.1. Постановка классической задачи обнаружения сигнала
- •7. Реализация корреляционного (согласованного) приема
- •7.1. Корреляционный приемник (коррелятор)
- •7.2. Согласованная фильтрация
- •8. Функция неопределенности и ее связь с выходом коррелятора и согласованного фильтра
- •8.1. Функция неопределенности
- •8.2.Связь фн с выходом согласованного фильтра и коррелятора.
- •8.3. Свойства фн
- •8.4. Взаимная фн (вфн).
- •11. Основные определения и модели пространственно-временных сигналов
- •12. Спектральнаятрактовказадачиоптимальнойобработкисигналов
- •13. Обзор параметрических методов обработки сигналов
- •14. Авторегрессионная обработка сигналов
- •15. Показатели качества параметрических методов обработки сигналов.
- •15.1. Рабочие статистики обнаружения и оценивания (на примере ар методов)
- •15.2. Характеристики обнаружения ар алгоритма.
- •15.3. Характеристики точности ар алгоритма.
- •16.Основы траекторной обработки радиолокационной информации
- •17. Расчет зоны видимости рлс в свободном пространстве
- •17.1. Расчет зоны видимости рлс в свободном пространстве.
- •17.2.Расчет зоны видимости рлс с учетом подстилающей поверхности
- •18. Совместная обработка радиолокационной информации
14. Авторегрессионная обработка сигналов
Спектральный анализ на основе АР моделей возник как эмпирический метод и получил теоретическое обоснование в рамках критерия максимальной энтропии (МЭ), введенного Дж. Бэргом, и теории линейного предсказания (ЛП), разработанной Н.Винером и А.Н.Колмогоровым и развитой Н. Левинсоном. Критерий максимальной энтропии предполагает при предсказании данных за пределами анализируемой выборки не увеличивать количества информации, содержащейся в исходных (измеренных) данных, путем фиксации удельной энтропии на максимальном для данной выборки уровне. Поскольку критерий МЭ не учитывает в явном виде наличие шума, обычно сопутствующего измерениям, предполагается, что данные известны точно, или, что эквивалентно, известна автокорреляционная последовательность вида:
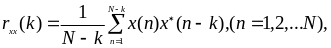 (14.1)
(14.1)
поэтому критерий МЭ приводит к использованию АР-моделей максимальной длины К=N-1. При отсутствии шума это не вызывает нежелательных эффектов типа появления “лишних” максимумов в оценке СПМ, поскольку происходит естественное согласование порядка АР-модели с порядком анализируемого процесса за счет обнуления излишних АР-параметров аk. Присутствие шума или незначительные отклонения процесса от чисто авторегрессионного приводят к появлению ложных максимумов и другим искажениям оценки СПМ по методу МЭ. Это происходит из-за плохой статистической обусловленности значений автокорреляционной последовательности с максимальными сдвигами, оцениваемыми по измеренной выборке (один член в сумме при k=N-1).
В методах линейного предсказания уравнения, на основе которых осуществляется предсказание, идентичны АР-уравнениям вида (13.8) и (13.9) с той лишь разницей, что в уравнениях ЛП учитывается присутствие шума:
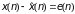 (14.2)
(14.2)
где предсказанное
значение
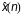 можно определить в прямом и обратном
направлениях следующими выражениями:
можно определить в прямом и обратном
направлениях следующими выражениями:
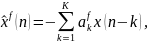 (14.3)
(14.3)
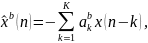 (14.4)
(14.4)
а параметры
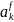 и
и
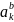 имеют смысл АР-параметров. Можно показать,
что для стационарных процессов параметры
и
связаны как комплексно-сопряженные
величины, поэтому верхний индекс может
быть в дальнейшем опущен, так как
=ak
и
=
имеют смысл АР-параметров. Можно показать,
что для стационарных процессов параметры
и
связаны как комплексно-сопряженные
величины, поэтому верхний индекс может
быть в дальнейшем опущен, так как
=ak
и
=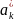 .
Критерием предсказания является
минимизация суммарной мощности ошибок
предсказания PK
.
Критерием предсказания является
минимизация суммарной мощности ошибок
предсказания PK ,
состоящей из элементарных ошибок вида
(14.2), вычисленных в пределах выборки
длинной N
отсчетов в прямом и обратном направлениях:
,
состоящей из элементарных ошибок вида
(14.2), вычисленных в пределах выборки
длинной N
отсчетов в прямом и обратном направлениях:
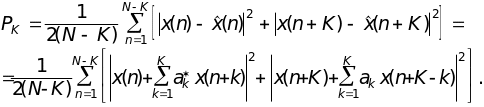 (14.5)
(14.5)
Отыскание АР-параметров ak возможно путем решения системы линейных уравнений, получаемых приравниванием нулю частных производных суммарной мощности ошибок предсказания РК по всем ak, которая является вогнутой функцией этих параметров при анализе эквидистантных выборок и поэтому имеет единственный минимум:
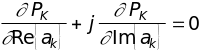 ,
(k=1,2,...,K).
(14.6)
,
(k=1,2,...,K).
(14.6)
В матричной форме полученная система уравнений может быть записана в виде:
RKaK=2
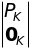 ,
(14.7)
,
(14.7)
где: RK-теплицева матрица с элементами
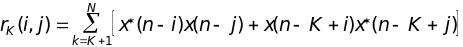 ,
(14.8)
,
(14.8)
aK-вектор
параметров, имеющий вид
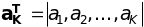 ,
0K-нуль-вектор
(вектор с нулевыми элементами) размером
К.
,
0K-нуль-вектор
(вектор с нулевыми элементами) размером
К.
Алгоритм, основанный на решении уравнения (14.7), известен в литературе как ковариационный. Среди многообразия других АР-алгоритмов он отличается наивысшими характеристиками точности и рэлеевского разрешения, однако при этом не гарантируется получения устойчивого решения с полюсами внутри единичной окружности. Это может приводить к аномальным оценкам СПМ, в которых будут пропущены гармонические или узкополосные компоненты. Для радиолокационного обнаружения это эквивалентно пропуску целей.
От этого недостатка свободен алгоритм гармонического среднего или алгоритм Бэрга, называемый в некоторых источниках методом прямого и обратного линейного предсказания (ПОЛП). В алгоритме используется рекуррентный метод решения систем линейных уравнений Левинсона-Дурбина, который предполагает получение решения aK на последующем шаге рекурсии при порядке АР-модели К на основе решения aK-1, полученного на предыдущем шаге при порядке модели К-1. Это эквивалентно последовательной минимизации суммарной ошибки предсказанияРК только по последнему параметру аК. Алгоритм допускает интерпретацию в виде решетчатого фильтра предсказания ошибки (рис. 14.1), коэффициенты отражения которого k имеют смысл частных коэффициентов корреляции ошибок предсказания в прямом и обратном направлениях:
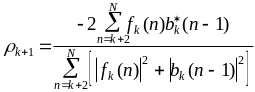 ,
(14.9)
,
(14.9)
где ошибки прямого
и обратного предсказания на выходе К-ой
ступени решетчатого фильтра обозначены
соответственно как
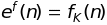 и
и
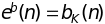 ,
а z-1
означает задержку на один такт (отсчет).
,
а z-1
означает задержку на один такт (отсчет).
f







Z-1
Z-1
 0(n)
f1(n)
f2(n)
fk(n)
fK(n)
0(n)
f1(n)
f2(n)
fk(n)
fK(n)
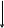
1* 2*k*K*
x (n)
(n)
Z-1
 12kK
12kK
Z-1
b0(n) b1(n) b2(n) bk(n) bK(n)
Ступень 1 Ступень 2 Ступень k Ступень К
Рис. 14.1. Решетчатый фильтр предсказания ошибки в прямом и обратном направлениях.
Коэффициенты отражения решетчатого фильтра предсказания k однозначно связаны с АР-параметрами ak, что позволяет производить минимизацию суммарной мощности ошибки предсказания на основе уравнений вида:
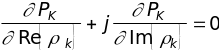 , (k=1,2,...,K).
(14.10)
, (k=1,2,...,K).
(14.10)
При этом АР-параметры для последующей ступени решетчатого фильтра определяются по рекуррентному соотношению Левинсона:
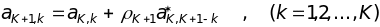 .
(14.11)
.
(14.11)
Заметим, что всегда аK,K=K и аK,0=1. Мощность ошибки прямого и обратного предсказания РК можно вычислить также по рекуррентной формуле через коэффициенты отражения решетчатого фильтра:
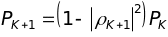 ,
(14.12)
,
(14.12)
откуда очевидна ее монотонно спадающая зависимость от порядка АР-модели. Для ошибок прямого и обратного предсказания справедливы соотношения:
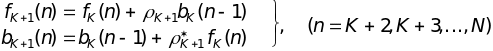 .
(14.13)
.
(14.13)
Подставляя (14.13) в (14.10) и решая уравнение относительно k+1, приходим к выражению (14.9). Математические основы рекурсивного решения систем нормальных линейных уравнений Юла-Уоккера с теплицевой структурой корреляционной матрицы можно найти в работе Блейхута, а подробный вывод алгоритма ПОЛП изложен в работе Марпла.
C учетом приведенных формул (14.9), (14.11), (14.12) и (14.13) рекуррентный алгоритм ПОЛП принимает вид:
1) Определяются исходные условия как:
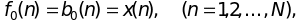 (14.14)
(14.14)
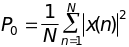 .
(14.15)
.
(14.15)
2)Вычисляются коэффициент отражения первой ступени решетчатого фильтра:
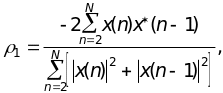 (14.16)
(14.16)
и средняя мощность ошибки предсказания на выходе первой ступени фильтра:
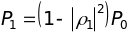 .
(14.17)
.
(14.17)
Из формулы Левинсона (14.11) определяется АР-параметр для первого порядка модели:
а1,1=1. (14.18)
3) Вычисляются ошибки прямого f1(n) и обратного b1(n) предсказания на выходе первой ступени фильтра:
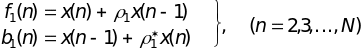 .
(14.19)
.
(14.19)
на основании которых определяется следующий коэффициент отражения:
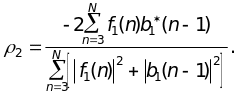 (14.20)
(14.20)
Параметры АР-модели второго порядка находятся как:
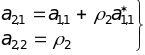 .
(14.21)
.
(14.21)
Завершается расчет для второй ступени фильтра вычислением суммарной мощности ошибки:
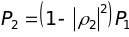 .
(14.22)
.
(14.22)
Рекурсии для последующих порядков фильтров очевидны и не представляют труда при реализации.
После того, как найден вектор АР- параметров aK для требуемого порядка модели, оценка СПМ может быть вычислена по формуле (13.13) или представлена через полюса:
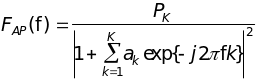 =
=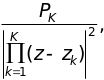 (14.23)
(14.23)
где zk - комплексные полюса, являющиеся решением характеристического уравнения A(z)=0, образованного приравниванием нулю полинома-знаменателя оценки СПМ (13.13) после выполнения z-преобразования вида z=exp{j2f}:
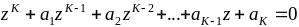 .
(14.24)
.
(14.24)
Полюса могут быть представлены через свои модули и аргументы:
zk=zkexp{jarg(zk)} (14.25)
К достоинствам рекуррентного алгоритма ПОЛП относятся несомненная простота реализации и возможность получения АР-параметров для всех порядков модели, начиная с первого и до максимального значения. Кроме того, в алгоритме ПОЛП имеется возможность оценивания порядка анализируемого процесса на основе сопоставления значений мощностей ошибки предсказания, полученных при различных порядках АР-модели. Получение устойчивых решений системы линейных уравнений, т.е. решений, при которых все полюса гарантированно попадают в единичную окружность на комплексной плоскости, делают алгоритм ПОЛП предпочтительным в классе АР алгоритмов при решении задач статистического разрешения-обнаружения, поскольку в этом случае обеспечивается более адекватная передача амплитудных соотношений в оценке СПМ. Заметим, что факторизация знаменателя передаточной функции АР-оценки СПМ (13.10) в виде произведения двух комплексно-сопряженных полиномов A(z)A*(1/z*) позволяет найти устойчивое решение для любого АР-алгоритма, однако для этого требуется дополнительный анализ модулей комплексных корней характеристических полиномов A(z). Свойства этих корней позволяют заключить, что устойчивость решения АР-уравнений не влияет на точность оценивания частоты гармонических компонент в АР-оценках СПМ.
Одно из важных свойств алгоритма ПОЛП, вытекающее из его интерпретации в виде решетчатого фильтра предсказания ошибки, заключается в возможности его использования для выбеливания окрашенных шумов и узкополосных помех, если они адекватно представимы процессами авторегресси. Это свойство используется в системах ПВО с адаптивным формированием пространственных и частотных характеристик. Из этого же свойства вытекает возможность оценки мощности входного шума, которая может использоваться как для компенсации его влияния на алгоритмы обработки с целью улучшения их показателей качества, так и для придания процедуре обнаружения свойств стабилизации вероятности ложных тревог.
