13. Обзор параметрических методов обработки сигналов

Параметрические методы обработки сигналов возникли и развиваются как методы спектрального оценивания. В отличие от методов спектрального анализа, когда в результате некоторого спектрального преобразования исходной непрерывной s(t) или дискретной s(n) функции оцениваются амплитудные A(f) и фазовые (f) зависимости (спектры) в базисе выбранных ортогональных или квазиортоганальных функций, спектральное оценивание решает более узкую задачу оценки спектральной плотности мощности (СПМ) F(f)=A(f)², хотя параметрические методы также допускают понятие оценки фазового спектра, несущего определенную информационную нагрузку. В литературе принято параметрические методы считать альтернативными по отношению к методам, основанным на ортогональном спектральном разложении, однако все параметрические методы предполагают представление оценок СПМ в базисе общепринятых (чаще всего гармонических) ортогональных функций.

В основе большинства параметрических методов лежит идея аппроксимации анализируемого сигнала с помощью некоторой модели, представляющей собой, как правило, алгебраическое, тригонометрическое, экспоненциальное, дифференциальное или разностное уравнение, параметры которых подгоняются к конкретной реализации анализируемого сигнала на основе того или иного критерия. После того, как найдены параметры модели и анализируемая реализация сигнала (рис. 13.1, сплошная кривая) на интервале наблюдения может быть аппроксимирована с удовлетворительной точностью (пунктирная кривая на рис. 13.1), оценку СПМ можно вычислять не по ограниченной выборке реального сигнала (ограничена двумя пунктирными вертикальными прямыми), а на основе генерируемого моделью “синтетического” сигнала, пределы существования которого неограниченны (штрихпунктирная кривая на рис 13.1).

Рис. 13.1.

Для точной аппроксимации анализируемого сигнала необходимо выполнение двух условий:

(a) - модель должна обеспечивать возможность адекватного отображения сигнала во всем многообразии возможных сочетаний его параметров;

(b) - сопутствующие измерениям шумы должны отсутствовать.

Условие (а) можно трактовать как возможность порождения моделью анализируемого сигнала. При выполнении этих условий спектральное оценивание эквивалентно анализу полезного сигнала бесконечной длительности. Очевидно, что применение такого алгоритма обработки как ПФ обеспечит в этом случае идеальную точность и бесконечно малую разрешающую способность по всем оцениваемым параметрам, как и должно быть в соответствии с постулатами теории статистического разрешения. В присутствии шумов измерений и при отклонении моделируемого “синтетического” сигнала от анализируемого его подгонка к реальной выборке будет приближенной, что приводит к ухудшению точностных и других статистических характеристик параметрических методов, тем больших, чем выше уровень шума и больше нарушения адекватности. Здесь уместно акцентировать внимание на отличии постановки задачи спектрального оценивания как задачи нахождения некоторой функции частоты от задачи оценивания параметров отдельных составляющих спектральной оценки, например, частоты и/или амплитуды синусоиды в шуме. В более тонкой трактовке задача может формулироваться как задача оценивания СПМ полезного сигнала, т.е. нахождения некоторой функции частоты, соответствующей полезной компоненте анализируемого сигнала. Различие подходов можно проиллюстрировать на примере РЛС обзора морской поверхности (рис.13.2). В случае обнаружения сигнала от движущегося судна на фоне помех от морской поверхности и собственных шумов приемника (сплошная кривая на рисунке 13.2, а) задача первичной обработки сводится к получению оценок амплитуды и частоты полезного гармонического сигнала (пунктирная криваяна рисунке 13.2, а), получение оценки СПМ анализируемого сигнала (штрихпунктирная кривая на рисунке 13.2, а) не представляет интереса. В случае измерения гидрофизических параметров морского волнения задача сводится к получению оценки СПМ полезного сигнала, представляющей собой оценку спектра отраженного морем сигнала (сплошная кривая на рисунке 13.2, б). Адекватное отображение белого шума и других мешающих компонент в данной постановке не является обязательным (штрихпунктирная кривая на рисунке 13.2, б). Однако оценка СПМ, полученная с помощью неадекватной моделиприводит к неудовлетворительному результату (пунктирная кривая на рисунке 13.2, б).

а) б)

Рис. 13.2.

Методологическое значение этих различий заключается в выборе базовых характеристик, показателей качества и критериев для сравнения методов обработки сигналов, а также синтезе алгоритмов обработки и рабочих статистик.

Обзор основных типов моделей, нашедших широкое практическое применение, начнем с моделей, имеющих рациональную передаточную (системную) функцию:

Н(z)=B(z)/A(z), (13.1)

где A(z) и B(z) - полиномы переменной z=exp{j2f}. В общем случае эти модели относятся к моделям авторегрессии - скользящего среднего (АРСС) и при дискретном представлении входного x(n) и выходного y(n) сигналов описываются разностным уравнением вида:

x(n)=-a₁x(n-1)-a₂x(n-2)-...-a_Kx(n-K)+b₀y(n)+b₁y(n-1)+...+b_Ly(n-L). (13.2)

Коэффициенты a_k и b_l являются параметрами АРСС модели и однозначно определяют передаточную функцию H(z). Обычно полагают а₀=1, что достигается простой нормировкой уравнения (13.2), поэтому H(z) имеет вид:

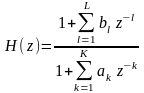. (13.3)

Для сигналов с непрерывным временем (или иным параметром, относительно которого используется модель) разностное уравнение (13.2) заменяется дифференциальным уравнениям вида:

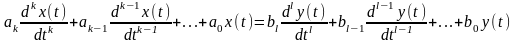,(13.4)

где x(t)и y(t) - входной и выходной сигнал алгоритма обработки. Приравнивая a_k=0 при k1 и полагая по-прежнему а₀=1, приходим к модели скользящего среднего (СС), которая описывается уравнением вида:

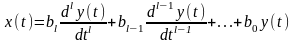, (13.5)

при непрерывных сигналах и вида:

x(n)=b₀y(n)+b₁y(n-1)+...+b_Ly(n-L), (13.6)

при дискретных. Передаточная функция, соответствующая СС модели, имеет вид полинома- числителя (13.3):

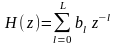. (13.7)

В случае, когда в уравнениях (13.2) и (13.4) все коэффициенты b_l=0, получаем модель авторегрессии (АР), которой соответствуют уравнения в дифференциальном виде:

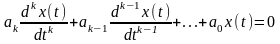, (13.8)

и разностном виде:

x(n)=-a₁x(n-1)-a₂x(n-2)-...-a_Kx(n-K).(13.9)

Передаточная функция, соответствующая АР модели, имеет вид полинома - знаменателя (13.3):

. (13.10)

Оценка спектральной плотности мощности при использовании АРСС модели определяется передаточной функцией (13.3) и для дискретного представления сигнала с нормированным шагом дискретизации t=1 имеет вид:

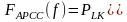, (13.11)

где P_LK - мощность порождающего белого шума, при пропускании которого через фильтр с передаточной характеристикой вида (13.3) генерируется данный АРСС процесс, описываемый уравнением вида (13.4). Здесь и далее под частотой f будем понимать нормированную к шагу дискретизации безразмерную частоту, такую что f[-0,5;+0,5].

Для СС модели оценка СПМ в соответствии с (13.7) примет вид:

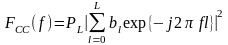, (13.12)

где P_Lтакже имеет смысл мощности порождающего белого шума. Наконец, АР модели соответствует оценка СПМ вида:

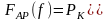. (13.13)

В соответствии с основной теоремой алгебры полиномы А(z)и В(z)могут быть разложены на простые сомножители. Для этого необходимо найти корни уравнений А(z)=0 и В(z)=0, которые называют в первом случае полюсами для полинома - знаменателя и нулями во втором для полинома - числителя. Соответственно через нули и полюса могут быть выражены и оценки СПМ (13.11) - (13.13).

АРСС модели обладают более широкими возможностями адекватного отображения спектров сигналов, нежели АР или СС модели, являющиеся частными случаями первых, однако нахождение параметров модели а_k и b_l сопряжено с рядом вычислительных трудностей. В силу нелинейного характера уравнения для нахождения параметров решение обычно ищут с помощью приближенных итеративных методов, но эти методы требуют больших вычислительных затрат, не всегда гарантируют сходимости и нахождение истинного решения, поэтому не могут быть рекомендованы для обработки сигналов в реальном времени. В настоящее время разработаны субоптимальные алгоритмы раздельного (поочередного) нахождения АР и СС параметров, однако их показатели качества недостаточно изучены и зависят от характера анализируемого процесса.

С использованием АР моделей тесно связан метод минимума дисперсии (иногда необоснованно именуемый в литературе методом максимального правдоподобия), который в равной степени может быть отнесен к адаптивным методам. Суть метода заключается в минимизации дисперсии на выходе трансверсального фильтра с К+1 коэффициентами с₀, с₁,...,с_К, выходной сигнал которого y(n) связан с входным сигналом х(n) сверткой вида:

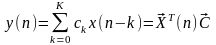, (13.14)

где: 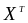(n)={x(n),x(n-1),...,x(n-K)}; 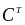={c₀ ,c₁,...,c_K}. Накладывая ограничения на передачу без искажений и потерь компоненты сигнала с частотой f₀ вида:

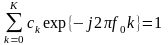, (13.15)

можно показать, что оценка СПМ по методу минимума дисперсии (МД) К-го порядка эквивалентна выражению:

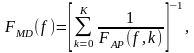(13.16)

где F_AP(f,k)– АРоценка СПМ, соответствующая k-му порядку АР модели вида (13.13). Таким образом, МД оценка СПМ может быть найдена на основе усреднения АРоценок СПМ для порядков k=0,1,...K. Хотя МДоценка обладает худшим разрешением по частотному параметру, чем АРоценка того же порядка, их применение бывает оправдано в тех случаях, когда необходимо более точное измерение амплитудных соотношений в оцениваемом спектре.

Следующую группу составляют тригонометрические (для действительных данных) или экспоненциальные (для комплексных данных) модели. В общем виде такая модель состоит из конечного числа комплексных гармоник:

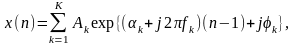(n=1,2,...,N), (13.17)

где: А_k- амплитуда, _k - коэффициент затухания, f_k - частота и _k - начальная фаза k-ой экспоненты. При_k=0 для всех k=1,2,...,K имеем модель из незатухающих экспонент. Заметим, что ПФ удовлетворяет незатухающей экспоненциальной модели при фиксированном эквидистантном наборе f_k.

Одним из наиболее известных методов, основанных на экспоненциальных или тригонометрических моделях вида (13.17), является метод Прони. В общем случае при подгонке модели к имеющимся данным варьируются все параметры: А_k,_k, f_k,_k, включая К. Однако даже при фиксированных порядках модели К2 задача нахождения параметров модели принципиально нелинейна и не имеет строгого аналитического решения. Приближенные итеративные методы, такие как процедура наискорейшего градиентного спуска, требуют больших вычислительных затрат и не всегда сходятся к правильному решению. Метод Прони, являясь субоптимальным, позволяет разделить процедуру нахождения параметровА_k,_k и _k, f_k при заданном К, сведя ее к решению линейных уравнений при условии N2K. Сам метод Прони не обеспечивает получения оценки СПМ, а дает лишь оценки параметров комплексных гармоник. Тем не менее, на его основе можно получить и оценку СПМ, применив к полученным данным какую-либо процедуру спектрального оценивания, например, ПФ.

К достоинствам экспоненциальных моделей относится высокая точность измерения параметров гармонических компонент. В тоже время эти модели работают неудовлетворительно, если в анализируемом сигнале присутствуют гладко окрашенные по спектру составляющие. Они также теряют работоспособность и при невысоких ОСШ. Это связано с тем, что в методе Прони не учитывается наличие белого или окрашенного шума в анализируемых данных, он не допускает интерпретации шума как порождающего шумового процесса, как это имело место в АРСС-моделях. Все это обуславливает ограниченное применение в радиолокационной практике экспоненциальных и тригонометрических моделей и метода Прони.

Помимо тригонометрических и экспоненциальных функций в методе Прони могут использоваться другие аналитические функции. В общем виде модель можно записать как:

(13.18)

где 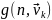- однозначная непрерывная функция, вектор параметров которой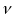 имеет значение 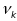. В частности, функция может иметь вид закона модуляции амплитуды, частоты или фазы излучаемого сигнала и отличаться значением таких параметров, как задержка или доплеровский сдвиг частоты. Однако при любых метод характеризуется пониженной устойчивостью к воздействию аддитивных шумов, что проявляется в ухудшении его обнаруженческих способностей.

К параметрическим методам спектрального оценивания относят большую группу методов, основанных на анализе собственных значений автокорреляционной матрицы или ее оценки. Принципиальным отличием этих методов является разделение информации, содержащейся в автокорреляционной матрице, на два ортогональных векторных подпространства - подпространство сигналов и подпространство шума. Данная группа методов имеет значение и может применяться как в качестве самостоятельных методов спектрального оценивания, так и в качестве дополнительной процедуры, предваряющей обработку исходных данных и улучшающей показатели качества других параметрических методов, если анализируемые данные состоят из аддитивной смеси комплексных гармоник и белого шума. Рассмотрим экспоненциальную модель вида (13.17) при _k=0 (k=1,2,...,K) и случайных начальных фазах комплексных гармоник _k. Если к данным добавляется белый шум с дисперсией ^, автокорреляционная последовательность выборки {x(n)}, (n=1,2,...,N) может быть записана в виде:

(13.19)

где: P_k - мощность k-ой гармоники, (n) - дельта-функция. Теплицева автокорреляционная матрица размером (N+1)(N+1)

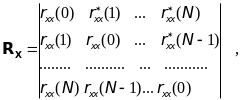(13.20)

имеет структуру:

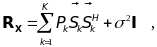(13.21)

где: I - единичная матрица размером (N+1)(N+1), а вектор k-го гармонического сигнала размерности N+1 имеет вид:

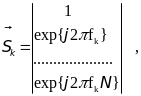(13.22)

Матрица R_X вида (13.21) может быть представлена как сумма автокорреляционной матрицы сигналовSи автокорреляционной матрицы шума Е:

R_X= S + E , (13.23)

причем ранг матрицы

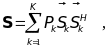(13.24)

равен К, в то время как ранг матрицы Е=²I максимален и равен N+1. Отсюда следует, что разложение матрицы S по собственным значениям можно представить в виде:

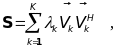(13.25)

где: _k - собственные значения, упорядоченные по степени убывания, а собственные векторы ортонормальны ( ^Н =1; ^Н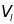 =0 при kl). При этом единичная матрица I может быть представлена так же через ортонормальные собственные векторы как:

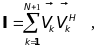(13.26)

откуда после подстановки (13.25) и (13.26) в (13.23) получим:

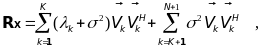(13.27)

Из выражения (13.27) следует возможность разделения матрицы R_X на сигнальное и шумовое подпространства, причем для шумового подпространства все собственные значения равны ² и меньше любого собственного значения сигнального подпространства (_k²). Отсюда вытекает возможность статистически обоснованного разделения оценки автокорреляционной матрицы данных на сигнальное и шумовое подпространства путем анализа ее собственных значений с целью повышения ОСШ и замены в известных методах спектрального оценивания исходной оценки автокорреляционной матрицы ее аппроксимацией пониженного ранга:

. (13.28)

Например, применение подобной процедуры в АРметоде Юла-Уолкера существенно повышает точность и рэлеевское разрешение алгоритма.

Можно показать, что собственные вектора шумового подпространства матрицы R_Xортогональны векторам синусоидальных сигналов. Это дает возможность получать оценки частот гармонических компонент в подпространстве шума (методы Писаренко, собственных векторов и multiplesignalclassification-MUSIC) и строить на их основе псевдооценкиСПМ, которые отражают взаимную относительную интенсивность отдельных гармоник и обладают наивысшим рэлеевским разрешением гармонических сигналов среди параметрических методов спектрального оценивания. Следует заметить, что методы, содержащие процедуру разложения автокорреляционных или близких им по сути матриц по собственным векторам и собственным значениям, с одной стороны, базируются на экспоненциальной или тригонометрической модели и поэтому относятся к параметрическим методам, однако, с другой стороны, используют ортогональное разложение анализируемого сигнала в базисе ортонормированных собственных векторов и поэтому могут быть отнесены к ортогональным методам спектрального анализа.

Основным сдерживающим фактором на пути практического использования данной группы методов является сложность их технической реализации и сравнительно большая трудоемкость вычислений. Кроме того, эти методы, имея в основе гармоническую модель, чувствительны к воздействию окрашенных стохастических сигналов и шумов, что в итоге ухудшает их показатели качества. Это объясняется нарушением адекватности используемой гармонической модели анализируемым сигналам с гладкоокрашенным спектром, которое препятствует эффективному разделению исходной информации, содержащейся в автокорреляционной матрице, на сигнальную и шумовую составляющие.