6.Избранные вопросы теории обнаружения и оценивания параметров сигналов

6.1. Постановка классической задачи обнаружения сигнала

Излучаемый сигнал РЛС s(t)известен полностью и в приемнике имеется его копия. Прямой и отраженный сигнал распространяются в стандартной атмосфере. Принимаемый сигнал может иметь постоянную амплитудуA(модель простой цели в виде единственной блестящей точки) или флуктуирующую амплитуду А(t) (модель сложной цели в виде совокупности блестящих точек). Во втором случае при постановке задачи обнаружения различают два варианта флуктуаций: с простым рэлеевским законом (совокупность равновеликих блестящих точек) и обобщенным рэлеевским законом (присутствие доминирующей блестящей точки в совокупности равновеликих блестящих точек). При этом начальная фаза отраженного целью сигнала является случайной и, как правило, распределена равномерно на интервале [0, 2π].

В простейшем случае обнаружение единственного сигналаs(t) осуществляется на фоне нормального белого шума х(t) с нулевым средним, что обычно соответствует собственным шумам приемника. Принимаемый сигналy(t) может представлять собой либо шум y(t)=х(t), либо аддитивную смесь полезного сигнала и шумаy(t)=s(t)+х(t). При дискретном представлении сигнала (например, при цифровой обработке) непрерывное время tзаменяют на дискретное п. Тогда y(п)=х(п) иy(п)=s(п)+х(п). При этом говорят, что шум х(п) нормальный дельта-коррелированный, т. е., даже соседние отсчеты не коррелированы. В результате анализа принимаемого сигнала y(п) необходимо принять решение: полезный сигнал s(п) на входе приемника отсутствует (гипотеза Н₀) или присутствует (гипотеза Н₁). Возможны четыре события A_ij:

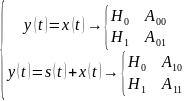(6.1.)

Два из этих событий соответствуют правильным решениям (A₀₀– правильное необнаружение, A₁₁– правильное обнаружение), а два – ложным (A₀₁ - ложная тревога, A₁₀– пропуск цели). Условные вероятности р(A₀₀) и р(A₀₁), а также р(A₁₀) и р(A₁₁) образуют полные группы событий, поэтому их суммы равны 1. Следовательно, для оценки качества обнаружения достаточно использовать одну из вероятностей в каждой группе. Традиционно выбирают р(A₀₁), которойсоответствует вероятность ложной тревоги (ВЛТ) F, и р(A₁₁), которой соответствует вероятность правильного обнаружения (ВПО) D. Заметим, что вероятность правильного необнаружения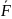 может быть записана как 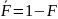. Аналогично вероятность пропуска цели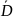 записывается как

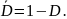
Для оценки качества обнаружения используется критерий минимума байесовского риска или критерий Байеса. По этому критерию каждому событию A_ijприсваивается стоимость (штраф) или риск r_ij. Логично штраф присваивать ошибочным решениям, поэтому общий риск, который необходимо минимизировать, можно записать как:

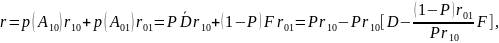(6.2)

где Р – вероятность появления цели в зоне обзора. Это доопытная вероятность, которую мы обычно не знаем. В общем виде байесовский критерий не приводит к конструктивному результату, поэтому переходят к частному варианту - критерию Неймана – Пирсона. Он основан на том, что, хотя доопытная вероятность Р нам неизвестна, но она положительна и постоянна (или фиксирована) при синтезе оптимального правила (алгоритма обработки). Логично предположить, что риски (штрафы) при неправильных решениях также положительны и должны быть зафиксированы. Тогда, в соответствии с вышеприведенной формулой общий риск минимален, если максимально выражение в квадратных скобках:

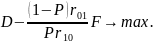(6.3.)

Обозначим

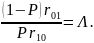(6.4)

Тогда

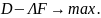(6.5)

Условие оптимизации имеет множество решений, поскольку включает две изменяемые величины – D и F. Критерий Неймана – Пирсона рассматривает частный случай, когда одна из переменных, в данном случае ВЛТF, зафиксирована. Тогда лучший (оптимальный) алгоритм обработки тот, который при равной ВЛТ обеспечивает максимальную ВПОD. Как известно, эти вероятности могут быть определены через свои плотности распределения. Рассмотрим случай дискретного сигнала y(п). Его выборка длиной в N отсчетов позволяет представить анализируемый сигнал как вектор соответствующей размерности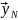 . 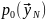Тогда плотности распределения вероятностей и 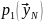при двух альтернативных гипотезах Н₀и Н₁ позволяют определить ВЛТ и ВПО как:

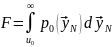(6.6)

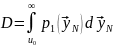(6.7)

Осуществим подстановку:

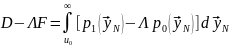(6.8)

Из анализа подынтегрального выражения следует, что интеграл максимален, если он включает в подынтегральном выражении все области, где оно положительно, т.е., ≥0:

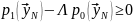, (6.9)

или

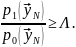(6.10)

Это соотношение называют отношением правдоподобия. Для нахождения конкретного алгоритма обработки необходимо подставить плотности распределения. Для нормального стационарного центрированного процесса, когда сигнал содержит только шум с дисперсией 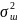, плотность распределения одиночного отсчета:

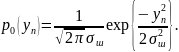(6.11)

При появлении полезного сигнала, отсчеты которого выполняют функцию математического ожидания процесса, плотность распределения одиночного отсчета примет вид:

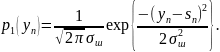(6.12)

Можно графически проиллюстрировать механизм определения вероятностей D и F. На рисунке 6.1 представлено графическое определение ВЛТF как площадь под кривой справа от линии порога y_о при отсутствии полезного сигнала. На рисунке 6.2 аналогично представлено определение ВПОD как площадь под кривой справа от линии порога y_о при наличии полезного сигнала.

Для всей выборки вектора размером N векторная форма плотности распределения имеет вид:

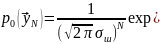(6.13)

и, соответственно, при наличии полезного сигнала:

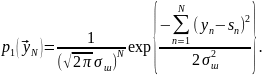(6.14)

Учитывая нормальную плотность вероятности в обоих альтернативных гипотезах, а также монотонную зависимость положительно представленного неравенства, целесообразно вычислять логарифм отношения правдоподобия:

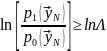. (6.15)

Подставив приведенные плотности вероятностей и выполнив рутинные преобразования, которые приводятся во всех учебниках по теоретическим основам радиолокации, отношение правдоподобия в случае полностью известного сигнала (фиксированные амплитуда и начальная фаза) примет вид корреляционного интеграла:

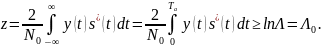(6.16)

Здесь Т_а– время анализа или время существования сигнала, а знак *) означает комплексное сопряжение. При неизвестной равномерно распределенной фазе и фиксированной или случайной амплитуде необходимо вычислять модуль корреляционного интеграла и сравнивать его с порогом:

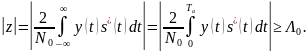(6.17)

Этот случай имеет большое практическое значение и реализуется на практике. Заметим, что логарифмическое преобразование – не единственно возможное, но оно приводит к самой простой процедуре обнаружения сигнала.

Обычно полезный сигнал имеет неизвестную априори задержку 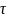, а при когерентной обработке – еще и неизвестный доплеровский сдвиг частоты 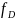. Оба эти параметра являются информативными, подлежащими оцениванию. Оценки неизвестных, но не случайных параметров, основанные на отношении правдоподобия, известны как оценки максимального правдоподобия (ОМП). 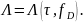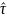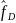Само отношение правдоподобия становится функцией этих параметров: Для получения оценок максимального правдоподобия параметров и в случае нормальной статистики аддитивного шума функцией этих параметров становится модуль корреляционного интеграла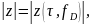 поэтому необходимо вычислять модуль корреляционного интеграла в области возможных значений этих параметров (в рабочей зоне) и находить его абсолютный максимум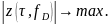 Отсюда следует важный для практики вывод: в случае обнаружения и в случае оценивания (измерения) информативных параметров оптимальный алгоритм обработки остается неизменным и основан на вычислении модуля корреляционного интеграла:

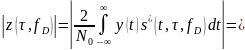
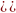(6.17)

В случае обнаружения вычисленное значение модуля корреляционного интеграла сравнивают в пороговом устройстве (ПУ) с порогом 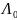, выбираемым исходя из заданной вероятности ложной тревоги F. В случае оценивания параметров в решающем устройстве (РУ) находят абсолютный максимум модуля корреляционного интеграла 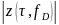как функцию информативных параметров 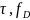в пределах рабочих интервалов их изменений.