Питання для самоперевірки

1. Назвіть основні компоненту кубу.

2. Як визначається розмірність кубу?

3. Як звичайно виглядає структура таблиці фактів?

4. Які типи фактів Ви знаєте?

Методичні вказівки до лекції: [2, с. 40–44] ; [3, с. 80-86]; [5, с. 971–976, 984]; [8,с. 30–32].

Вправи

1. Наведіть приклади вимірів для предметної області «Деканат».

2. Наведіть приклади мір для предметної області «Телефонна компанія».

3. Надайте структуру таблиці фактів для предметної області «Поліклініка».

Лекція №6 Ієрархії вимірів. Схеми кубу «зірка» та «сніжинка»

Розглядаються наступні питання:

• класи параметрів;

• ієрархії вимірів;

• схеми «зірка» і «сніжинка»;

• операції, виконувані над гіперкубом.

Параметри складаються із двох компонентів:

• чисельна характеристика факту, наприклад, ціна або доход від продажів;

• формула, звичайно проста агрегативна функція, наприклад, сума, що може поєднувати кілька значень параметрів в одне.

Параметри, як правило, представляють властивості факту, який користувач хоче вивчити. Параметри приймають різні значення для різних комбінацій вимірів. Чисельна характеристика і формула вибираються таким чином, щоб представляти осмислену величину для всіх комбінацій рівнів агрегування.

Можна визначити три різних класи параметрів за поводженням при обчисленнях.

Аддитивні параметри можуть змістовним образом комбінуватися в будь-якому вимірі. Наприклад, має сенс підсумувати загальний обсяг продажів для продукту, місця розташування й часу, оскільки це не викликає накладення серед явищ реального миру, які генерують кожне із цих значень.

Напіваддитивні параметри, які не можуть комбінуватися в одному або декількох вимірах. Наприклад, підсумовування запасів по різних товарах і складам має сенс, але підсумовування запасів товарів у різний час безглуздо, оскільки той самий фізичний предмет може враховуватися кілька разів.

Неаддитивні параметри не комбінуються в будь-якому вимірі, зазвичай тому, що обрана формула не дозволяє, наприклад, об'єднати середні значення низького рівня в середнім значенні більше високого з.

Аддитивні й неаддитивні параметри можуть описувати факти будь-якого роду, у той час як напіваддитивні параметри, як правило, використаються з миттєвими знімками або сукупними миттєвими знімками.

Виміри організуються в ієрархію, що складається з декількох рівнів, кожний з яких представляє рівень деталізації, необхідний для відповідного аналізу.

Об'єкти у вимірах можуть бути різного типу, наприклад «виробники» - «марки автомобіля» або «роки» - «квартали».

Існують наступні типи ієрархій:

• збалансовані (balanced);

• незбалансовані (unbalanced);

• нерівні (ragged).

Збалансована ієрархія – ієрархія, у якій число рівнів визначене її структурою й незмінно, і кожна галузь ієрархічного дерева містить об'єкти кожного з рівнів.

К

Рис.3. Приклад збалансованої ієрархії

ожному виробникові автомобілів може відповідати кілька марок автомобілів, а кожній марці – кілька моделей автомобілів, тому можна говорити про трьохрівневу ієрархію цих об'єктів. У цьому випадку на першому рівні ієрархії розташовуються виробники, на другому – марки, а на третьому – моделі.

Для формування збалансованої ієрархії необхідна наявність зв'язку «один-до-багатьох» між об'єктами менш детального рівня стосовно об'єктів більш детального рівня.

У принципі кожний рівень збалансованої ієрархії можна представити як окремий простий вимір, але тоді ці виміри виявляться залежними, а виходить, неминуче підвищення розрідженості куба.

Незбалансована ієрархія – ієрархія, у якій число рівнів може бути змінено, і кожна галузь ієрархічного дерева може містити об'єкти, що належать не всім рівням, тільки декільком першим.

В

Рис.4. Приклад незбалансованої ієрархії

сі об'єкти незбалансованої ієрархії належать одному типу.

Типовий приклад незбалансованої ієрархії – ієрархія типу «начальник-підлеглий», де всі об'єкти мають той самий тип –«Співробітник».

Нерівна ієрархія - ієрархія, у якій число рівнів визначене її структурою й постійно, однак на відміну від збалансованої ієрархії деякі гілки ієрархічного дерева можуть не містити об'єкти якого-небудь рівня.

І

Рис.5. Приклад нерівної ієрархії

єрархії такого виду містять такі члени, логічні «батьки» яких не перебувають на безпосередньо вищестоящому рівні.

Типовим прикладом є географічна ієрархія, у якій є рівні «Країни», «Штати» і «Міста», але при цьому в наборі даних є країни, що не мають штатів або регіонів між рівнями «Країни» і «Міста».

Може бути визначено кілька ієрархій для виміру.

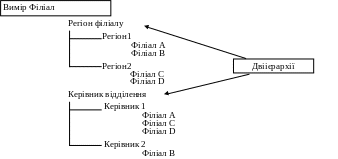
Рис.6. Приклад множини ієрархій для одного виміру

Один вимір куба може втримуватися як в одній таблиці, так і в декількох зв'язаних таблицях, що відповідають різним рівням ієрархії у вимірі. Якщо кожний вимір міститься в одній таблиці, така схема сховища даних зветься «зірка».

Якщо ж хоча б один вимір міститься в декількох зв'язаних таблицях, така схема сховища даних зветься «сніжинка».

Рис.7. Приклад схеми «зірка»

Особливості схеми «зірка»:

1. Одна таблиця фактів, що сильно денормалізована. Є центральною в схемі, може складатися з мільйонів рядків і містить агреговані або фактичні дані, за допомогою яких можна відповісти на різні питання. Кілька денормалізованих таблиць вимірів. Мають меншу кількість рядків, ніж таблиці фактів, і містять описову інформацію. Ці таблиці дозволяють користувачеві швидко переходити від таблиці фактів до додаткової інформації. Кількість рівнів в ієрархії дорівнює кількості стовпців таблиці виміру.

2. Таблиця фактів і таблиці вимірів пов'язані з допомогою зовнішніх ключів. Первинний ключ таблиці факту цілком складається з первинних ключів всіх таблиць розмірності.

3. Агреговані дані зберігаються разом з вхідними.

Переваги схеми «зірка»:

Завдяки денормалізації таблиць вимірів спрощується сприйняття структури даних користувачем і формулювання запитів, зменшується кількість операцій з'єднання таблиць при обробці запитів.

Недоліки схеми «зірка»:

Денормалізація таблиць вимірів вносить надмірність даних, зростає необхідний для їхнього зберігання обсяг пам'яті. Якщо агрегати зберігаються разом з вхідними даними, то у вимірах необхідно використовувати додатковий параметр – рівень ієрархії.

Особливості схеми «сніжинка»

1. Одна таблиця фактів, що сильно денормалізована. Є центральною в схемі, може складатися з мільйонів рядків і містити агреговані або фактичні дані, за допомогою яких можна відповісти на різні питання.

2. Кілька таблиць вимірів, які нормалізовані на відміну від схеми «зірка». Ці таблиці дозволяють користувачеві швидко переходити від таблиці фактів до додаткової інформації. Первинні ключі в них складаються з єдиного атрибута (відповідають єдиному елементу виміру). Елементи різних рівнів ієрархії витягають із декількох таблиць, зв'язаних зовнішніми ключами.

3. Таблиця фактів і таблиці розмірності пов'язані з допомогою зовнішніх ключів. Первинний ключ таблиці факту цілком складається з первинних ключів всіх таблиць розмірності.

4. У схемі «сніжинка» агреговані дані можуть зберігатися окремо від вихідних даних./

Рис.8. Приклад схеми «сніжинка»

Переваги схеми «сніжинка»

Нормалізація таблиць вимірів на відміну від схеми «зірка» дозволяє мінімізувати надмірність даних і більш ефективно виконувати запити, зв'язані зі структурою значень вимірів.

Недоліки схеми «сніжинка»

За нормалізацію таблиць вимірів іноді доводиться платити часом виконання запитів.

Для представлення даних, що зберігаються в кубі, застосовуються, як правило, звичні двовимірні, тобто табличні, представлення, що мають складні ієрархічні заголовки рядків і стовпців. Двовимірне представлення куба можна одержати, "розрізавши" його поперек однієї або декількох осей (вимірів), у цьому випадку фіксуються значення всіх вимірів, крім двох, тобто виходить звичайна двовимірна таблиця. У горизонтальній осі таблиці (заголовки стовпців) представлено один вимір, у вертикальній (заголовки рядків) – інше, а в комірках таблиці – значення мер. При цьому набір мер фактично розглядається як один з вимірів – вибирається для показу або одна міра (і тоді можна розмістити в заголовках рядків і стовпців два виміри), або показується кілька мір (і тоді одну з осей таблиці займуть назви мір, а іншу - значення єдиного «нерозрізаного» виміру).

На рис. 9 зображені різні варіанти двовимірного представлення куба:

1. двовимірний зріз куба для однієї міри Продано штук і двох «нерозрізаних» вимірів – Місце продажу й Час;

2. один «нерозрізане» вимір – Місце продажу, але відображаються значення декількох мер – Продано штук, Сума продажу й Накладні витрати;

3. двовимірне представлення куба, коли «нерозрізаними» залишається більше двох вимірів. При цьому на осях зрізу (рядках і стовпцях) будуть розміщені два або більше виміри куба, що «розріжеться».

а) Двовимірний зріз куба для однієї міри

	Україна	Росія	Польща
Січень	20000	4000	3000
Лютий	30000	6000	3000
Березень	50000	10000	5000

b)Двовимірний зріз куба для декількох мір

	Україна	Росія	Польща
Продано штук	20000	4000	3000
Сума продажу	30000	6000	3000
Накладні витрати	50000	10000	5000

с) Двовимірний зріз куба з декількома вимірами на одній осі

	Січень			Лютий
	Україна	Росія	Польща	Україна	Росія	Польща
Продано штук	500	100	50	5000	300	200
Сума продажу	7500	…
Накладні витрати

Рис.9 Різні варіанти двовимірного представлення куба

Операції, виконувані над гіперкубом

1. Зріз (slice-and-dice) – формується підмножина багатомірного масиву даних, що відповідає єдиному значенню одного або декількох елементів вимірів, що не входять у цю підмножину.

Приклад. Якщо обмежиться значенням виміру Модель Комп'ютера - Celeron, то вийде підмножина гіперкуба (у цьому випадку – двомірна таблиця), що містить інформацію про історію продажів цієї моделі різними менеджерами в різні роки.

2. Обертання (rotating) – зміна розташування вимірів, представлених у звіті або на відображуваній сторінці. Наприклад, операція обертання може полягати в перестановці місцями рядків і стовпців таблиці. Крім того, обертанням куба даних є переміщення позатабличних вимірів на місце вимірів, представлених на відображуваній сторінці, і навпаки.

Приклад для першого випадку.Є звіт, для якого елементи виміру "Час" розташовуються поперек екрана (заголовки стовпців таблиці), а елементи виміру «Комп'ютери» – уздовж екрана (заголовки рядків таблиці). Після застосування операції обертання звіт буде мати такий вигляд: елементи виміру «Комп'ютери» будуть розташовані по горизонталі, а елементи виміру «Час» – по вертикалі.

3. Консолідація (roll-up) і деталізація (drill-down) – операції, які визначають перехід нагору по напрямку від детального представлення даних до агрегованого й навпаки, відповідно. Напрямок деталізації (узагальнення) може бути заданий як по ієрархії окремих вимірів, так і згідно іншим відношенням, установленим у рамках вимірів або між вимірами.

Приклад.Проаналізувавши, наскільки успішно в 2010 р. Петров продавав моделі Pentium і Athlon, директор може захотіти довідатися, як виглядає співвідношення продажів цих моделей на рівні Підрозділу, де Петров працює. А потім одержати аналогічну довідку по Регіоні або Фірмі.

4. Злиття (drill-across) комбінує куби, які мають одне або кілька загальних вимірів. З погляду реляційної алгебри така операція виконує з'єднання (join).

5. Ранжирування (ranking) повертає тільки ті комірки, які з'являються у верхній або нижній частині впорядкованого певним чином списку, наприклад, 10 самих продаваних продуктів у конкретному місті в 2009 році.