Ргз №1 «Приложения дифференциального исчисления функций одной переменной»

Вариант 5

Задача 1

Найти наибольшее и наименьшее значения функции на замкнутом промежутке, построив ее график на этом промежутке, если , .

Задача 2

Провести полное исследование свойств следующих функции и построить их графики:

1) ; 2) ; 3) ; 4) .

Задача 3 (Берман, №1218)

Из круга фиксированного радиуса R вырезан сектор с центральным углом . Из сектора свернута коническая поверхность. При каком значении угла объем полученного конуса будет наибольшим?

Задача 4 (Берман, №901)

Используя равенство , вычислить приближенно .

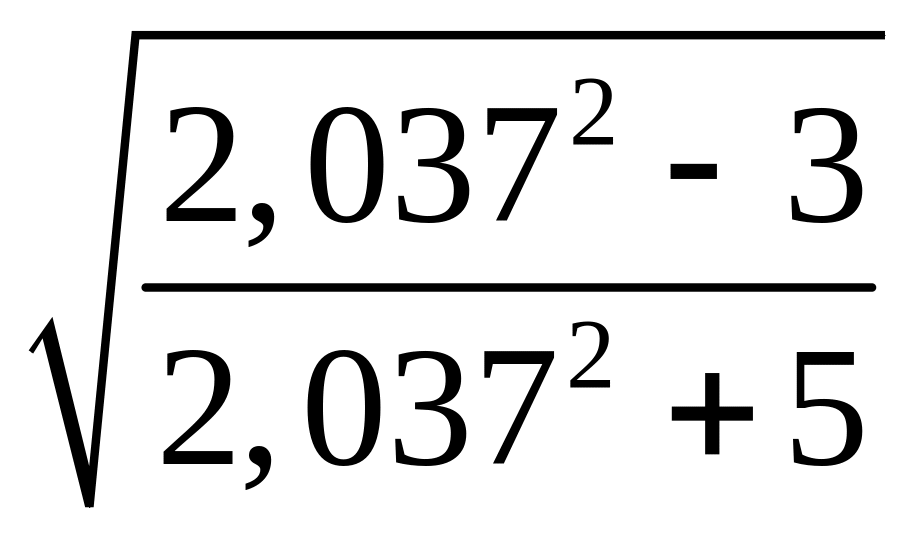Задача 5 (Берман, №820)

Тело массой 3 кг движется прямолинейно по закону ; расстояние s выражено в сантиметрах, время t – в секундах. Определить кинетическую энергию тела через 5 с после начала движения.

Задача 6

Д ан график функции .

Н айти: 1) ;

2) , , ;

3) промежутки монотонности функции;

4) уравнения асимптот;

5) значения , для которых ;

6) , ;

7)локальные экстремумы функции;

8) значение .

Специальность 09.03.01 «ИВТ»

дисц. Математический анализ

Ргз №1 «Приложения дифференциального исчисления функций одной переменной»

Вариант 6

Задача 1

Найти наибольшее и наименьшее значения функции на замкнутом промежутке, построив ее график на этом промежутке, если , .

Задача 2

Провести полное исследование свойств следующих функции и построить их графики:

1) ; 2) ; 3) ; 4) .

Задача 3 (Берман, №1231)

Найти высоту прямого кругового конуса наименьшего объема, описанного около шара фиксированного радиуса R.

Задача 4

Используя равенство , вычислить приближенно .

Задача 5 (Берман, №1001)

Поезд и воздушный шар отправляются в один и тот же момент из одного пункта. Поезд движется равномерно со скоростью 50 км/ч, шар поднимается (тоже равномерно) со скоростью 10 км/ч. С какой скоростью они удаляются друг от друга? Как направлен вектор скорости?

Задача 6

Д ан график функции :

Найти: 1) значение ;

2) , , ;

3) значение ;

4) уравнения асимптот;

5) значения , для которых ;

6) , ;

7) значения , для которых выполняются

три условия , и ;

8) количество локальных экстремумов

функции.

Специальность 09.03.01 «ИВТ»

дисц. Математический анализ