
- •«Мурманский государственный технический университет»
- •Методические указания к выполнению расчетно-графического задания
- •Оглавление
- •1. Общие организационно-методические указания
- •2. Задание, план выполнения, требования к оформлению
- •Содержание задач каждого варианта:
- •Общие требования к оформлению ргз:
- •План выполнения ргз:
- •3. Список рекомендуемых источников
- •5. Пример выполнения заданий ргз Задача 1
- •Задача 2
- •Задача 3
- •Задача 4
- •Задача 5
- •Задача 6
- •Приложение а. Образец оформления титульного листа
- •Расчетно-графическое задание
- •Приложение б. Варианты заданий
- •Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
- •Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
- •Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
- •Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
- •Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
- •Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
- •Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
- •Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
- •Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
- •Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
- •Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
- •Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
- •Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
- •Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
- •Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
- •Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
- •Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
- •Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
- •Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
- •Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
- •Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
- •Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
- •Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
Задача 6
По данному графику функции ответить на следующие вопросы:
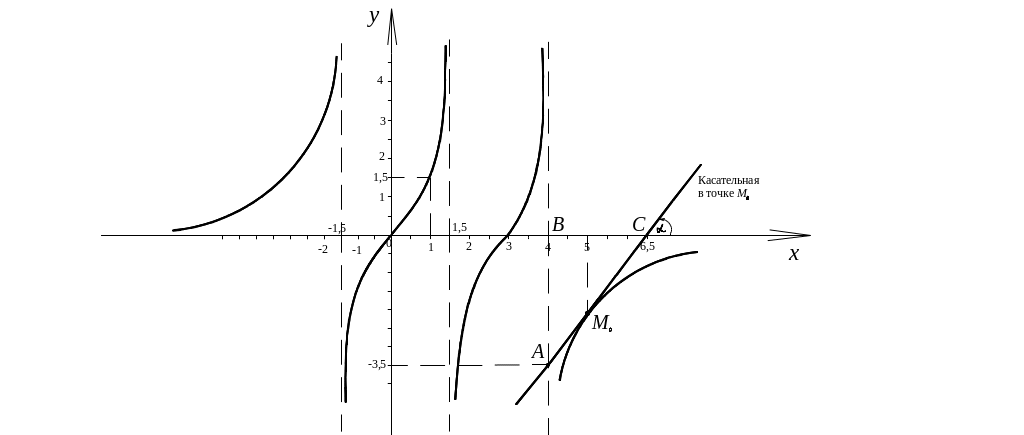
1) чему равно значение ?
2) чему равны пределы:
![]() ,
,
![]() ,
?
,
?
3) запишите промежутки изменения аргумента, на которых выполняются три условия
4) чему равны пределы: , , ?
5) запишите нули функции;
6) запишите уравнения асимптот;
7) запишите промежутки знакопостоянства и ;
8) чему равно значение ?
Ответы:
 ;
;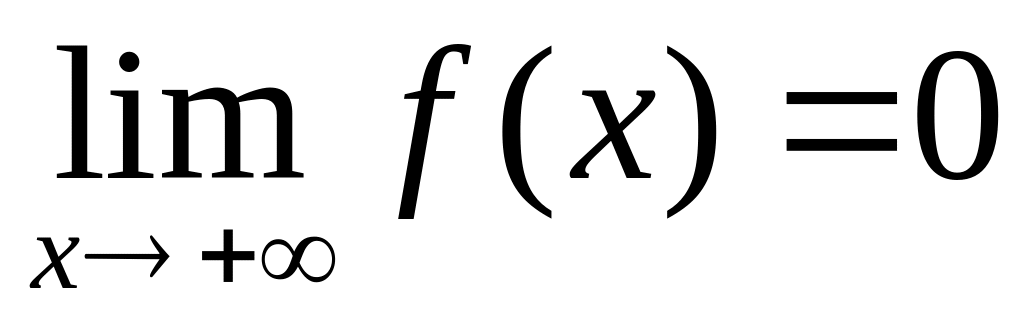 ,
,
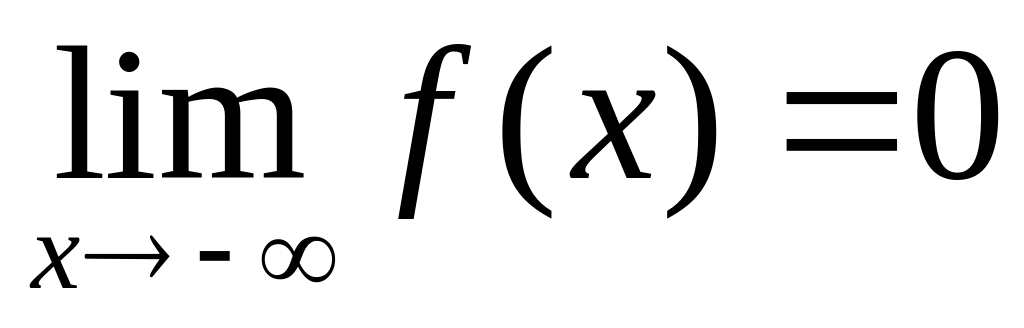 ,
,
 ;
;на промежутках
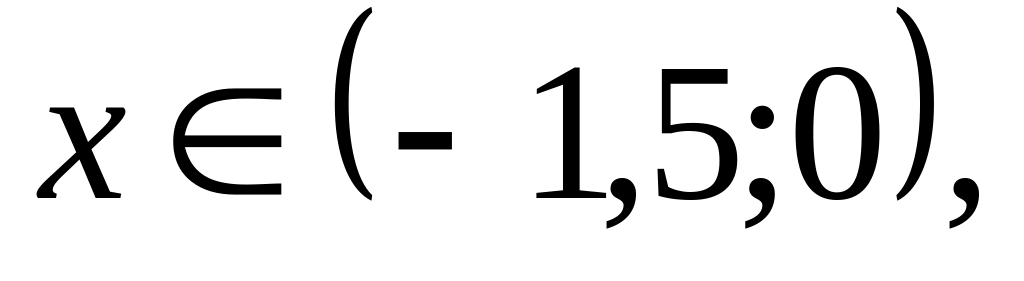

 выполняются три условия:
выполняются три условия:
![]()
 ,
,
 ,
,
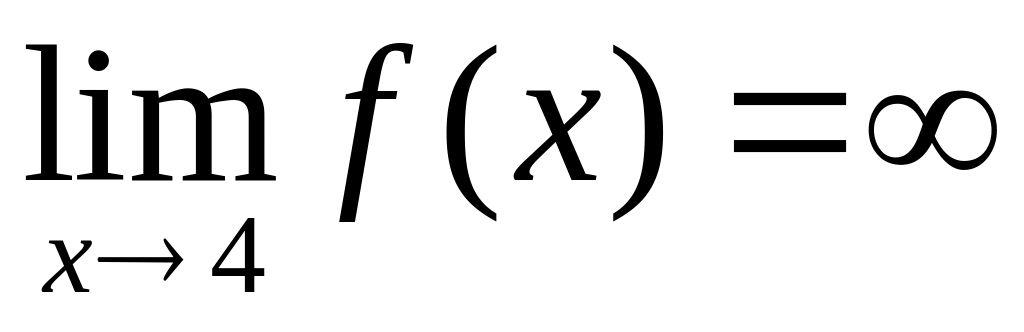 ;
;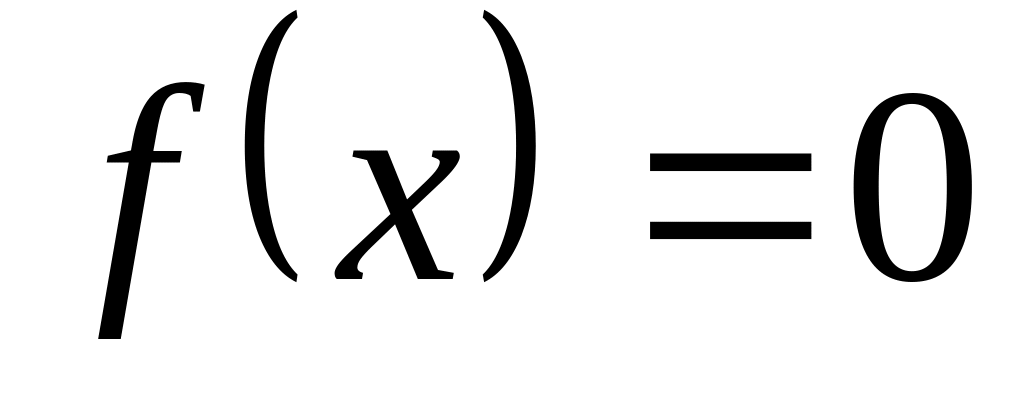 в точках x = 0 и x
= 3;
в точках x = 0 и x
= 3;уравнения асимптот: x = -1,5; x = 1,5; x = 4 – это уравнения вертикальных асимптот;
y = 0 – уравнение
горизонтальной асимптоты при
![]() ;
;
промежутки знакопостоянства первой и второй производных:
![]() при
при
![]() ;
;
![]() – таких промежутков нет;
– таких промежутков нет;
![]() при
при
![]() ;
;
![]() при
при
![]() ;
;
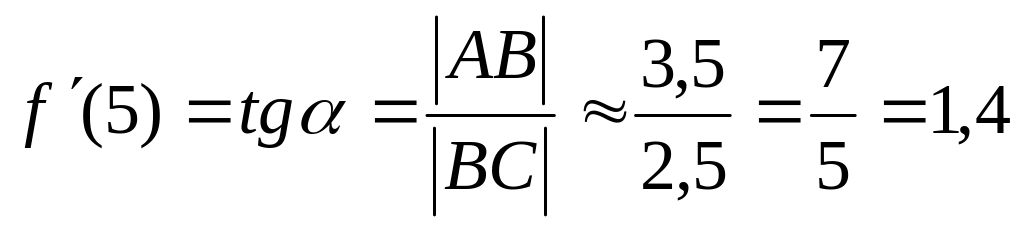 .
.
Приложение а. Образец оформления титульного листа
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО РЫБОЛОВСТВУ
ФГБОУ ВПО «Мурманский государственный технический университет»
Кафедра Математики, информационных технологий и ПО
Расчетно-графическое задание
«Приложения дифференциального исчисления функций одной переменной»
по дисциплине «Математический анализ»
выполнил: студентка группы ИВТ-111
Осетрова Т.
проверил: доцент Кацуба В.С.
оценка: _____________________
дата: _____________________
Мурманск,
2016
Приложение б. Варианты заданий
Специальность 09.03.01 «ИВТ»
дисц. Математический анализ
РГЗ №1 «Приложения дифференциального исчисления функций одной переменной»
Вариант 1
Задача 1
Найти наибольшее и наименьшее значения
функции
![]() на замкнутом промежутке, построив ее
график на этом промежутке, если
на замкнутом промежутке, построив ее
график на этом промежутке, если
![]() .
.
Задача 2
Провести полное исследование свойств функции и построить график:
1)![]() ; 2)
; 2)![]() ; 3)
; 3)
![]() ; 4)
; 4)
![]() .
.
Задача 3 (Берман, №1252)
На странице книги печатный текст должен занимать S квадратных сантиметров. Верхнее и нижнее поля должны быть по а см, правое и левое поле – по b см. Если принимать во внимание только экономию бумаги, то какими должны быть наиболее выгодные размеры страницы?
Задача 4
Используя равенство
![]() ,
вычислить приближенно
,
вычислить приближенно
![]() .
.
Задача 5 (Берман, №822)
Колесо вращается так, что угол поворота
пропорционален квадрату времени. Первый
оборот был сделан колесом за 8 секунд.
Найти угловую скорость
![]() через 32 секунды после начала движения?
через 32 секунды после начала движения?
Задача 6
Д ан
график функции. Найти:
ан
график функции. Найти:
1) значение f(3);
2) , ;
3) локальные экстремумы функции;
4) значения x, для которых выполняются
три условия:
![]() ;
;
5) значения x, для которых f(x) = 4;
6) значение
![]() ;
;
7) уравнения асимптот;
8) промежутки знакопостоянства
![]() .
.
Специальность 09.03.01 «ИВТ»
дисц. Математический анализ
РГЗ №1 «Приложения дифференциального исчисления функций одной переменной»
Вариант 2
Задача 1
Найти наибольшее и наименьшее значения
функции
на замкнутом промежутке, построив ее
график на этом промежутке, если
![]() ,
,
![]() .
.
Задача 2
Провести полное исследование свойств следующих функции и построить их графики:
1)
![]() ;
2)
;
2)
![]() ; 3)
; 3)
![]() ;
4)
;
4)
![]() .
.
Задача 3 (Берман, №1221)
Найти высоту цилиндра наибольшего объема, который можно вписать в шар фиксированного радиуса R.
З адача
4
адача
4
Используя равенство
,
вычислить приближенно
![]() .
.
Задача 5 (Берман, №1084)
Тяжелую балку длиной 13 м спускают на землю так, что нижний конец прикреплен к вагонетке, а верхний удерживается канатом, намотанным на ворот. Канат сматывается со скоростью 2 м/мин. С каким ускорением откатывается вагонетка в момент, когда она находится на расстоянии 5 м от точки О (рис.1)?
Задача 6
Дан график функции .
Н айти:
айти:
1) промежутки непрерывности функции;
2) значения![]() ,
для которых выполняются одновременно
условия
,
для которых выполняются одновременно
условия
![]() ,
,
![]() ,
,
![]() ;
;
3) значения
,
для которых
![]() ;
;
4) значение
![]() ;
;
5)
![]() ,
,
![]() ,
,
![]() ;
;
6)
![]() ,
,
![]() ;
;
7) экстремумы функции.
8) промежутки знакопостоянства
![]() .
.
Специальность 09.03.01 «ИВТ»
дисц. Математический анализ
