Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
Вариант 15
Задача 1
Найти наибольшее и наименьшее значения функции на замкнутом промежутке, построив ее график на этом промежутке, если , .
Задача 2
Провести полное исследование свойств следующих функции и построить их графики:
1) ; 2) ; 3) ; 4) .
Задача 3 (Берман, №1234)
Найти высоту конуса наименьшего объема, описанного около полушара фиксированного радиуса R (центр основания конуса лежит в центре шара).
Задача 4
Используя равенство
,
вычислить приближенно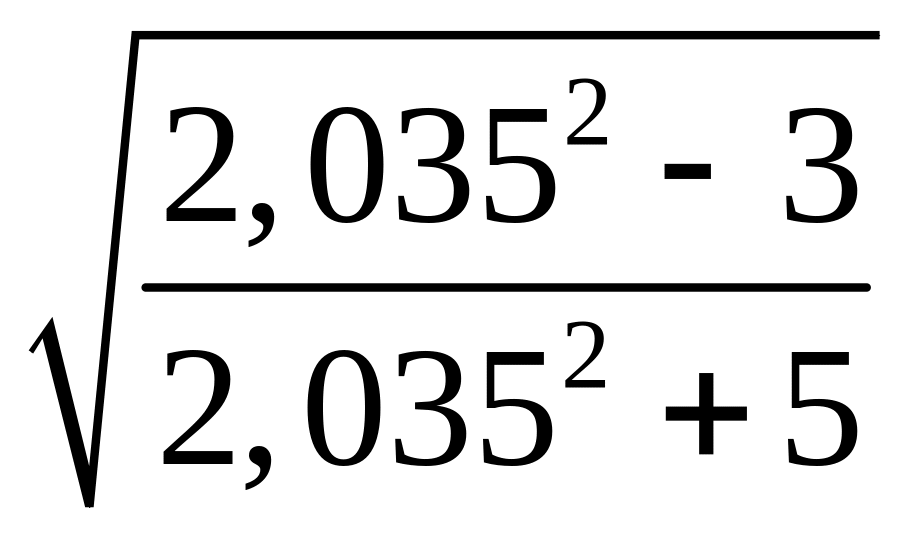
.
Задача 5 (Берман, №923)
Ордината точки, описывающей окружность , убывает со скоростью 1,5см/с . С какой скоростью изменяется абсцисса точки, когда ордината становится равной 4см?
Задача 6
Д ан график функции :
Н айти:
1) значение ;
2) уравнение наклонной асимптоты;
3) значение
;
4) значения , для которых выполняются три
условия:
,
,
;
5)
,
;
6) локальные экстремумы функции;
7) значения , для которых ;
8) промежутки знакопостоянства .
Специальность 09.03.01 «ИВТ»
дисц. Математический анализ
Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
Вариант 16
Задача 1
Найти наибольшее и наименьшее значения функции на замкнутом промежутке, построив ее график на этом промежутке, если , .
Задача 2
Провести полное исследование свойств следующих функции и построить их графики:
1)
;
2)
;
3)
; 4)
.
Задача 3 (Берман, №1227)
На окружности дана точка А. Составить уравнение хорды ВС, параллельной касательной в точке А, так чтобы площадь треугольника АВС была наибольшей.
Задача 4
Используя равенство
,
вычислить приближенно
.
Задача 5 (Берман, №824)
Количество электричества, протекшее через проводник, начиная с момента времени , дается формулой (Кл). Найти силу тока в конце пятой секунды?
Задача 6
Д ан график функции :
Найти:
1) значения
;
2) , ;
3) локальные экстремумы функции;
4) значения , для которых выполняются
три условия: , , ;
5) значения , для которых ;
6) уравнения асимптот;
7) значение ;
8) промежутки знакопостоянства .
Специальность 09.03.01 «ИВТ»
дисц. Математический анализ
Ргз №1 «Приложения дифференциального исчисления функций одной переменной»
Вариант 17
Задача 1
Найти наибольшее и наименьшее значения функции на замкнутом промежутке, построив ее график на этом промежутке, если , .
Задача 2
Провести полное исследование свойств следующих функции и построить их графики:
1)
; 2)
; 3)
; 4)
.
Задача 3 (Берман, №1232)
Найти угол при вершине осевого сечения конуса наименьшей боковой поверхности, описанного около шара фиксированного радиуса R.
Задача 4
Используя равенство
,
вычислить приближенно
.
Задача 5 (Берман, №432)
Имеется тонкий неоднородный стержень . Длина его см. Масса отрезка растет пропорционально квадрату расстояния точки M от точки A, причем известно, что масса отрезка см равна 8 г. Найти: а) среднюю линейную плотность отрезка стержня см; б) среднюю линейную плотность всего стержня; в) плотность стержня в точке M.
Задача 6
Д ан график функции :
Найти: 1) значение
;
2)
,
;
3) значение ;
4) уравнения асимптот;
5) значения
,
для которых
;
6) , ;
7) значения , для которых выполняются
три условия , и .
8) значения , для которых существует.
Специальность 09.03.01 «ИВТ»
дисц. Математический анализ