2. Неразрезной ригель

Назначаем предварительные размеры поперечного сечения ри­геля.

Высота сечения h=(1/10...1/12)l=(1/10...1/12)6300= 600.

Ширина сече­ния ригеля b= (0,3 ... 0,4)h= 250 мм.

Вычисляем расчетную нагрузку на 1 м длины ригеля. Нагрузка на ригеле от многопустотных плит считается равномерно распределенной. Ширина гру­зовой полосы на ригель равна шагу колонн в продольном направлении здания 5.8м. Подсчет нагрузок на 1 м перекрытия приведен в таблице 1.

Постоянная нагрузка на ригель будет равна:

• от перекрытия (с учетом коэффициента надежности по классу сооружения γ_n = 1.1)

g_пер=g*L₁* γ_n =4,62· 5,8·1,1=29.47 кН/м;

• от веса ригеля (сечение 0,25 × 0,65 м, плотность железобетона р =25 кН/м , с учетом коэффициентов надежности γ_f=1,1 и у_п =1,1),

g_p=B*h*ρ*γ_n* γ_f= 0,25·0,6·25·1,1·1,1=4,53кН/м.

Итого: g= g_пер + g_p =29,47+4,53=34кН/м.

Временная нагрузка (с учетом γ_п=1,1)

υ_p=L₁*υ* γ_п =9 · 5,8· 1,1=57,42 кН/м.

Полная нагрузка q= g+v= 34+57,42=91,42 кН/м.

1. Расчет прочности ригеля по сечениям, нормальным к продольной оси.

Уточнённые размеры сечения ригеля 0.25х0.6м.

Сечение в пролете, М=333,2кН·м, h₀=600 - 60 =540 мм. Подбор продольной арматуры производим согласно п. 3.21 [7].

Вычисляем α_m = М/(R_b·b·h₀²) =333,2·10⁶/(17·250·540²)=0,268<α_r=0,391

Требуемую площадь арматуры вычислим по формуле:

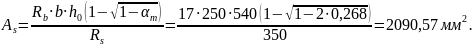
Принимаем 6Ø22 A400 (A_s= 2281 мм²).

Сечение на опоре М =227 кН·м, h₀ =600-45 =555 мм

α_m= 227·10⁶/(17·250·555²) = 0.173< α_r= 0.391

Принимаем 3Ø25 A400 (A_s= 1473 мм²).

Монтажную арматуру принимаем 3Ø12 A400 (A_s= 339 мм²)

Расчет прочности ригеля по сечениям, наклонным к продольной оси

Q_max=310,8 кН, q₁= q= 91,42 кН/м (Н/мм).

Определим требуемую интенсивность поперечных стержней согласно п. 3.33, б [7], принимая в опорном сечении h₀=567 мм. (а=22+22/2=33→ h₀= h-а=600-33=567мм)

M_b=1,5 R_bt b h₀² = 1,5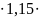 250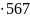 ² = 138,64 кН м

Находим Q_b1

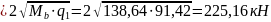
Поскольку Q_b1>2M_b/h₀-Q_max=2 138.64/0.567-310.8=178.22кН, то требуемую интенсивность поперечных стержней q_swопределяем по формуле (3.52)[7], так как

Q_b1>R_btbh₀ =0,9 250 612=137812,5 кН

,

При этом соблюдается условие(3.49) [7]:

По условию сварки принимаем поперечные стержни Ø8 класса В500(R_sw=300 МПа); при трех каркасах в расчетном сечении получим А_sw = 151 мм² ; требуемый по расчету шаг поперечных стержней должен быть равен:

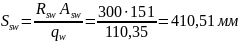
Согласно п. 5.21 [7] шаг поперечных стержней у опоры должен быть не бо­лее

0,5h₀= 0,5·567 = 283,5 мм и не более 300 мм. Максимально допустимый шаг поперечных стержней вычисляем по формуле (3.60)[7]:

мм

Принимаем шаг поперечных стержней у опоры s_w1= 270мм, удовлетво­ряющий расчетным и конструктивным требованиям с фактической интенсивностью поперечных стержней вычисляем по формуле (3.60)[7]:

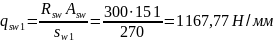
Шаг поперечных стержней в пролете ригеля должен быть не более

0,75h₀= 0,75·567 = 425,25 мм и не более 500 мм. Принимаем шаг поперечных стержней в пролете s_w2 =420 мм, удовлетворяющий конструктивным требова­ниям с фактической интенсивностью поперечных стержней:

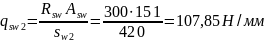
Для определения минимальной длины участка ригеля с интенсивностью поперечных стержней q_sw2в соответствии с п. 3.34[7] находим

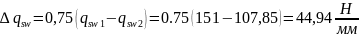
Так как 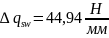<q₁ = 91,42Н/мм, то величину l₁вычисляем по формуле (3.58)[7]:

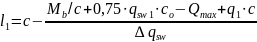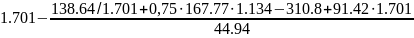= =0.168м

где 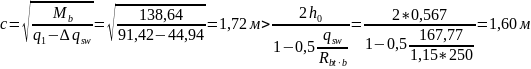но поскольку c = 1,72м 3h₀= 3·0,567 =1,701, принимаем c = 1,701м; с учетом условия с₀= с, но не более 2 h₀, принимаем с₀= 2·0,567 = 1,134м.

При конструировании ригеля фактическая длина l₁принимается с учетом длины обрываемых стержней продольной рабочей арматуры.

Проверяем прочность наклонной полосы между наклонными трещинами по условию (3.43) [7]:

0,3R_bbh₀=0,3·17·250·567=729,925кH>Q_max=310,8 кН, следовательно, прочность и наклонной полосы обеспечена.

Построение эпюры материалов выполняем с целью рационального конст­руирования продольной арматуры ригеля в соответствии с огибающей эпюрой изгибающих моментов.

Определяем изгибающие моменты, воспринимаемые в расчетных сечени­ях, по фактически принятой арматуре.

Сечение в пролете с продольной арматурой 3Ø22 А400, A_s= 1140 мм²;

x=R_sA_s/(R_bb) =350·1140/(17·250) = 93,88мм, ξ=x/h₀=93,88/567=0,165<ξ_R=0,533;тогда

M_ult=R_sA_s(h₀-0,5x)=350 · 1140(567- 0,5·93,88)=207,5· 10⁶Н·мм = 207,5кН·м

Сечение в пролете с продольной арматурой 6Ø22А400,As=2281 мм²;

x = 350·2281/(17·250) = 187,84мм, ξ = 187,84/537 = 0,349 ξ_R= 0,533;

тогда M_ult=350·2281(537- 0,5·187,84) = 353.7·10⁶Н·мм =353.7кН·м.

Сечение в пролете с конструктивной арматурой в верхней зоне 3Ø12А400, A_s= 339 мм²;

x = 350·339/(17·250) = 27,9.мм,

тогда M_ult=350·226(562 - 0,5·27,9)=65.02· 10⁶Н·мм = 65.02кН·м.

Сечение у опоры с арматурой в верхней зоне 3Ø25А400, A_s=1473мм²;

x=350·1473 / (17·250)=121.3мм, ξ =121.3/562=0,215<ξr=0,533;

тогда M_ult=350·1473(562 - 0,5·121.3)= 258.5·10⁶Н·мм = 258.5 кН·м.

Пользуясь полученными значениями изгибающих моментов, графическим способом находим точки теоретического обрыва стержней и соответствующие им значения поперечных сил.

Вычисляем необходимую длину заведения обрываемых стержней за точки теоретического обрыва для обеспечения прочности наклонных сечений на дей­ствие изгибающих моментов согласно п. 3.47 [7].

Для нижней арматуры по эпюре Q_maxграфическим способом находим по­перечную силу в точке теоретического обрыва стержней Ø22мм Q= 150.4кН.

Поскольку 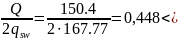h₀=0,567м

Длину заведения обрываемых стержней за точки теоретического обрыва вычисляем по формуле (3.79)[7]:

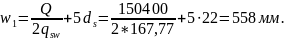
Для верхней арматурыØ25 мм у опоры по эпюре Q_min= 108,5 кН.

Длину заведения обрываемых стержней за точки теоретического обрыва вычисляем по формуле (3.79)[7]: