2. Расчет плиты по предельным состояниям второй группы

Согласно требованиям п. 8.2.6 [5], представленным в таблице IV.4 приложения IV, в плите, армированной напрягаемой арматурой класса А1000 диаметром 9 мм, допускается предельная ширина продолжительного раскрытия трещин a_crc,_uit= 0,2 мм и непродолжительного - a_crc,ult= 0,3 мм.

По таблице Е.1 поз. 2 [12] для расчетного пролета 5,575 м относительное значение предельного прогиба из эстетико-психологических требований равно

1/150-(1/150- 1/200)·(5,675 - 3)/(6 - 3) = 0,00518, и следовательно, величина пре­дельного прогиба составляет f_ult= 0,00513 · 5675 = 29.39 мм.

Геометрические характеристики приведенного сечения плиты, рассчитан­ные ЭВМ, имеют следующие значения:

• площадь бетонного сечения A= 0.2279·10⁶ мм²;

• площадь приведенного сечения A_red= 0.2325·10⁶ мм²;

• статический момент приведенного сечения S_red= 0.2521·10⁸ мм ;

• расстояние от нижней грани до центра тяжести приведенного сечения у = 108,4 мм;

• момент инерции приведенного сечения I_red= 0.1472·10¹⁰ мм⁴;

• момент сопротивления приведенного сечения W_red= 0.1358·10⁸ мм ;

• расстояние от центра тяжести приведенного сечения до верхней ядровой точки r=58.4 мм;

Назначаем передаточную прочность бетона R_bp=25 МПа, удовлетво­ряющую требованиям п. 6.1.6 [5].

3. Определим потери предварительных напряжений

Потери от релаксации напряжений в арматуре согласно п.9.1.3 [5] равны

Δσ_sp1 =(0,22 - 0.1) σ_sp =(0,22*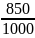 - 0.1) 850 = 73,95 МПа.

Потери от температурного перепада при электротермическом способе натяжения арматуры на упоры формы отсутствуют, так как форма нагреваетсявместе с изделием, т.е.

Δσ_sp2 = 0

При электротермическом способе натяжения арматуры потери Δσ_sp3 = 0 иΔσ_sp4= 0.

Полные значения первых потерь предварительного напряжения арматуры находим по формуле:

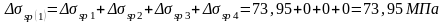
Тогда усилие обжатия с учетом первых потерь будет равно:

A_sp(σ_sp- 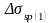)=785*(850-73.95)=609.2kH.

В связи с отсутствием в верхней зоне напрягаемой арматуры эксцентриситет усилия обжатия относительно центра тяжести приведенного сечения будет равен 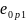=y-a_p=108.4-30=78.4мм.

Проверим максимальное сжимающее напряжение в бетоне 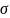_bpот действия усилия P₍₁₎ , вычисляя _bpпо формуле (9.14)[5] при y_s= y =108,4 мм и принимая изгибающий момент от собственного веса плиты равным нулю:

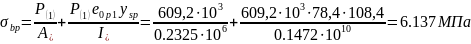<0.9 _Rbp =0.9*25=22.5 т.е. требование п. 9.1.11 [5] выполняется.

Определим вторые потери напряжений согласно пп.9.1.8 и 9.1.9 [5].

Потери от усадки равны

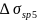=ε_b,_shE_s=0,0002·200000=40 МПа,

где ε_b,_sh=0,0002 -деформация усадки бетона классов В35 и ниже.

С учетом тепловой обработки бетона при атмосферном давлении (по заданию) необходимо умножить полученный результат на коэффициент 0,85. Тогда окончательно получим =40*0,85=34Мпа.

Для нахождения потерь от ползучести бетона вычислим напряжение в бе­тоне 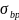в середине пролета балки от действия силы P₍₁₎и изгибающего момента M_wот массы плиты.

Нагрузка от собственной массы плиты (см. табл. 1) равна:

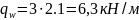, тогда

Напряжение σ_bpна уровне напрягаемой арматуры (т.е. при y_sp=e_0p1), будет равно:

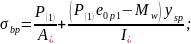
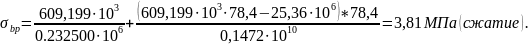
Напряжения σ`_bpна уровне крайнего сжатого волокна при эксплуатации со­ответственно будут равны:

Потери от ползучести бетона определяем по формуле (9.9)[5], принимая значения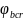 и E_bпо классу бетона равному R_bp= 35 МПа, поскольку принятая передаточная прочность бетона больше 70% класса бетона В35,т.е. R_bp=25MПа>0,7*35=24,5МПа. По таблицам I.3 и I.4 приложения I находим

E_b=34500 МПа, φ_bcr= 2,1(при влажности 50%).

Тогда потери от ползучести соответственно будут равны:

• на уровне растянутой напрягаемой арматуры

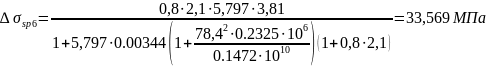
Где a=E_sp/ E_b=200000/34500 = 5.797

=A_sp/A=785/227900=0.00344

С учетом тепловой обработки бетона при атмосферном давлении (по заданию) необходимо умножить полученный результат на коэффициент 0,85. Тогда окончательно получим

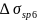=33.569*0,85=28.53Мпа.

• на уровне крайнего сжатого волокна потери напряжений от ползучести при отсутствии арматуры в сжатой при эксплуатации зоне бетона составят:

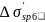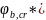=0,8* a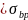 =0,8*2,1*5,797*0,92=8,959МПа.

С учетом тепловой обработки получим

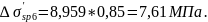
Полные значения первых и вторых потерь предваритель­ного напряжения арматуры составляют:

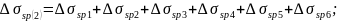
С учетом всех потерь напряжения в напрягаемой арматуре будут равны:

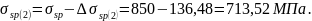
Усилие обжатия с учетом всех потерь определяем по формуле (2.17)[9]

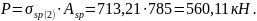
Эксцентриситет усилия обжатия P относительно центра тяжести приве­денного сечения будет равен e_0p= e_0p1= 78,4мм.

Выполним проверку образования трещин в плите для выяснения необхо­димости расчета по ширине раскрытия трещин и выявления случая расчета по деформациям.

Определяем момент образования трещин по формуле (9.36)[5]:

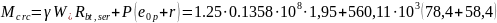
Поскольку M_tot= 107,84 кН·м< M_crc=109,724 кH·м, то трещины в сжатой зоне не образуются ,т.е. не требуется расчет ширины раскрытия трещин.

Определение прогиба плиты в середине пролета от действия постоянных и длительных нагрузок выполняем в соответствии с требованиями пп.4.16-4.20 и 4.24[9].

Для нахождения кривизны определим значения модулей деформации сжатого бетона и коэффициентов приведения арматуры к бетону:

• При непродолжительном действии нагрузок.

E_b1=0,85E_b=0,85*34500=29325 МПа; α=Es/Eb1=200000/29325 = 6,82;

• При продолжительном действии нагрузок.

E_{b1,l=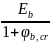 =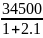} =11129 МПа; α= Es/Eb1,l=200000/11129=17,97.

Определяем характеристики приведенного сечения:

• При непродолжительном действии нагрузки:

A_red=A+ αA_sp=486*143.1+2*38.45*2060+6.22*785=233314.3мм²=0.233314*10⁶ мм²

S_red=S+ αA_spa_p=486*143.1*(220/2)+2060*38.45*(220-38.45/2)+ +2060*38.45*(38.45/2)+6.82*785*30=0.2523*10⁸мм³

y= S_red / A_red=0.2523*10⁸/0.233314*10⁶=108.14мм

I_red=I+ αA_sp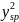 =486*143.1³/10+ 486*143.1*(110-108.4)²+ 2060*38.45³/10+ 2060*38.45*(220-108.14-38.45/2)²+ 2060*38.45³/10+2060*38.45*(108.14-38.45/2)²+ 6.82*785*(108.14-30)² = =0.1504*10¹⁰мм⁴

• При продолжительном действии нагрузки:

A_red=A+ αA_sp=486*143,1+2*2060*38,45+17,97*785=0,242*10⁶мм²

S_red=S+ αA_spa_p=0,2549*10⁸мм³

y= S_red / A_red=0,2549*10⁸/0,242*10⁶=105,3мм

I_red=I+ αA_sp =486*143,1³/10+486*143,1*(110-105,3)² + 2060*38,45³/10+ 2060*38,45* (220-105,3-38,45/2)² +2060*38,45³/10+ 2060*38,45*(107,4-38,45/2)² +17,97*785*(105,3-30)² =0,1556*10¹⁰ мм⁴

Находим кривизну балки при продолжительном действии постоянной и длительной нагрузок по формуле (4.32)[9]:

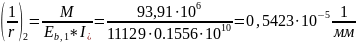
Кривизны от усилия предварительного обжатия Р будут равны:

• От непродолжительного действия усилия предварительного обжатия

• От продолжительного действия усилия предварительного обжатия

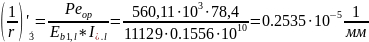
Кривизна, обусловленная выгибом балки вследствие усадки и ползучести бетона от усилия предварительного обжатия составляет:

Где σ_sb = Δσ_sp5+ Δσ_sp6 = 34+28.53=62.53

И σ_sb’ = Δσ΄_sp5+ Δσ΄_sp6 = 34+7.61=41.61

Находим:

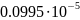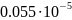= + =0,1545 .

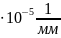Поскольку менее кривизны от усилия предварительного обжатия при продолжительном его действии, то принимаем =0,2535*10^-5. Тогда полная кривизна от действия постоянных и длительных нагрузок будет равна:

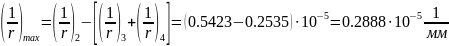
Прогиб балки определяем по формуле (4.25)[9] принимая согласно таблице

IV.8 приложения IV значение S= 5/48 :

f=9.68<f_ult=29.39мм