1. Расчет полки на местный изгиб Расчетный пролет равен

Нагрузка на 1м² полки толщиной 31мм

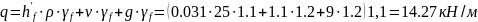
Изгибающий момент для полосы шириной 1м определяем с учетом заделки полки плиты в ребрах по формуле:

Размещаем арматурную сетку в середине сечения полки, тогда 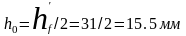. Назначаем диаметр рабочей арматуры сетки 3 мм класса В500 (R_s=435 МПа α_r=0.372).

Тогда, при

< ,

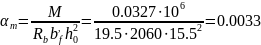Требуемая площадь продольной рабочей арматуры сетки на ширине 1м будет равна:

Принимаем сетку с поперечной рабочей арматурой Ø3 В500 с шагом s=200 мм.

(Ø3 В500 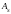=7,1мм²)

2. Проверка прочности плиты по сечениям, наклонным к продоль­ной оси

Поперечная сила на опоре Qmax= 89,26 кН, сплошная равномерно распределенная нагрузка q1 = q = 31,46 кН/м, геометрические размеры расчетного сечения даны на рисунке 1, б.

Поскольку п. 5.12 [9] допускает не устанавливать поперечную арматуру в многопустотных плитах, то выполним сначала проверку прочности наклонных сечений плиты на действие поперечной силы при отсутствии поперечной арматуры согласно п. 3.40 [9].

Проверяем условие (3.70) [9]. Так как 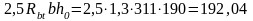кн> кН,

условие выполняется.

Проверяем условие (3.71) [9].принимая приближенно значение Q_b=Q_b,min , а величину проекции опасного наклонного сечения с = h₀ (минимальное значение).

Определение усилия обжатия от растянутой арматуры

кН.

(коэффициент 0,7 учитывает, что потери предварительного напряжения приблизительно будут равны 0,3 ).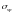

Определение площади бетонного сечения плиты без учета свесов сжатой полки

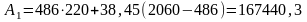мм²

соответственно получим:

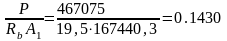, тогда

Находим Q_b,min= 0,5φn Rbt bh₀ = 0,5·1.205·1.3·311·190 =46282 Н=46,28кН.

Поскольку Q=Q_max – q₁c =89,26–31,46·0,19= 83,28 кН>Q_b,min=46.28 кН, то для прочности наклонных сечений плиты требуется поперечная арматура. Так как условие Q< Q_b,min не выполняется.

Устанавливаем в каждом ребре плиты плоский каркас с поперечными стержнями из арматуры класса В500, диаметром 3 мм (A_sw=6*7.1=42.4мм², R_sw = 300МПа), с шагом s_w=90мм<h₀/2=190/2=95мм.

Прочность бетонной полосы проверяем из условия (3.49)[9].

0,3R_bbh₀=0.3*19.5*311*190=345676 H=345.6kH> Q_max =89.26 kH. т.е. прочность бетонной полосы обеспечена.

Прочность по наклонным сечениям проверяем по условию (3.50)[9].

По формуле (3.55)[9] определим усилие в поперечных стержнях на единицу длины элемента

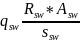= =141.33H/мм.

Проверим условие (3.56)[9]:

0,25φn Rbt b= 0,25*1,205*1,3*311=121,79<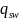 =141.33 H/мм,

т.е. условие выполняется, и Мb будем находить по формуле (3.52) [9]:

Мb=1,5φn Rbt b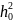 =1.5*1.205*1.3*311*190²=26.38*10⁶H/мм.

Определяем длину проекции невыгоднейшего наклонного сечения с и проекцию наклонной трещины с₀ согласно п.3.33[9].

Так как 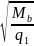= =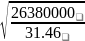916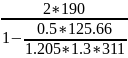мм> = =436.26, то с= =916мм, но так как 3h₀=3*190=570мм<с, принимаем с=3h₀=570мм. Поскольку с₀=с=570 >2h₀=2*190=380, принимаем с₀ =380мм.

Тогда Q_b= Мb/с=26380000/570=46280,7Н=46,28кН=46.28= Q_b,min.

Проверяем условие (3.50)[9], принимая Q в конце наклонного сечения, т.е. Q=Q_max – q₁c =89,26–31,46·0,57=71,32кН.

Q_b +0.75 с₀=46.28+0.75*141.33*0.38=86.55>Q=71.32kH. т.е. прочность наклонного сечения обеспечена.

Согласно п.3.36[9] определим s_w,max по формуле (3.67) [9]

s_w,max =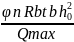 = =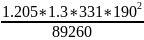197.03>s_w=90мм,

т.е. требования и п.3.36[9] удовлетворены.

Рис 1. Поперечное сечение плиты с овальными пустотами - основные размеры;