2. Случай половинного промежутка.

Допустим, произвольная функция задана на промежутке . Для того, чтобы разложить эту функцию в ряд Фурье, ее необходимо достроить ее произвольным способом на этом же промежутке. Существует 2 способа построения.

1. построение симметрично оси ОУ.

Получим .

будет четной на промежутке , тогда к этой функции можно применить разложение вида:

2. построение симметрично оси ОХ.

Получим .

будет нечетной на промежутке , тогда к этой функции можно применить разложение вида:

3. Случай произвольного промежутка.

, где l – произвольное число. Разложим в ряд Фурье данную функцию. Введем следующую замену:

Тогда разложение будет иметь вид:

, где

Произведя обратную замену и учитывая, что

Тогда:

4. Случай произвольного половинного промежутка

Допустим задана на промежутке . Вводи замену:

если t=0, то m=0

если t=l, то m=π.

Тогда справедливо выражение:

Произведя обратную замену :

Комплексная форма ряда Фурье.

Рассмотрим функцию .

Разложим синус и косинус по формуле Эйлера.

Раскрывая скобки и собирая коэффициенты при и получаем:

- комплексная форма ряда Фурье.

- комплексные коэффициенты разложения периодической функции в ряд Фурье.

- комплексная гармоника.

Определим :

, где

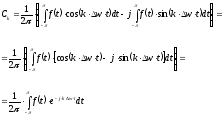
Частный случай интеграла Фурье.

Рассмотри частный случай разложения интеграла Фурье.

- четная:

Если 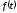- четная, то интеграл Фурье примет вид:

.

- нечетная:

Если - нечетная, то интеграл Фурье примет вид:

.

Комплексная форма интеграла Фурье.

Допустим [11] имеет смысл.

Полученное выражение подставим в [11].

Выражения в круглых скобках в 1 и во 2 слагаемом являются соответственно четной и нечетной функцией относительно w, поэтому.

Сравнивая [13] с выражением для интеграла Фурье [7], приходим к выводу, что они идентичны. Следовательно [11] является комплексной формой интеграла Фурье. В [11] множитель не зависит от следовательно можно его вынести из под знака интеграла. Тогда получим:

Перейдем от к .

Формула 15 имеет своим аналогом комплексную форму ряда Фурье, и здесь роль коэффициента играет внутренний интеграл Обозначим его как:

Тогда [15] примет вид:

Функция 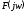является спектральной плотностью функции .

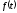Свойства непрерывного спектра. (Свойства преобразований Фурье).

- преобразование Фурье.

- обратное преобразование Фурье.

- свойство линейности.

Линейной комбинации функций соответствует комбинация спектральных характеристик этих функций. Обратное преобразование Фурье от линейных комбинаций спектральных функций имеет вид:

- свойство дифференцирования.

Спектр производной функции определяется как спектр исходной функции умноженной на

.

-свойство интегрирования.

Спектр от интеграла некоторой функции на интервале определяется как спектр исходной функции, деленной на :

-спектр смещенной функции.

Спектр смещенной функции равен спектру исходной функции умноженной на , где - смещение функции.

-изменение масштаба.

(Сжатие или растяжение). Рассмотрим функцию . Построим график функции:

если

В этом случае:

Сжатие исходного сигнала на величину по времени t приводит к расширению спектра в раз по частоте.

-распределение энергии по гармоникам непериодического сигнала:

Найдем спектр от произведения 2 функции:

Если заданы 2 функции , спектры которых соответственно равны:

то спектр от произведения этих функций будет равен:

в случае если , то спектр равен:

Где - энергетическая спектральная характеристика.

-интеграл свертки.

Рассмотрим и на интервале . Функция:

называется сверткой функции и обозначается:

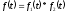
Спектр от свертки функций определяется как произведение спектральных характеристик этих функций:

-спектр от произведения двух функций