
- •3.Числовые характеристики
- •4.Ортогональные и Ортонормальные функции
- •5,6 Тема. Разложение периодической функции в ряд Фурье и частный случай Фурье.
- •Определение коэффициентов ряда Фурье.
- •Частный случай ряда Фурье.
- •Нахождение коэффициентов ряда Фурье от произвольной функции с симметричными пределами.
- •Частные случаи ряда Фурье.
- •Непериодическая функция.
- •Случай половинного промежутка.
- •Случай произвольного промежутка.
- •4. Случай произвольного половинного промежутка
- •Комплексная форма ряда Фурье.
- •Частный случай интеграла Фурье.
- •Комплексная форма интеграла Фурье.
- •Свойства непрерывного спектра. (Свойства преобразований Фурье).
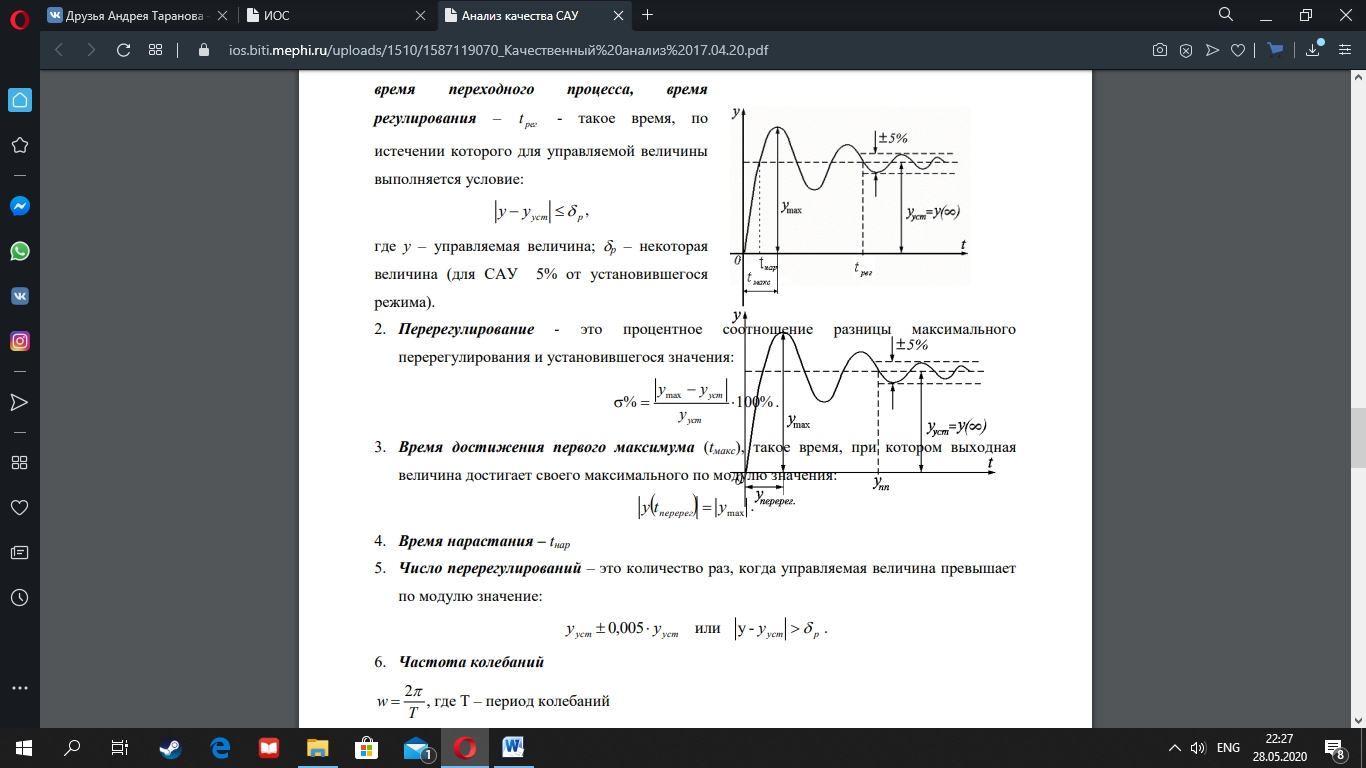
1-Качественный анализ САУ Анализ устойчивости. Система называется устойчивой, если при подаче на ее вход любого возмущающего воздействия, она через некоторый промежуток времени возвращается в устойчивое состояние. При исследовании качества САУ необходимо первоначально исследовать ее устойчивость. Для определения устойчивости системы используют различные алгебраические, частотные и другие методы и критерии. Простейшим при исследовании систем автоматического управления является критерий устойчивости Ляпунова, где устойчивость оценивается по корням характеристического уравнения САУ. Для анализа качества управления могут быть использованы прямые и косвенные методы оценки. Прямые методы определения качества базируются на исследовании переходного процесса, дают наиболее достоверную информацию с последующим определением показаний качества. Косвенные методы определения качества позволяют по косвенным признакам, не решая ни дифференциальных, ни характеристических уравнений, получить приближенный переходный процесс с приближенными показателями качества.
Основные
(прямые) показатели качества САУ
Качество
САУ определяется следующими показателями:
1-
Время достижения установившегося
режима, время переходного процесса,
время регулирования –tрег - такое время,
по истечении которого для управляемой
величины выполняется условие yуст
y
p
, где у – управляемая величина; р
– некоторая величина (для САУ 5% от
установившегося режима).
2-Перерегулирование
- это процентное соотношение разницы
максимального перерегулирования и
установившегося значения:
3-Время достижения первого максимума (tмакс), такое время, при котором выходная величина достигает своего максимального по модулю значения:
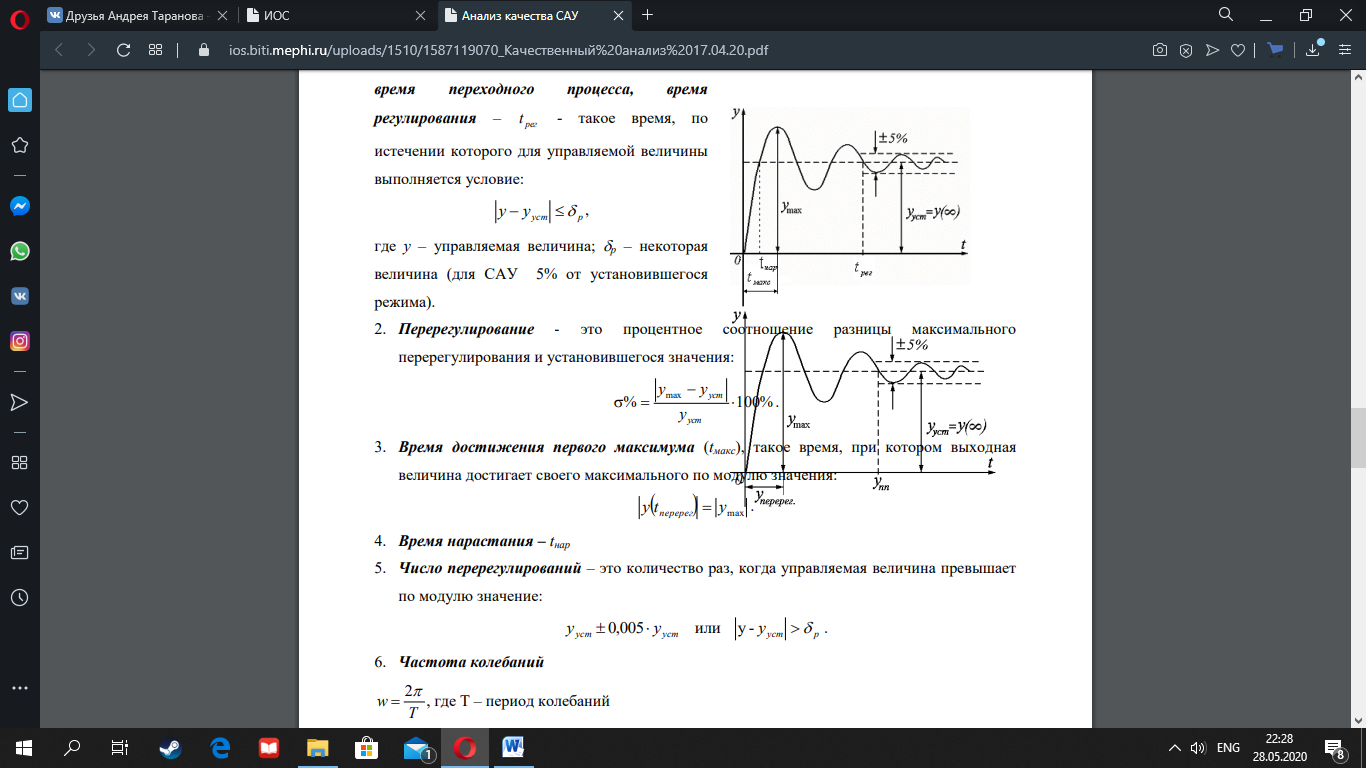 4.
Время нарастания – tнар
5. Число
перерегулирований – это количество
раз, когда управляемая величина превышает
по модулю значение:
4.
Время нарастания – tнар
5. Число
перерегулирований – это количество
раз, когда управляемая величина превышает
по модулю значение:
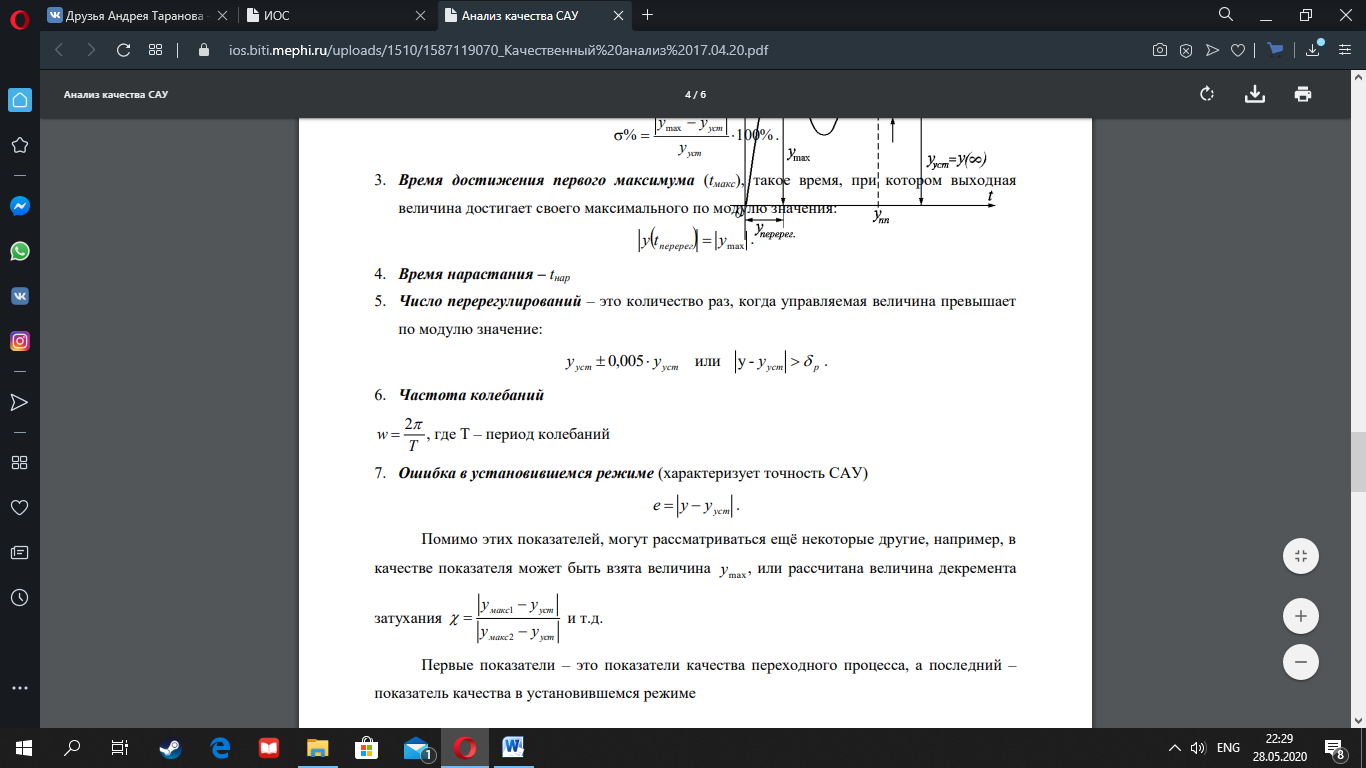 7.
Ошибка в установившемся режиме
(характеризует точность САУ)
7.
Ошибка в установившемся режиме
(характеризует точность САУ)
 Прямые
методы оценки качества (методы построения
переходной характеристики)
1. Решение
дифференциального уравнения (численными
или операторным методами, построение
h(t) по полученным в результате решения
значениям).
2. Частотный метод (позволяет
по виду частотной характеристики P(w)
получить h(t);
3. Моделирование на ЭВМ.
Косвенные
оценки качества
Прямые
методы оценки качества (методы построения
переходной характеристики)
1. Решение
дифференциального уравнения (численными
или операторным методами, построение
h(t) по полученным в результате решения
значениям).
2. Частотный метод (позволяет
по виду частотной характеристики P(w)
получить h(t);
3. Моделирование на ЭВМ.
Косвенные
оценки качества
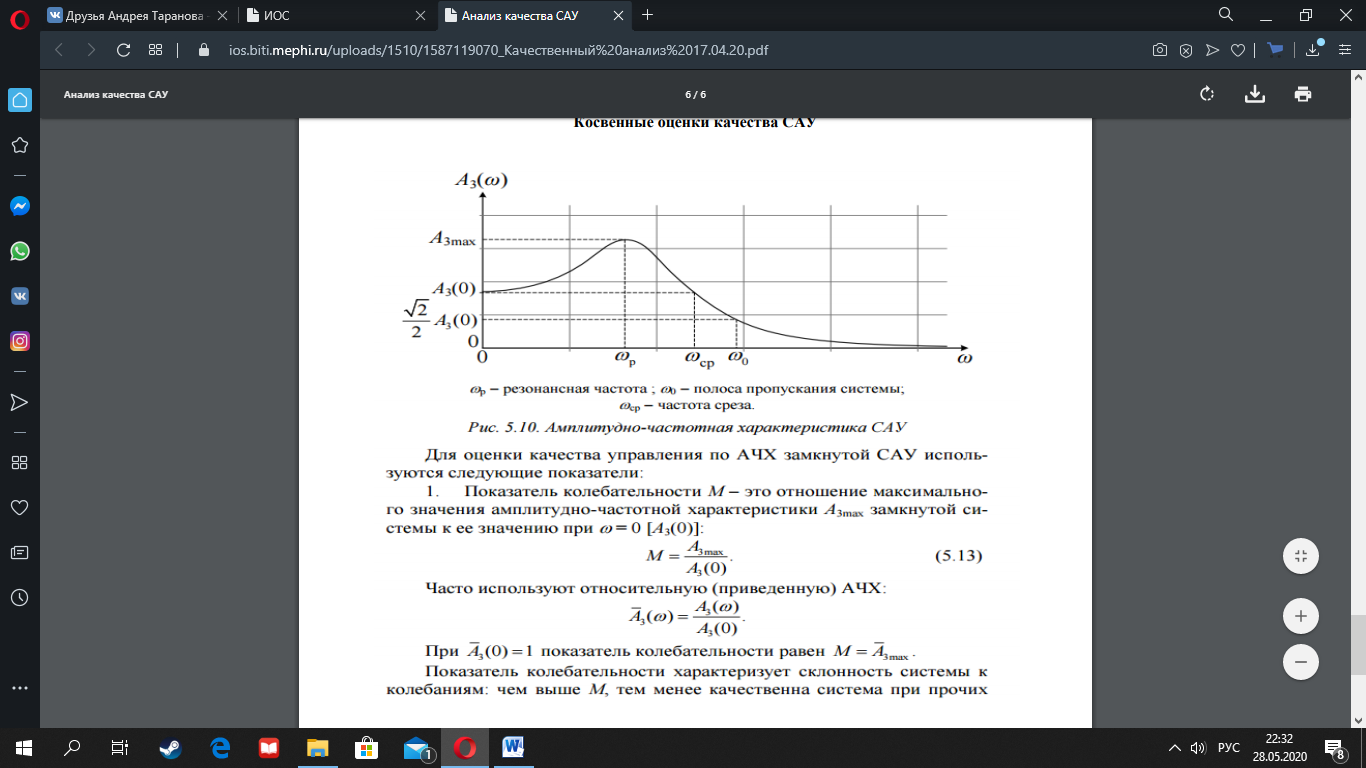
1.Резонансная
частота
– определяется как частота, в которой
АЧХ достигает своего максимального
значения wр.
2.
Показатель колебательности
– определяется как отношение амплитуд:
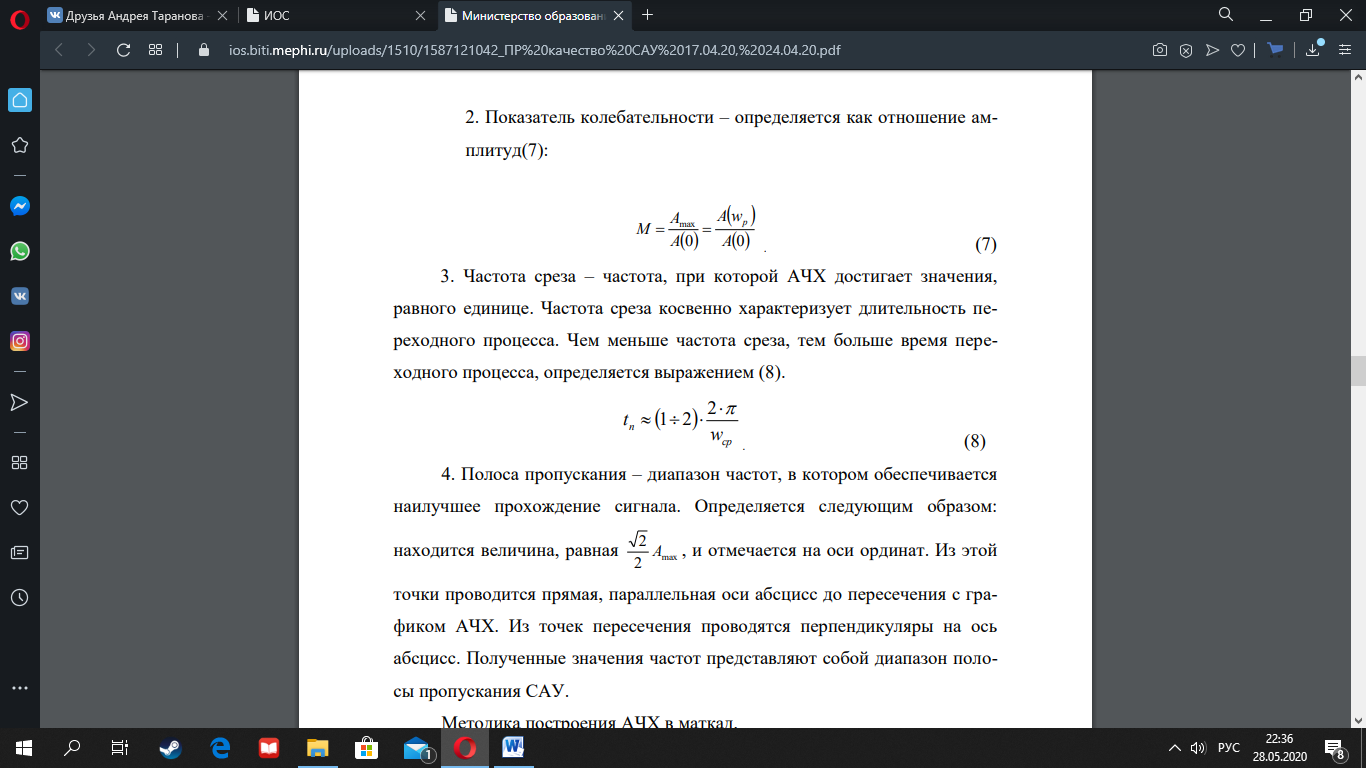 3.
Частота среза
– частота, при которой АЧХ достигает
значения, равного единице. Частота среза
косвенно характеризует длительность
переходного процесса. Чем меньше частота
среза, тем больше время переходного
процесса, определяется выражением
3.
Частота среза
– частота, при которой АЧХ достигает
значения, равного единице. Частота среза
косвенно характеризует длительность
переходного процесса. Чем меньше частота
среза, тем больше время переходного
процесса, определяется выражением
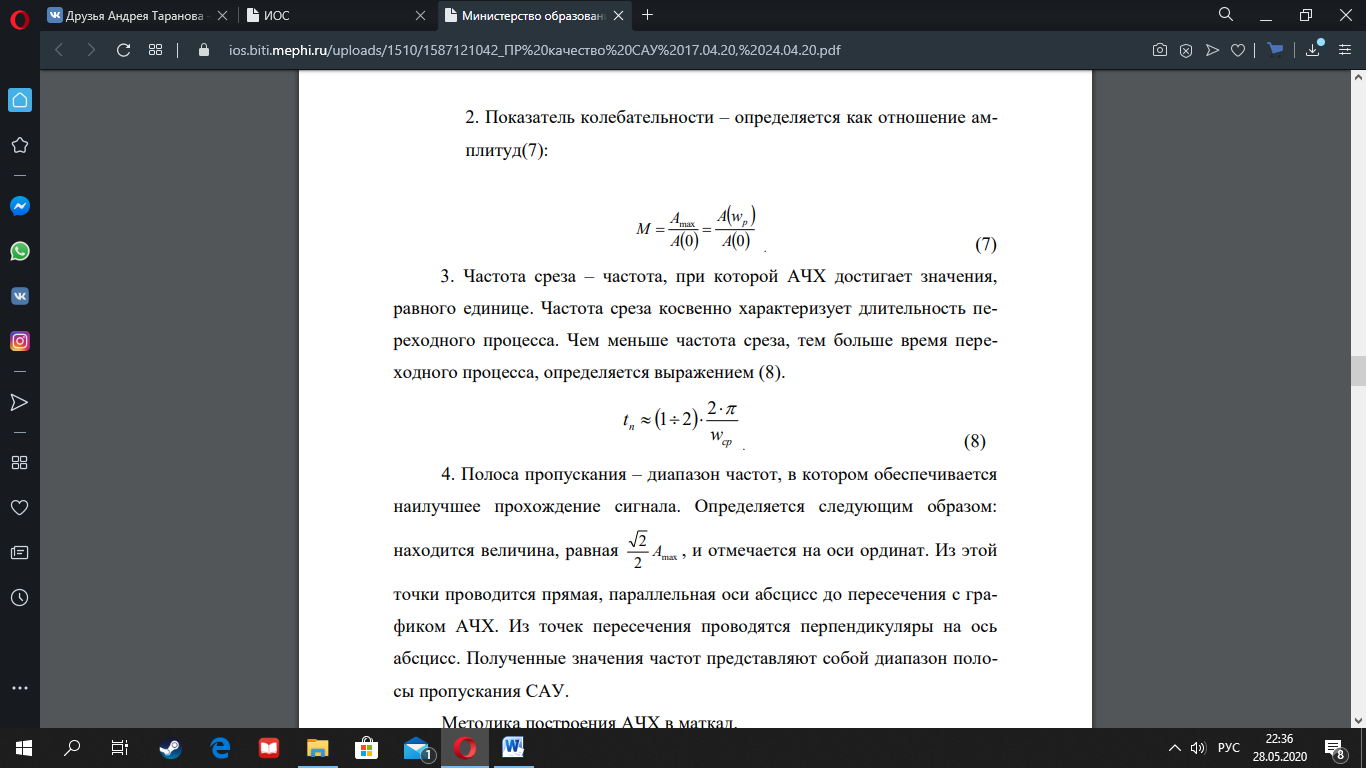 4.
Полоса пропускания
– диапазон частот, в котором обеспечивается
4.
Полоса пропускания
– диапазон частот, в котором обеспечивается
наилучшее прохождение сигнала. Определяется следующим образом:
находится
величина, равная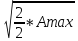 , и отмечается на оси ординат. Из этой
точки проводится прямая, параллельная
оси абсцисс до пересечения с графиком
АЧХ. Из точек пересечения проводятся
перпендикуляры на осьабсцисс. Полученные
значения частот представляют собой
диапазон полосы пропускания САУ.
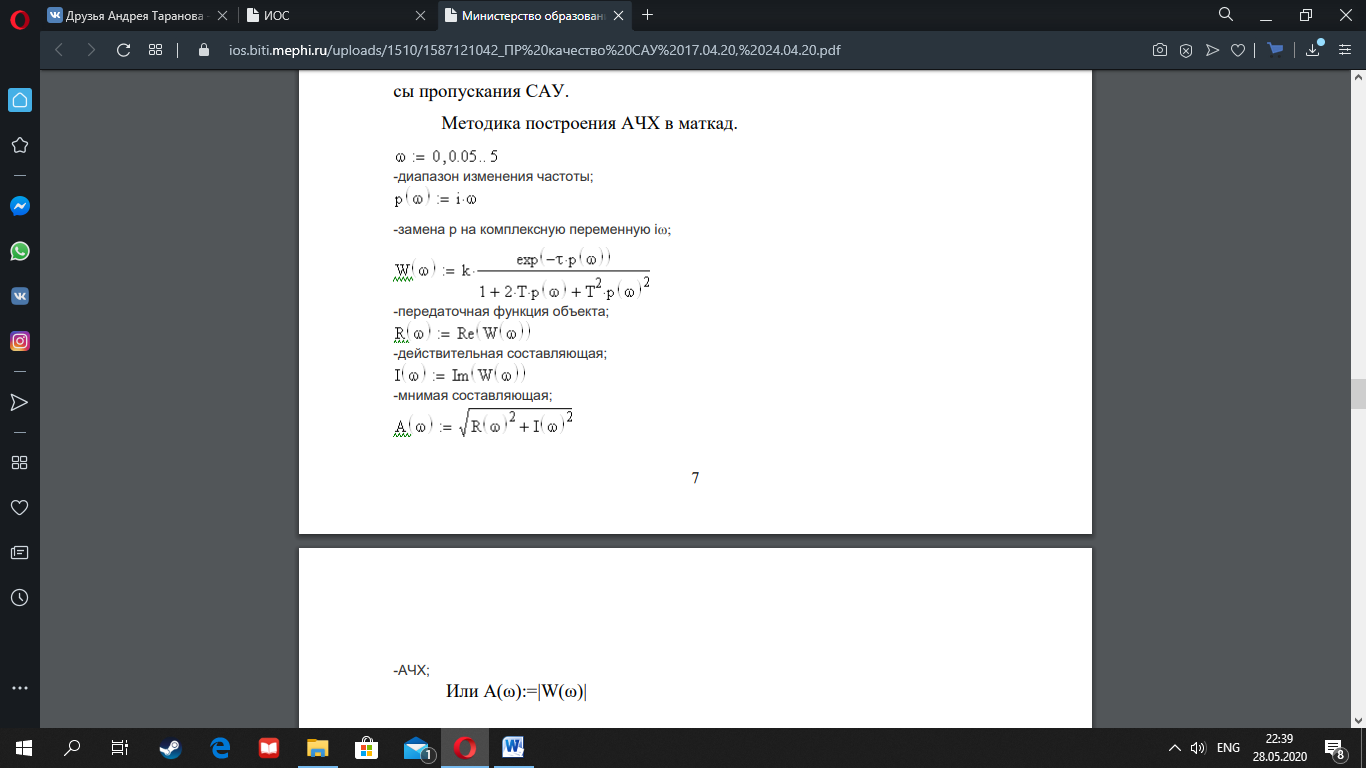
Методика
построения АЧХ
, и отмечается на оси ординат. Из этой
точки проводится прямая, параллельная
оси абсцисс до пересечения с графиком
АЧХ. Из точек пересечения проводятся
перпендикуляры на осьабсцисс. Полученные
значения частот представляют собой
диапазон полосы пропускания САУ.
Методика
построения АЧХ
2-ТЕОРИЯ
АВТОМАТОВ
Графическое
задание автоматов
Граф
конечного автомата строится таким
образом, что его вершины соответствуют
состояниям, а дуги, направленные из i-й
вершины в j-ю, обозначаются дизъюнкциями
дробей вход-выход (либо дизъюнкцией пар
входвыход). Под входом понимается входной
сигнал, под воздействием которого
осуществляется переход из состояния i
в состояние j. Выход – сигнал на выходе
автомата при этом переходе.
 Теория
автоматов
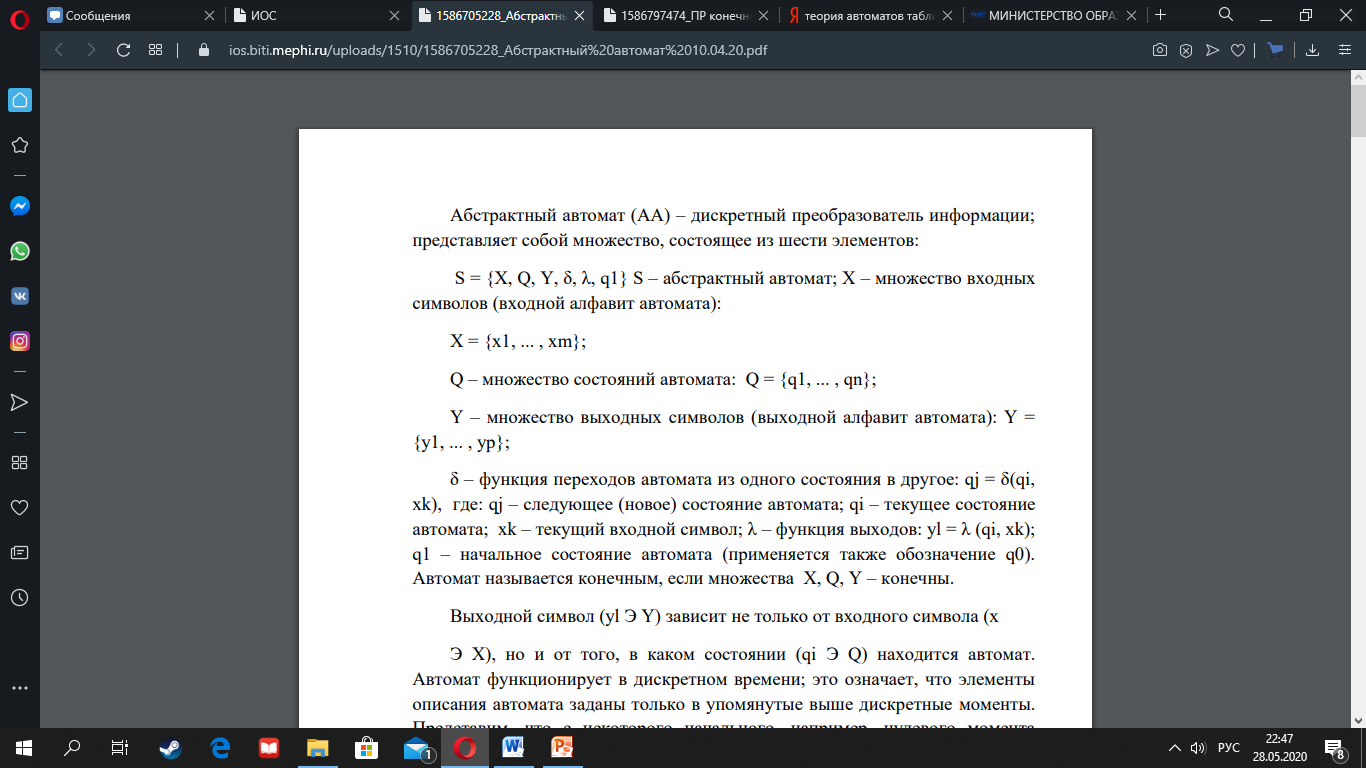
Абстрактный
автомат (АА) – дискретный преобразователь
информации; представляет собой множество,
состоящее из шести элементов:
Теория
автоматов
Абстрактный
автомат (АА) – дискретный преобразователь
информации; представляет собой множество,
состоящее из шести элементов:


Аналитическое способ задания автомата

Табличный
способ задания автомата
 Конечным
автоматом
называется техническое устройство,
имеющее несколько входов, несколько
выходов и несколько внутренних состояний,
которое предназначено для преобразования
дискретной информации.
Функции
выходов и переходов называются
характеристическими функциями.
Конечным
автоматом
называется техническое устройство,
имеющее несколько входов, несколько
выходов и несколько внутренних состояний,
которое предназначено для преобразования
дискретной информации.
Функции
выходов и переходов называются
характеристическими функциями.
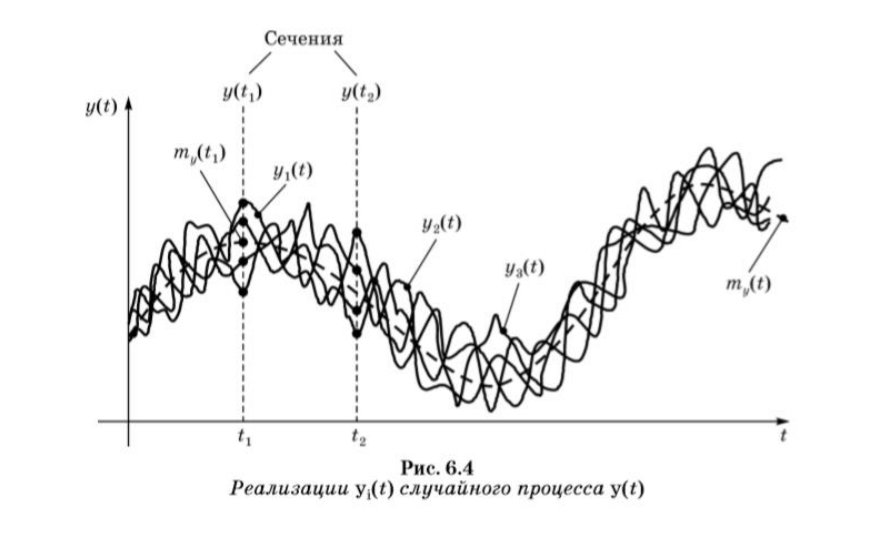
3.Числовые характеристики
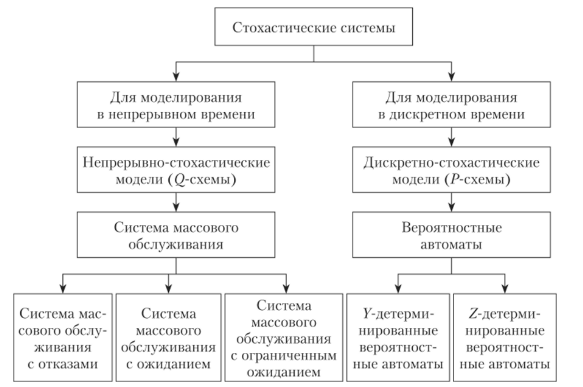
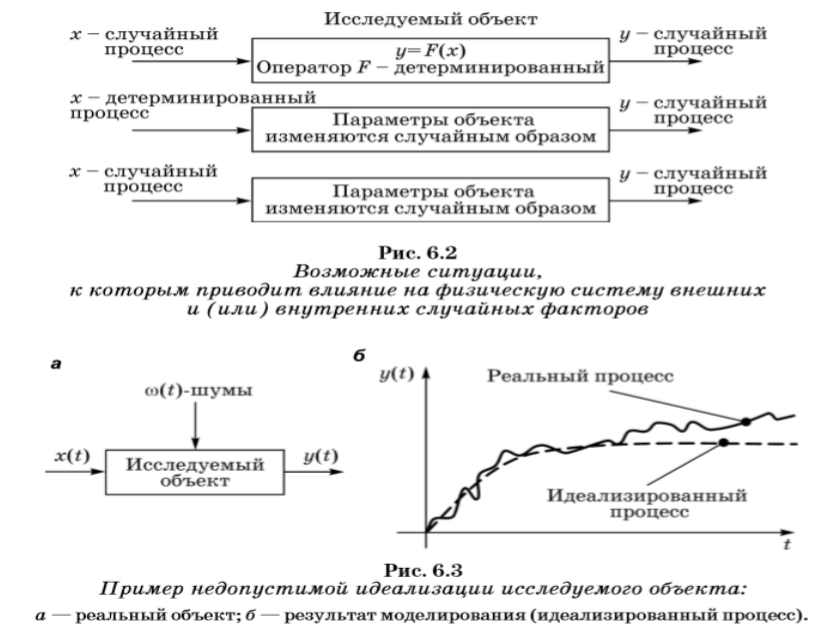
Стохастические системы — это системы, изменения в которых происходят под воздействием случайных факторов. Для их описания вводится случайный оператор со, описывающий пространство элементарных событий с вероятностной мерой и учитывающий, как случайные начальные состояния системы, так и случайные переходы, и выходы.
которые наиболее часто используются для моделирования стохастических систем.


4.Ортогональные и Ортонормальные функции


5,6 Тема. Разложение периодической функции в ряд Фурье и частный случай Фурье.
Функция
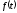 называется периодической с некоторым
периодом T>0, если значение функции в
точке
называется периодической с некоторым
периодом T>0, если значение функции в
точке
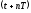 равно значению функции в точке t:
равно значению функции в точке t:
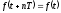
Для периодической функции выполняется следующее равенство:
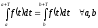
Рассмотрим гармонический процесс вида:
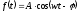
рисунок 1
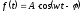 ,
где
,
где
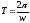
Рассмотрим функции:
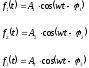
Сумма этих функций приводит к образованию некоторой новой функции с периодом Т.
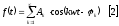 .
.
Теорема.
Функция
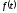 ,
представляющая собой сумму бесконечного
ряда, является периодической и ее период
совпадает с периодом Т первой гармоники.
Частоты соседних гармоник отличаются
на величину
,
представляющая собой сумму бесконечного
ряда, является периодической и ее период
совпадает с периодом Т первой гармоники.
Частоты соседних гармоник отличаются
на величину
 .
.
Доказательство.
Обозначим
приращение частоты при переходе от
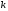 к
к
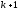 гармоники через
гармоники через
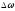 ,
тогда для [2] получим:
,
тогда для [2] получим:
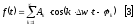 .
.
Общий
член ряда [3]
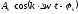 называется
называется
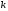 -ой
гармоникой ряда. Частота
-ой
гармоникой ряда. Частота
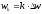 - называется частотой
- называется частотой
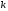 -ой
гармоники.
-ой
гармоники.
Представим некоторую функцию в виде суммы гармонических функций и предположим, что существует нулевая гармоника А0.
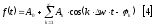
Распишем косинус разности:
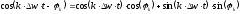
Тогда
для
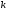 -ой
гармоники:
-ой
гармоники:
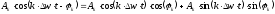
Обозначим:
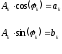
Тогда:
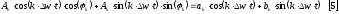
Обозначим:
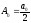
Тогда [4] примет вид:

Это
тригонометрическая форма ряда Фурье.
Если
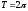 ,
то
,
то
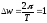 .
В таком случае для периодической функции
с периодом
.
В таком случае для периодической функции
с периодом
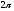 ряд Фурье будет иметь следующий вид:
ряд Фурье будет иметь следующий вид:
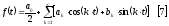
Определение коэффициентов ряда Фурье.
Для
разложения в ряд Фурье периодических
функций с периодом
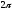 используется ряд ортогональных функций
следующего вида:
используется ряд ортогональных функций
следующего вида:
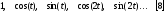 .
.
Проинтегрируем
[7]
на промежутке
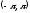 .
.
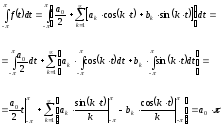
Выразим а0.
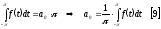
Определим
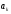 и
и
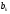 .
Для этого [7] умножим на
.
Для этого [7] умножим на
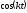 .
В результате получим:
.
В результате получим:
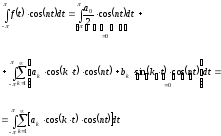
Так
как система функций [8] ортогональна
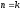 ,
то:
,
то:
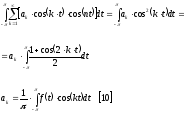
Для
определения коэффициента
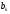 ,
[7] умножим на
,
[7] умножим на
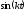 .
В результате получим:
.
В результате получим:
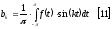
Формулы [9], [10], [11] являются формулами для определения коэффициентов ряда Фурье. Зная их можно найти амплитуду и начальную фазу k-ой гармрмоники:
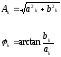
Частный случай ряда Фурье.
Допустим
функция
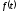 на промежутке
на промежутке
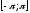 является нечетной, тогда:
является нечетной, тогда:
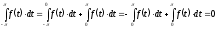
Интеграл от нечетной функции в симметричных пределах равен нулю.
Допустим
функция
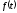 на промежутке
на промежутке
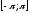 является четной, тогда:
является четной, тогда:

Интеграл от нечетной функции в симметричных пределах равен удвоенному интегралу в пределах, равных половине симметричной области.
Нахождение коэффициентов ряда Фурье от произвольной функции с симметричными пределами.
Допустим
функция
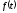 является четной, тогда интеграл имеет
вид:
является четной, тогда интеграл имеет
вид:
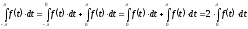
Если:
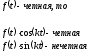
Найдем коэффициенты ряда Фурье:
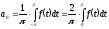
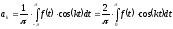
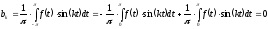
Ряд Фурье для четной функции имеет вид:
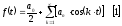
Допустим
функция
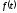 является нечетной, тогда интеграл имеет
вид:
является нечетной, тогда интеграл имеет
вид:
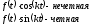
Найдем коэффициенты ряда Фурье для этого случая:
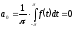
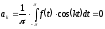
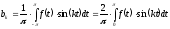
Ряд Фурье для этого случая имеет вид:
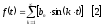
Частные случаи ряда Фурье.
Рассмотрим 4 частных случая ряда Фурье:
-
Непериодическая функция.

Исходную
функцию
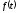 периодически продолжаем вне интервала
периодически продолжаем вне интервала
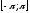 на всю ось, и функция, получившаяся в
этом случае является периодической с
периодом
на всю ось, и функция, получившаяся в
этом случае является периодической с
периодом
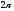 ,
и на интервале
,
и на интервале
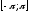 она будет полностью совпадать с исходной
функцией, следовательно, для нее можно
применить разложение в ряд Фурье,
рассмотренное ранее Если функция четная,
то разложение [1], если нечетная – [2]..
она будет полностью совпадать с исходной
функцией, следовательно, для нее можно
применить разложение в ряд Фурье,
рассмотренное ранее Если функция четная,
то разложение [1], если нечетная – [2]..
