2 семестр / практика 8-9 1 вариант / 8-9

Практическая работа №8 РАЗЛОЖЕНИЕ ФУНКЦИИ В РЯД ФУРЬЕ

ЦЕЛЬ РАБОТЫ: приобрести навыки разложения функции в ряд Фурье и определения коэффициентов ряда на различных промежутках.

Задание: Вычислить первые четыре пары коэффициентов разложения в ряд Фурье функции f(t) на отрезке [0, 2 ]. Построить графики 1, 2 и n гармоник. n – число гармоник для вариантов 1-5 имеет значение n=4. Выполнить гармонический синтез функции f(t) по 1, 2 и n гармоникам. Результаты синтеза отобразить графически.

Функция 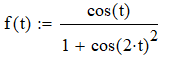является четной. Следовательно, решение будет иметь следующий вид:

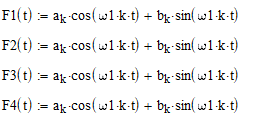
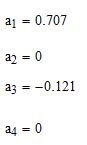
Постоим график 4 гармоник и гармонический синтез функции с учетом того что заданная функция f(t) - четная.

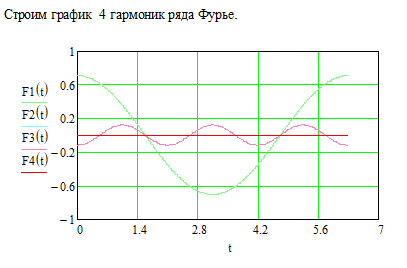
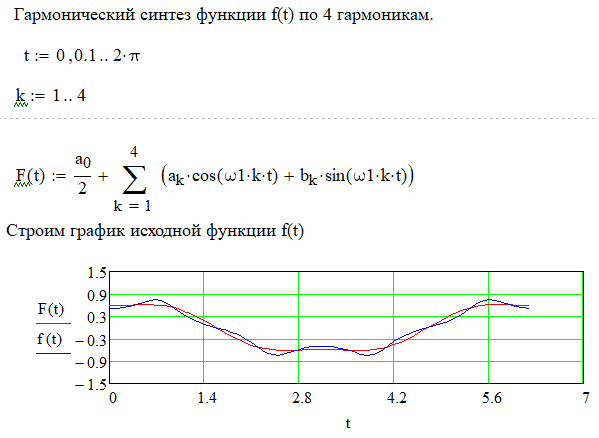
Данные работы номер 8 используются в работе 9.

Практическая работа №9 СПЕКТРЫ НЕПРЕРЫВНЫХ ФУНКЦИЙ

ЦЕЛЬ РАБОТЫ: приобрести навыки спектрального анализа непрерывной периодической функции, построения графиков частотных спектров функции и графиков амплитудно- и фазочастотных спектров.

Задание: Провести спектральный анализ непрерывной периодической функции, заданной на интервале от 0 до 2π. И построить графики частотных спектров функции и графики амплитудно- и фазочастотных спектров. Для выполнения задания необходимо взять функцию из работы №8 и провести построение графика частотного спектра, по рассчитанным значениям коэффициентов р. Фурье. Рассчитать амплитудно- частотные и фазо-частотные спектры по выражениям:

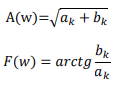
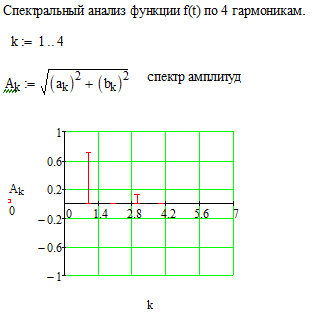
Построим 4 спектров так как в задании практики 8 нужно было составить 4 пар коэфициентов

Так как 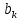=0, то фазочастный спектр будет равен 0

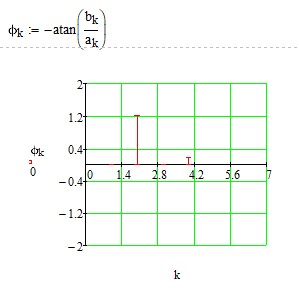
Вывод: приобрел навыки разложения функции в ряд Фурье

и научился находить коэффициенты ряда на различных промежутках.