Критерий Романовского.

Если в ряде измерений х1,х2,...,хk,xn результат измерения хк является грубым, то следует найти среднее арифметическое значение x и среднее квадратическое значение   для группы (n-1) ряда измерений. Затем обозначим    где  2  x дисперсия разности   равна сумме дисперсий случайных величин xk и   Тогда   , (1.18) где   - дисперсия среднего арифметического ряда измерений. Величина t будет подчинена распределению Стьюдента с параметром k=n-1. Это позволяет найти вероятность случайного распределения  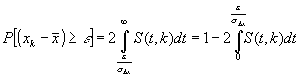 где S(t,k) - гамма-функция. Для упрощения практических расчётов можно использовать значения величин   приведены в таблице 1.1 для вероятности   случайного расхождения   Пользуясь этой таблицей, можно найти такие значения t'  , для которых   т. е. задаваясь вероятностью   , обеспечивающей практическую необходимость события, можно определить значение интервала   , являющееся критерием грубой погрешности.

20)Критерий вариационного размаха

22)Критерий «3 σ»

Критерий "трех сигм" применяется для результатов измерений, распределенных по нормальному закону. По этому критерию считается, что результат, возникающий с вероятностью q < 0,003, маловероятен и его можно считать промахом, если |х̅-х_i| > 3S_x , где S_x — оценка СКО измерений. Величины х и S_x вычисляют без учета экстремальных значений x_i. Данный критерий надежен при числе измерений n > 20... 50.

21)Критерий Диксона

     Критерий Диксона основан на предположении, что результаты измерений подчиняются нормальному закону распределения. При его использовании полученные результаты единичных измерений записывают в вариационный возрастающий ряд.

 Критерий Диксона определяется как

Если К_Д  больше критического значения  Z_q  (см. таблицу 2) при заданном уровне значимости q (q = 1 - P), то результат  x_j  считают промахом.

23)Критерий Шовене используется для оценки на грубую погрешность одного сомнительного значения выборки из нормально распределённой случайной величины . Иногда указывают, что критерий Шовене применим для выборок объёмом n не боьше 10 [1] или 20 [2].

Алгоритм критерия Шовене, описанный в [3], можно интерпретировать так:

1). Находят модуль приведённого сомнительного значения t:

t = |х_с - х_ср|/s                 (1)

Здесь х_с - сомнительное значение (наибольшее или наименьшее в выборке), х_ср - среднее значение выборки, s - выборочное среднеквадратическое отклонение

2). Определяют значение интегральной функции стандартного нормального распределения F(t).

3). Рассчитывают вероятность Р_прев получения результата, который по модулю превышает модуль х_с:

Р_прев = (1 – F(t))•2                (2)

4). Находят ожидаемое число результатов N, отклоняющихся при данном объёме выборки n от среднего значения больше, чем х_с :

N = Р_прев•n                (3)

Если N < 0,5, сомнительное значение считают грубой ошибкой. В зависимости от решаемой измерительной задачи экспериментатор может, как указано в [3], использовать иное значение N.

В литературе встречаются и другие алгоритмы применения критерия Шовене, например, описанные в [1], [2] , которые дают аналогичные результаты.

Преимущество критерия Шовене состоит в том, что нет надобности в таблице критических значений.

Недостатки критерия Шовене:

1). Для критическоих значений N, в частности, для 0,5, в литературе отсутствуют уровни значимости, что снижает информативность критерия.

2). Возможность использовать значение N по выбору экспериментатора без учёта уровня значимости, несомненно, повышает субъективность критерия.

Задачи исследования.

1). Найти уровни значимости для критерия Шовене при критических значениях N в пределах от 0,2 до 0,8 при шаге варьирования 0,1.

2). Найти критические значения N при общепринятых ("стандартных") уровнях значимости.

Результаты исследования.

Выражение (3) с учётом (2) можно представить в виде

1 – F(t) = N/2n                (4)

Выражение (1) для t представляет собой расчётную формулу для критерия Н.В. Смирнова (другое название - критерий Граббса). Следовательно, критерий Шовене сводится к критерию Н.В. Смирнова, но при иных значениях процентных точек. Если подставить в выражение (4) какие-либо значения n и N, можно найти критическое значение t, соответствующее процентной точке критерия Н.В. Смирнова при некотором уровне значимости α, а также выбранному N. Уровень значимости, в принципе, можно найти из таблицы процентных точек критерия Н.В.Смирнова по критическому значению t и объёму выборки n. Однако при округлённых значениях N, равных 0,5 или других, получаются значения t, не соответствующие общепринятым ("стандартным") уровням значимости, и отсутствующие в таблице процентных точек критерия Н.В.Смирнова. Поэтому уровни значимости были рассчитаны методом статистического компьютерного моделированя в MS Excel для максимальных значений выборки. Легко показать, что для минимальных значений выборки уровни значимости будут такими же. Моделировали 10⁶ выборок. Результаты приведены в таблице 1. Прочерки в таблице 1 означают, что уровень значимости меньше 0,000001, т.е. все полученные при моделировании значения N были больше того, по которому определяли уровень значимости.

24 )Критерий Шарлье [1] используется для оценки на грубые погрешности сомнительных значений выборки из нормально распределённой случайной величины . Критерий применяют для выборок, в которых число наблюдений n превышает 20. По критерию Шарлье сомнительное значение х_с считают грубой ошибкой, если выполняется неравенство

|х_с - x_ср| > К_шS,

где x_ср - среднее значение выборки, К_ш - табличное значение критерия Шарлье, S - выборочное среднеквадратическое отклонение.

К недостаткам критерия Шарлье можно отнести отсутствие в литературе уровней значимости для табличных значений. Кроме того, как показано в [2], табличные значения критерия Шарлье выглядят сомнительно. Это подтверждается ещё и тем, что неравенство, определяющее грубую ошибку, можно преобразовать так:

|х_с - x_ср|/S > К_ш

Но это выражение соответствует расчётной формуле для критерия Н.В. Смирнова (иначе говоря, для критерия Граббса). Таким образом, критерий Шарлье сводится к критерию Н.В. Смирнова. Однако, если сравнить табличные значения критерия Н.В. Смирнова (Граббса) и критерия Шарлье, видно, что уровни значимости для табличных значений критерия Шарлье явно выше 0,1.

Уровни значимости α табличных значений критерия Шарлье были рассчитаны методом статистического компьютерного моделирования в MS Excel. Результаты приведены в таблице.

n	3	4	5	6	7	8	9	10	11	12	13	14	15
Кш	0,97	1,15	1,3	1,38	1,47	1,53	1,59	1,65	1,69	1,73	1,77	1,8	1,83
α	0,548	0,467	0,411	0,421	0,403	0,408	0,404	0,392	0,396	0,395	0,391	0,394	0,394
n	16	17	18	19	20	30	40	50	60	70	80	90	100
Кш	1,86	1,89	1,91	1,94	1,96	2,13	2,24	2,32	2,40	2,45	2,50	2,54	2,58
α	0,391	0,388	0,392	0,385	0,387	0,382	0,385	0,390	0,379	0,385	0,383	0,385	0,381

Как видно из таблицы, при любых объёмах выборки вплоть до 100 уровни значимости для табличных значений критерия Шарлье очень велики, что означает высокую вероятность (практически не менее 38%) того, что приемлемое максимальное или минимальное значение выборки будет принято за грубую погрешность. Такие уровни значимости вряд ли приемлемы. Поэтому использование критерия Шарлье следует признать нецелесообразным.