2. Тарау. Кристалдардағы дифракция

Заттың атомдық құрылымының зерттеуі рентген сәулелерінің, электрондардың және нейтрондардың дифракция құбылысына негізделген. Шашырау табиғатының атомдардың кеңістік орналасуымен байланысын зерттейтін дифракция теориясы сәулеленудің үш түрі үшін бірдей болып келеді. Дифракциялық бейне алу үшін қолданылатын сәулеленудің толқын ұзындығы орташа атомаралық қашықтықпен сәйкес болуы қажет. Атомдар арасындағы қашықтық 1-4 Å аралығында. Толқын ұзындығы бірнеше мың ангстремге тең көрнекілік жарық толқындары үшін дифракция бақыланбайды. Толқын ұзындығы ~1 Å рентген сәулелері, нейтрондар және электрондар атомдар жиынтығымен шашыратқанда, интерференциялық эффектілер байқалады. Құрылымның зерттеуінің дифракциялық әдістері есептеулі болып келеді. Кристалдағы толқындар дифракциясы арқылы элементарлы ұяшық өлшемі, ядролар орналасуы және ұяшықтағы электрондар таралуы туралы мәлімет алуға болады. Есептеулер үшін кристалдық тор түймелеріндегі сәулелену шашыраған кездегі интерференциялық максимумдар орналасуын білу қажет.

Кристалдардағы дифракцияны кристалдық тор жазықтықтарынан сәулелердің (рентген сәулеленуін қарастырғанда – рентген сәулелерін) шағылуы ретінде қарастыруға болады (Сурет 6).

Сурет 6. Кристалдардағы дифракция құбылысы

Параллел жазықтықтармен шашыратылған толқындар бір фазада болып, бір бірін күшейткенде, яғни, көршілес жазықтықтардан шашыраған кезде жол айырымы толқын ұзындықтарының бүтін санына тең болса ғана, шағылу байқалады . (3.1)

Бұл формула - тордағы жазықтықтар арасындағы қашықтықты шашыраған шоғырлардың бағытымен ( бұрыштары) байланыстыратын Вульф-Брэгг формуласы; n- шағылу реті. Вульф-Брэгг формуласы бойынша, берілген үшін дифракциялық шоғырларды монохроматты сәулеленуде алуға болады, яғни кристалдың бағытын өзгерту арқылы тұрақты  толқын ұзындығында, ал козғалмайтын кристалл үшін – полихроматты сәулелену кезінде алынады, бұл жағдайда дифракциялық шоғырлар шағылуға сәйкес келетін  толқын ұзындығында пайда болады.

Егер бастапқы толқын түсетін нысан шашырататын қабілеті , нүктелерінде орналасқан және тарататын орталықтар саны болса, онда қорытқы амплитуда: . (3.2)

, , - түсетін толқынның толқындық векторы, - шашыраған толқынның толқындық векторы, – берілген нысанның шашырау амплитудасы. рентген сәулелерінің нысанға түсуі кезінде толқындарды шашырататын «физикалық нүктелер» ретінде электрондар қарастырылады. Олардың әрқайсысы бастапқының толқын ұзындығындай, жиілігіндей екінші рет шашыраған толқынның көзіне айналады. Егер бір электронмен шашыратқан амплитудасын бірге тең деп алсақ, онда шашырау амплитудасы: . (3.3)

Электрондық тығыздық функциясы. күйіндегі n-нүктелерінің дискретті жиынтығы орнына нысанның тең үлестірілген шашыратқыш қабілетін қарастырады. Рентгендік сәулелер электрондармен шашырайтын болғандықтан, олар үшін «шашырататын матрица» ретінде нысанның уақыт бойынша орташа электрондық тығыздығы болып келеді. Бұл функция нүктесінің қасындағы көлем элементіндегі электрондардың орташа санының көлем элементіне қатынасына тең: . (3.4)

Атомдық амплитуда (атомдық фактор). Рентген шағылуларының интенсивтілігі кристалдық тордағы атомның шашыратқыш қабілетіне тура пропорционал. Атомға түсетін жазық монохроматты толқын оның әрбір dV элементінде элементар екінші ретті толқынды қоздырады. Шашыраған толқынның амплитудасы көлемнің берілген элементінің шашыратқыш қабілетіне пропорционал, ал ол өз кезегінде шамасына пропорционал. Атоммен шашырайтын қорытынды толқынның амплитудасының электронмен шашырайтын толқынның амплитудасына қатынасын көрсететін сан бірдей жағдайда (бірдей бұрышта және толқын ұзындығында) атоммен үлестірілуі функциясы бар элементтің шашырауы болып келеді:

(3.5)

Өте кіші шамаларында синустың аргументке қатынасы бірлікке жақын және , –атомдағы электрондар саны (элементтің атомдық номері).

Температуралық фактор. Кристалдағы атомдар жылулық қозғалыс күйінде болады. Шашырауды анықтайтын электронды тығыздық функциясы уақыт бойынша орташа электрондық тығыздық болып келеді. Дифракциялық эксперименттің ұзақтығы атомдардың жылулық тербелісінің периодтарынан анағұрлым артық болып келеді. Жылулық қозғалысты ескеру үшін (r) атом орталықтарының олардың тепе-теңдік күйіне қатысты үлестірілуінің функцияларын білу қажет: , мұнда - атомның тепе теңдік күйінен орташа квадратты ығысуы. Температуралық фактор:

. (3.6)

Лауэ шарты. Лауэ шарттарын құру келесі ойларға негізделген: егер қатты дене кристалдық күйде болса, онда қасиеттері бойынша ұқсас түймелер параллел қатарлармен орналасатын бағыт болады және осындай әр қатарда олар а трансляциясымен байланысқан. Егер осындай қатарға кез келген ₀ бұрышпен толқын ұзындығы  параллел монохроматты сәулеленудің шоғырын бағыттасақ, онда шағылу бір бірімен а трансляциясымен байланысқан түймелердің барлық қосылатын шағылулары бір фазада болатын бағыттарда пайда болады (Сурет 7).

Бұл жағдай екі көршілес түймеден шашыраған толқындардың жол айырымы толқын ұзындықтарының бүтін санына тең болғанда мүмкін:

, (3.7)

мұнда -шағылу бағыты және қатардың бағыты арасындағы бұрыш; h – интерференция индексі (бүтін сан).

Сурет 7. Шағылу бағыттары

Трансляциялары a, b, c үшөлшемді периодикалық торда Лауэ теңдеулері келесі түрде жазылады: 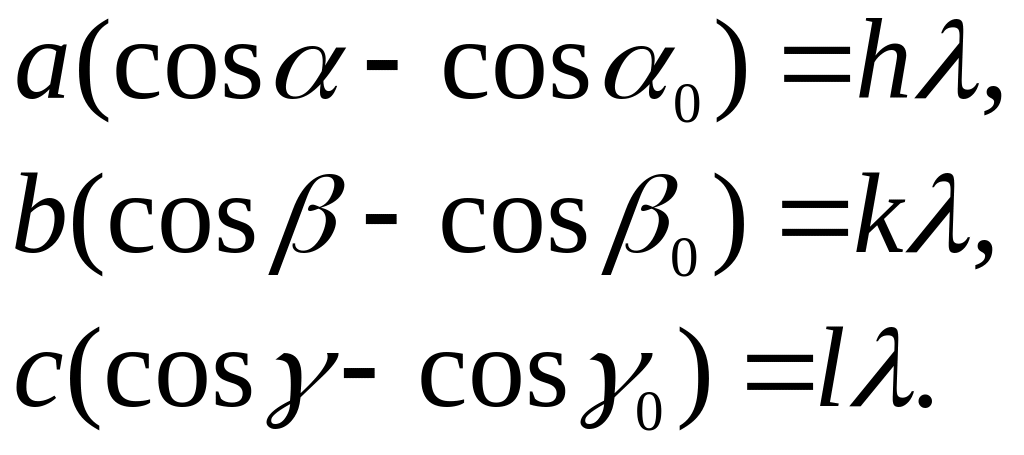(3.8)

Интерференциялық сәулелердің бағытын анықтайтын кеңістіктегі Лауэның үш теңдеуін жалпы түрде кері тор арқылы геометриялық түрде интерференция шартын интерпретация жасайтын бір интерференциялық теңдеумен алмастыруға болады: ;

мұнда және , сәйкесінше, түсетін және шағылатын сәулелердің бағыттаушы косинустары. Бұл теңдеу толықтай интерференциялық сәулелердің орнын анықтап, Лауэ теңдеуін және Вульф-Брэгг теңдеуін біріктіреді. Оны пайдаланып, кері торды және шағылу сферасын (Эвальд сферасын) геометриялық тұрғыдан құрып, интерференциялық сәулелердің бағытын анықтауға болады.

Құрылымдық фактор. Егер екі түрлі заттың элементарлы ұяшықтары пішін бойынша бірдей және өлшемі бойынша сәйкес болған жағдайда, рентгенограммалардағы рефлекстердің геометриялық орны ұяшықта қанша атом болса да, әрқашан бірдей болып келеді. Егер элементарлы ұяшықтар пішін бойынша бірдей болып, бірақ өлшемдері әртүрлі болса, онда сәйкес рентгенограммалардағы геометриялық орны тек масштабтарымен ғана ерекшеленеді. Геометриялық бірдей рефлекстердің айырмашылығы интенсивтіліктерінде ғана байқалады. Рефлекстердің кейбір бөліктерінің интенсивтіліктері нөлге тең (яғни мүлдем рефлекс болмайды). Геометриялық ұқсас рефлекстердің интенсивтіліктеріндегі айырмашылық элементар ұяшыққа кіретін ядролары әртүрлі зарядты z атомдардың шашырату қабілетінің әртүрлілігінен болады. Бұл айырмашылықты ескеру үшін кристалдан шашыраған сәулелердің интенсивтілігінің формуласына F_hkl құрылымдық амплитуданың екінші дәрежесіне тең F²_hkl құрылымдық фактор енгізіледі. Құрылымдық амплитуда – элементар ұяшықпен шашырау мәнін сипаттайтын, электрон өлшем бірліктерімен өрнектелген және бірдей жағдайда, яғни  және  бір мәніндегі электронның шашырауына қатысты шама. Әр hkl мәніне өз құрылымдық амплитуда мәні сәйкес келеді. Амлитуда келесі түрде өрнектеледі:

, (3.9)

мұнда х_j, y_j, z_j – ұяшықтағы j-нші базистік атомның координаталары, f_j - j-нші атомның атомдық шашыратушы факторы, N- базистік атомдар саны. Кристалдың бір элементар ұяшығымен шашыратылған толқынның амплитудасы электронмен шашыратылған толқынның амплитудасының және құрылымдық амплитуданың көбейтіндісіне тең. Кристалдық құрылымның кристаллографиялық ерекшеліктері құрылымдық факторға қатты әсер етеді: симметрия элементтеріне, тор түріне, симметрияның кеңістік тобына.

Өшулердің интегралды заңы

1. КЦК-тор. КЦК-тор базисі координаталары {{000}} {{ 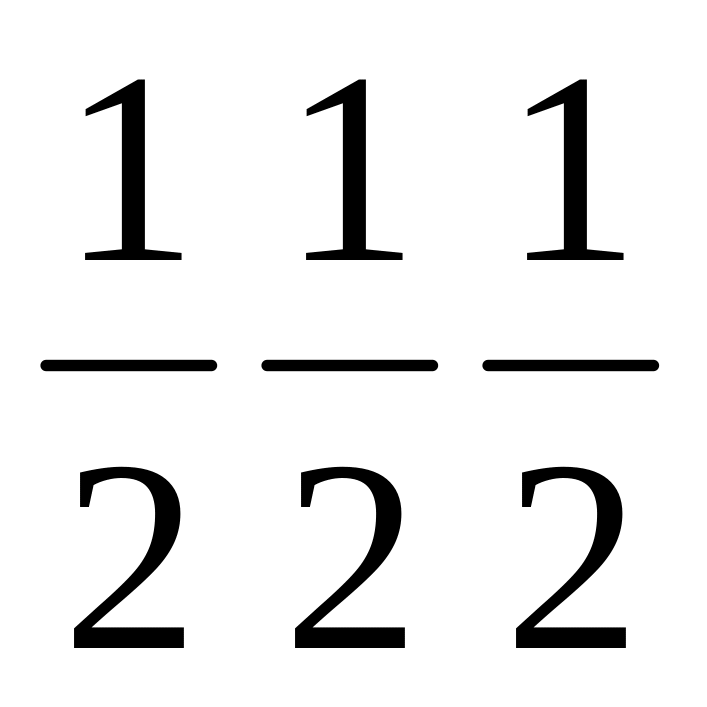}} екі бірдей атомнан тұрады, яғни атомдардың біреуі үшін х₁=y₁=z₁=0, ал екіншісі үшін х₂=y₂=z₂=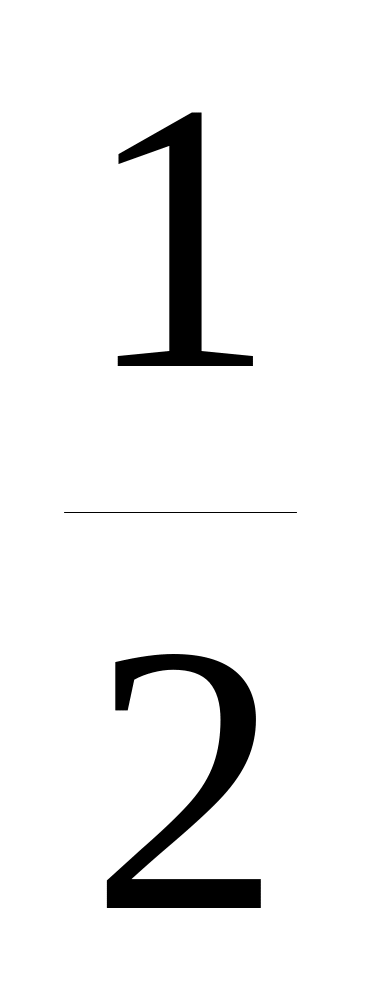 _. Онда құрылымдық фактор түрі: 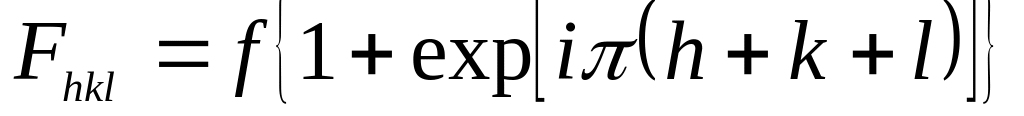, мұнда f-жеке атомның шашырату қабілеті. (h+k+l)-дің жұп мәнінде құрылымдық амплитуда нөлге тең емес. (h+k+l)-дің тақ мәнінде қосымша (h+k+l)/2 қосындылары экспонента таңбасын өзгертіп, фазаны 180⁰-ге өзгертеді. Бұл жағдайда амплитуда нөлге тең болып келеді. КЦК-құрылымы үшін индекстер қосындысы тақ болып келетін бүкіл hkl шағылулары өшеді. КЦК-торының дифференциалды бейнесінде (100) бағыты бойынша шағылулар болмауының физикалық мәні келесіде. Шағылу болу үшін бірінші және үшінші жазықтықтардан шағылған сәулелердің (олар элементар кубты шектеп тұрады) фазалар айырымы 2 болу қажет. КЦК-тордағы қосымша жазықтық бірінші және үшінші жазықтықтардың ортасында орналасқан. Одан шағылған сәуле фаза бойынша бірінші жазықтықтан шағылған сәуледен -ге ығысқан, сондықтан да сол бойынша шағылу бірінші жазықтықтан шағылуды өшіреді. Егер КЦК-тордағы жазықтықтар әртүрлі атомдардан тұрса, онда ондай өшу орын алмайды.

2. ЖЦК - тор. ЖЦК-тор базисі - координаталары келесі өрнекпен берілген төрт бірдей атомдан тұрады: {{000}}; {{0 1/2 1/2}}; {{1/2 0 1/2}}; {{1/2 1/2 0}}. Онда құрылымдық фактор түрі:

. (3.10)

Егер барлық (h+k), (h+l), (k+l) – тақ болса, онда бүкіл қосындылар модул және таңбасы бойынша бірдей болып келеді. Осы жағдай hkl-дың барлығы бірдей жұп болса, әлде барлығы тақ болса орын алады. Егер индекстер аралас болса, (біреулері – тақ, біреулері жұп болса), онда бұл жағдайда мүшелердің бір жұбы келесі жұпты жояды және құрылымдық амплитуда нөлге тең. Сонымен, ЖЦК-торында бүкіл аралас индекстері барлық hkl шағылуларын өшіреді.