Индивидуальные домашние задания

Вариант 1

1. Найти частные производные функции

2.Составьте уравнение касательной плоскости и нормали к поверхности, заданной уравнением F(x; y; z)=0 в указанной точке .

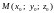3.Найдите точки экстремума функции .

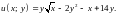
4.Найдите условный экстремум функции при заданном уравнении связи.

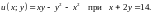
5.Найдите наибольшее и наименьшее значения функции в области , заданной указанными неравенствами.

6.Найти градиент функции в точке М.

7. Найти производную функции в точке А по направлению к точке В.

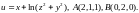
8. Заданы производственная функция (х - количество единиц первого ресурса, у – второго), цены единицы первого и второго ресурсов, а также ограничения I в сумме, которая может быть потрачена на приобретение ресурсов (сумма ). Найти величины используемых ресурсов , при которых фирма производитель получит наибольшую прибыль:

Вариант 2

1.Найти частные производные функции

2.Составьте уравнение касательной плоскости и нормали к поверхности, заданной уравнением F(x; y; z)=0 в указанной точке .

3.Найдите точки экстремума функции .

4. Найдите условный экстремум функции при заданном уравнении связи.

5. Найдите наибольшее и наименьшее значения функции в области , заданной указанными неравенствами.

6. Найти градиент функции в точке М.

7. Найти производную функции в точке А по направлению к точке В.

8. Потребитель имеет возможность потратить сумму 1000 (ден. ед.) на приобретение х единиц первого товара и у единиц второго товара. Заданы функция полезности и цены единицы соответственно первого и второго товаров. Найти значения , при которых полезность для потребителя будет наибольшей:

Вариант 3

1. Найти частные производные функции

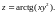
2.Составьте уравнение касательной плоскости и нормали к поверхности, заданной уравнением F(x; y; z)=0 в указанной точке .

.

3. Найдите точки экстремума функции .

;

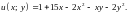4. Найдите условный экстремум функции при заданном уравнении связи.

5. Найдите наибольшее и наименьшее значения функции в области , заданной указанными неравенствами.

6. Найти градиент функции в точке М.

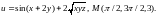
7. Найти производную функции в точке А по направлению к точке В.

8. Полезность от приобретения х единиц первого блага и у единиц второго блага имеет вид Единица первого блага стоит 2, а второго 3(ден.ед.). На приобретение этих благ планируется потратить 100 (ден.ед.). Как следует распределить эту сумму, чтобы полезность была наибольшей?

Вариант 4

1. Найти частные производные функции

2. Составьте уравнение касательной плоскости и нормали к поверхности, заданной уравнением F(x; y; z)=0 в указанной точке .

.

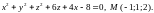3. Найдите точки экстремума функции .

;

4. Найдите условный экстремум функции при заданном уравнении связи.

5.Найдите наибольшее и наименьшее значения функции в области , заданной указанными неравенствами.

6. Найти градиент функции в точке М.

7. Найти производную функции в точке А по направлению к точке В.

8. Заданы производственная функция (х - количество единиц первого ресурса, у –второго), цены единицы первого и второго ресурсов, а также ограничения I в сумме, которая может быть потрачена на приобретение ресурсов (сумма ). Найти вели чины используемых ресурсов , при которых фирма производитель получит наибольшую прибыль:

Вариант 5

1. Найти частные производные функции

2. Составьте уравнение касательной плоскости и нормали к поверхности, заданной уравнением F(x; y; z)=0 в указанной точке .

3. Найдите точки экстремума функции .

4. Найдите условный экстремум функции при заданном уравнении связи.

5. Найдите наибольшее и наименьшее значения функции в области , заданной указанными неравенствами.

6. Найти градиент функции в точке М.

7. Найти производную функции в точке А по направлению к точке В.

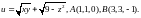
8. Потребитель имеет возможность потратить сумму 1000 (ден.ед.) на приобретение х единиц первого товара и у единиц второго товара. Заданы функция полезности и цены единицы соответственно первого и второго товаров. Найти значения , при которых полезность для потребителя будет наибольшей:

Вариант 6

1. Найти частные производные функции

2. Составьте уравнение касательной плоскости и нормали к поверхности, заданной уравнением F(x; y; z)=0 в указанной точке .

3. Найдите точки экстремума функции .

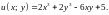
4. Найдите условный экстремум функции при заданном уравнении связи.

.

5. Найдите наибольшее и наименьшее значения функции в области , заданной указанными неравенствами.

6. Найти градиент функции в точке М.

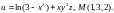
7. Найти производную функции в точке А по направлению к точке В.

8. Заданы производственная функция (х- количество единиц первого ресурса, у –второго), цены единицы первого и второго ресурсов, а также ограничения I в сумме, которая может быть потрачена на приобретение ресурсов (сумма ). Найти величины используемых ресурсов , при которых фирма производитель получит наибольшую прибыль:

Вариант 7

1. Найти частные производные функции

2. Составьте уравнение касательной плоскости и нормали к поверхности, заданной уравнением F(x; y; z)=0 в указанной точке . .

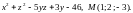3. Найдите точки экстремума функции .

;

4. Найдите условный экстремум функции при заданном уравнении связи.

5. Найдите наибольшее и наименьшее значения функции в области , заданной указанными неравенствами.

6. Найти градиент функции в точке М.

7. Найти производную функции в точке А по направлению к точке В.

8. Потребитель имеет возможность потратить сумму 221 (ден.ед.) на приобретение х единиц первого товара и у единиц второго товара. Заданы функция полезности и цены единицы соответственно первого и второго товаров. Найти значения , при которых полезность для потребителя будет наибольшей:

Вариант 8

1. Найти частные производные функции

2. Составьте уравнение касательной плоскости и нормали к поверхности, заданной уравнением F(x; y; z)=0 в указан точке .

3. Найдите точки экстремума функции .

4. Найдите условный экстремум функции при заданном уравнении связи.

5. Найдите наибольшее и наименьшее значения функции в области , заданной указанными неравенствами.

6. Найти градиент функции в точке М.

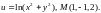
7. Найти производную функции в точке А по направлению к точке В.

8. Заданы производственная функция (х- количество единиц первого ресурса, у –второго), цены единицы первого и второго ресурсов, а также ограничения I в сумме, которая может быть потрачена на приобретение ресурсов (сумма ). Найти величины используемых ресурсов , при которых фирма производитель получит наибольшую прибыль:

Вариант 9

1. Найти частные производные функции

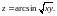
2. Составьте уравнение касательной плоскости и нормали к поверхности, заданной уравнением F(x; y; z)=0 в указанной точке .

3. Найдите точки экстремума функции .

4. Найдите условный экстремум функции при заданном уравнении связи.

5. Найдите наибольшее и наименьшее значения функции в области , заданной указанными неравенствами.

6. Найти градиент функции в точке М.

7. Найти производную функции в точке А по направлению к точке В.

8. Заданы производственная функция (х- количество единиц первого ресурса, у –второго), цены единицы первого и второго ресурсов, а также ограничения I в сумме, которая может быть потрачена на приобретение ресурсов (сумма ). Найти величины используемых ресурсов , при которых фирма производитель получит наибольшую прибыль:

Вариант 10

1. Найти частные производные функции

2. Составьте уравнение касательной плоскости и нормали к поверхности, заданной уравнением F(x; y; z)=0 в указанной точке .

3. Найдите точки экстремума функции .

4. Найдите условный экстремум функции при заданном уравнении связи.

5. Найдите наибольшее и наименьшее значения функции в области , заданной указанными неравенствами.

6. Найти градиент функции в точке М.

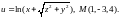
7. Найти производную функции в точке А по направлению к точке В.

8. Потребитель имеет возможность потратить сумму 174 (ден.ед.) на приобретение х единиц первого товара и у единиц второго товара. Заданы функция полезности и цены единицы соответственно первого и второго товаров. Найти значения , при которых полезность для потребителя будет наибольшей:

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Пискунов Н.С. Дифференциальное и интегральное исчисления/ Н.С. Пискунов.- М.: Наука, 2001. Т.1.- 250 с.

2. Сборник задач по математике для втузов. Ч.1. Линейная

алгебра и основы математического анализа. Под ред. А.В. Ефимова, Б.П.Демидовича.М.:Наука.1993.480 с.

3. Бутузов В.Ф. Математический анализ в вопросах и задачах. Функции нескольких переменных/ Бутузов В.Ф., Крутицкая Н.Ч., Медведев Г.Н., Шишкин А.А.- М.: Высш. Шк., 1988. 288с.

4. Зимина О.В. Высшая математика/ О.В. Зимина, А.И. Кириллов, Т.А. Сальникова.- М.: Физматлит, 2005.-368 с.

5. Рябушко А.П. Индивидуальные задания по высшей математике: учеб. пособие. В 4 ч. Ч.2. Комплексные числа. Неопределенные и определенные интегралы. Функции нескольких переменных. Обыкновенные дифференциальные уравнения/ А.П. Рябушко [и др.]. Минск:Выш. шк., 2007.-396 с.

6. Лунгу К.Н. Сборник задач по высшей математике. 1 курс/Лунгу К.Н., Письменный Д.Т. Федин С.Н., Шевченко Ю.А.-М.: Рольф, 2001.-576 с.

7. Красс М.С. Математика для экономистов: Учеб. пособие/ Красс М.С. , Чупрынов Б.П.- СПб.: Питер, 2009.-464с.

8. Кремер Н.Ш. Высшая математика для экономических специальностей: учебник и практикум/Н. Ш. Кремер, Б.П. Путко, И.М. Тришин, М.Н. Фридман; под ред. Н.Ш. Кремера.-М.: Изд. Юрайт; Высшее образование, 2010.-909 с.

СОДЕРЖАНИЕ

Введение………………………………………………………….1

1. Основные определения…..…………………………… ..2

2. Линии и поверхности уровня………………………… 5

3. Частное и полное приращение функции……………... 6

4. Предел и непрерывность функции нескольких

переменных…………………………………………………… .6

5. Частные производные функции нескольких переменных...........................................................................................11

6. Производная по направлению. Градиент....…………..14

7. Полный дифференциал функции нескольких переменных……………………........................……………………. ....17

8. Применение полного дифференциала к приближен-

ным вычислениям…................................................................…19

9.Геометрический смысл полного дифференциала. Касательная плоскость и нормаль к поверхности …………….. 20

10. Производные сложных функций………..………...... 22

11. Дифференциал сложной функции…………..……..... .25

12. Производные функций, заданных неявно ...………... 26

13. Частные производные различных порядков……...... 28

14. Дифференциалы высших порядков……............…..........31

15. Экстремум функции двух переменных……................33

16. Условный экстремум……..……………………............39

17. Наибольшее и наименьшее значения функции…......... 45

Индивидуальные домашние задания....................................49

БИБЛИОГРАФИЧЕСКИЙ СПИСОК…………………….....58

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

для организации самостоятельной работы

по изучению раздела «Функции нескольких переменных»

курса «Математика»

для студентов по направлению подготовки

бакалавров 230400 «Информационные системы и технологии».

очной формы обучения

бакалавров 080100 «Экономика»

очной формы обучения

Составители:

Глушко Елена Георгиевна

Максимова Екатерина Игоревна

В авторской редакции

ФГБОУ ВПО «Воронежский государственный

технический университет»