Учреждение образования Федерации профсоюзов Беларуси

Международный университет «МИТСО»

Кафедра логистики

Отчёт

по дисциплине: Экономико-математические методы и модели

Выполнил студент:

Гайдей Ольга Александровна

Этап 2, группа 1603з

Специальность: логистика

Проверил преподаватель:

кандидат физико-математических наук, доцент

Крачковский Александр Петрович

Задача 1 Задача о назначениях

Распределить пятерых работников между пятью работами, если затраты, обусловленные выполнением работ, приведены в таблице 1.

Таблица 1 – Затраты обусловленные выполнением работ

	В1	В2	В3	В4	В5
A1	4	5	7	4	6
A2	6	7	5	6	7
A3	6	5	6	5	6
A4	5	6	7	6	7
A5	7	5	6	5	6

Составить экономико-математическую модель и решить задачу с помощью надстройки «Поиск решения».

Решение:

Экономико-математическая модель:

Целевая функция:

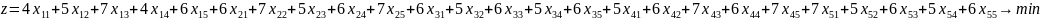
целевая функция будет стремиться к минимуму так как мы стремимся минимизировать наши затраты по выполнению работ.

Ограничения:

x_ij – равное 1 показывает, что i-го работника необходимо назначить на выполнение j-ой работы.

Экономико-математическая модель задачи составлена. Решим эту задачу с использованием надстройки Excel «Поиск решения».

На рисунке 1 представлен ход работы утилиты «Поиск решения».

Рисунок 1 – Ход работы утилиты Поиск решения

На рисунке 2 представлен результат решения задачи.

Рисунок 2 – Результат решения задачи

Вывод: из рисунка 2 следует, что для того, чтобы общая величина затрат была минимальной необходимо для выполнения работы А1 назначить работника В4, А2 – В3, А3 – В5, А4 – В1, А5 – В2, при этом суммарные затраты будут минимальны и составят 25 ед.

Задача 2 Транспортная задача

Исходная информация транспортной задачи представлена в таблице 2.

Таблица 2 – Исходные данные

	В1	В2	В3	В4	Запасы
А1	3	6	5	2	40
А2	3	4	8	8	40
А3	4	3	6	1	40
Потребности	30	27	30	30

Определить:

1. приближенный план, схему перевозок, а также его стоимость методом северо-западного угла;

2. приближенный план, схему перевозок, а также его стоимость методом минимального элемента;

3. оптимальный план, схему перевозок, а также его стоимость с помощью надстройки «Поиск решения».

Решение:

1. Метод северо-западного угла

Проверим необходимое и достаточное условие разрешимости задачи.

Как видно, суммарная потребность груза в пунктах назначения меньше запасов груза на базах. Следовательно, модель исходной транспортной задачи является открытой. Чтобы получить закрытую модель, введем дополнительную (фиктивную) потребность, равной 3 (120—117). Тарифы перевозки единицы груза из базы во все магазины полагаем равны нулю.

Занесем исходные данные в распределительную таблицу 3.

Таблица 3 – Распределительная таблица

	В1	В2	В3	В4	В5	Запасы
А1	3	6	5	2	0	40
А2	3	4	8	8	0	40
А3	4	3	6	1	0	40
Потребности	30	27	30	30	3

Первый опорный план начинается заполняться с верхнего левого угла (таблица 4).

Таблица 4 – Опорный план 1

	В1			В2			В3			В4			В5					Запасы
А1	30			10												u1=0		40
		3			6			5			2			0
А2				17			23									u2=-2		40
		3			4			8			8			0
А3							7			30			3			u3=-4		40
		4			3			6			1			0
	v1=3			v2=6			v3=10			v4=5			v5=4
Потребности	30			27			30			30			3

В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.

Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n - 1 = 7. Следовательно, опорный план является невырожденным.

Значение целевой функции для этого опорного плана равно:

F(x) = 3*30 + 6*10 + 4*17 + 8*23 + 6*7 + 1*30 + 0*3 = 474

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.

u₁+ v₁= 3; 0 + v₁ = 3; v₁ = 3

u₁ + v₂ = 6; 0 + v₂ = 6; v₂ = 6

u₂ + v₂ = 4; 6 + u₂ = 4; u₂ = -2

u₂ + v₃ = 8; -2 + v₃ = 8; v₃ = 10

u₃ + v₃ = 6; 10 + u₃ = 6; u₃ = -4

u₃ + v₄ = 1; -4 + v₄ = 1; v₄ = 5

u₃ + v₅ = 0; -4 + v₅ = 0; v₅ = 4

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_j > c_ij

(1;3): 0 + 10 > 5; ∆₁₃ = 0 + 10 - 5 = 5

(1;4): 0 + 5 > 2; ∆₁₄ = 0 + 5 - 2 = 3

(1;5): 0 + 4 > 0; ∆₁₅ = 0 + 4 - 0 = 4

(2;5): -2 + 4 > 0; ∆₂₅ = -2 + 4 - 0 = 2

max(5,3,4,2) = 5

Выбираем максимальную оценку свободной клетки (1;3): 5

Для этого в перспективную клетку (1;3) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-» (таблица 5).

Таблица 5 – Цикл 1

	В1			В2			В3			В4			В5
А1	30			10												u1=0
		3	-		6	+		5			2			0
А2				17			23									u2=-2
		3	+		4	-		8			8			0
А3							7			30			3			u3=-4
		4			3			6			1			0
	v1=3			v2=6			v3=10			v4=5			v5=4

Цикл приведен в таблице (1,3 → 1,2 → 2,2 → 2,3).

Из грузов х_ij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (1, 2) = 10. Прибавляем 10 к объемам грузов, стоящих в плюсовых клетках и вычитаем 10 из Х_ij, стоящих в минусовых клетках. В результате получим новый опорный план (таблица 6).

Таблица 6 – Опорный план 2

	В1		В2		В3		В4		В5
А1	30				10						u1=0
		3		6		5		2		0
А2			27		13						u2=3
		3		4		8		8		0
А3					7		30		3		u3=1
		4		3		6		1		0
	v1=3		v2=1		v3=5		v4=0		v5=-1

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.

u₁ + v₁ = 3; 0 + v₁ = 3; v₁ = 3

u₁ + v₃ = 5; 0 + v₃ = 5; v₃ = 5

u₂ + v₃ = 8; 5 + u₂ = 8; u₂ = 3

u₂ + v₂ = 4; 3 + v₂ = 4; v₂ = 1

u₃ + v₃ = 6; 5 + u₃ = 6; u₃ = 1

u₃ + v₄ = 1; 1 + v₄ = 1; v₄ = 0

u₃ + v₅ = 0; 1 + v₅ = 0; v₅ = -1

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_j > c_ij

(2;1): 3 + 3 > 3; ∆₂₁ = 3 + 3 - 3 = 3

(2;5): 3 -1 > 0; ∆₂₅ = 3 -1 - 0 = 2

max(3,2) = 3

Выбираем максимальную оценку свободной клетки (2;1): 3

Для этого в перспективную клетку (2;1) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-» (таблица 7).

Таблица 7 – Цикл 2

	В1			В2			В3			В4			В5
А1	30						10									u1=0
	-	3			6	+					2			0
А2				27			13									u2=3
	+	3			4	-					8			0
А3							7			30			3			u3=1
		4			3			6			1			0
	v1=3			v2=1			v3=5			v4=0			v5=-1

Цикл приведен в таблице (2,1 → 2,3 → 1,3 → 1,1).

Из грузов х_ij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (2, 3) = 13. Прибавляем 13 к объемам грузов, стоящих в плюсовых клетках и вычитаем 13 из Х_ij, стоящих в минусовых клетках. В результате получим новый опорный план 3 (таблица 8).

Таблица 8 – Опорный план 3

	В1			В2			В3			В4			В5
А1	17						23									u1=0
		3			6			5			2			0
А2	13			27												u2=0
		3			4			8			8			0
А3							7			30			3			u3=1
		4			3			6			1			0
	v1=3			v2=4			v3=5			v4=0			v5=-1

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁= 0.

u₁ + v₁ = 3; 0 + v₁ = 3; v₁ = 3

u₂ + v₁ = 3; 3 + u₂ = 3; u₂ = 0

u₂ + v₂ = 4; 0 + v₂ = 4; v₂ = 4

u₁ + v₃ = 5; 0 + v₃ = 5; v₃ = 5

u₃ + v₃ = 6; 5 + u₃ = 6; u₃ = 1

u₃ + v₄ = 1; 1 + v₄ = 1; v₄ = 0

u₃ + v₅ = 0; 1 + v₅ = 0; v₅ = -1

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_j > c_ij

(3;2): 1 + 4 > 3; ∆₃₂ = 1 + 4 - 3 = 2

Выбираем максимальную оценку свободной клетки (3;2): 3

Для этого в перспективную клетку (3;2) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-» (таблица 9).

Таблица 9 – Цикл 3

	В1			В2			В3			В4			В5
А1	17						23									u1=0
	-	3			6	+		5			2			0
А2	13			27												u2=0
	+	3	-		4			8			8			0
А3							7			30			3			u3=1
		4	+		3	-		6			1			0
	v1=3			v2=4			v3=5			v4=0			v5=-1

Цикл 3 приведен в таблице (3,2 → 3,3 → 1,3 → 1,1 → 2,1 → 2,2).

Из грузов х_ij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (3, 3) = 7. Прибавляем 7 к объемам грузов, стоящих в плюсовых клетках и вычитаем 7 из Х_ij, стоящих в минусовых клетках. В результате получим новый опорный план 4.

Таблица 10 – Опорный план 4

	В1			В2			В3			В4			В5
А1	10						30									u1=0
		3			6			5			2			0
А2	20			20												u2=0
		3			4			8			8			0
А3				7						30			3			u3=-1
		4			3			6			1			0
	v1=3			v2=4			v3=5			v4=2			v5=1

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁= 0.

u₁ + v₁ = 3; 0 + v₁ = 3; v₁ = 3

u₂ + v₁ = 3; 3 + u₂ = 3; u₂ = 0

u₂ + v₂ = 4; 0 + v₂ = 4; v₂ = 4

u₃ + v₂ = 3; 4 + u₃ = 3; u₃ = -1

u₃ + v₄ = 1; -1 + v₄ = 1; v₄ = 2

u₃ + v₅ = 0; -1 + v₅ = 0; v₅ = 1

u₁ + v₃ = 5; 0 + v₃ = 5; v₃ = 5

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_j > c_ij

(1;5): 0 + 1 > 0; ∆₁₅ = 0 + 1 - 0 = 1

(2;5): 0 + 1 > 0; ∆₂₅ = 0 + 1 - 0 = 1

max(1,1) = 1

Выбираем максимальную оценку свободной клетки (1;5): 0

Для этого в перспективную клетку (1;5) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-» (таблица 11).

Таблица 11 – Цикл 4

	В1			В2			В3			В4			В5
А1	10						30									u1=0
	-	3			6			5			2	+		0
А2	20			20												u2=0
	+	3	-		4			8			8			0
А3				7						30			3			u3=-1
		4	+		3			6			1	-		0
	v1=3			v2=4			v3=5			v4=2			v5=1

Цикл 4 приведен в таблице (1,5 → 1,1 → 2,1 → 2,2 → 3,2 → 3,5).

Из грузов х_ij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (3, 5) = 3. Прибавляем 3 к объемам грузов, стоящих в плюсовых клетках и вычитаем 3 из Х_ij, стоящих в минусовых клетках. В результате получим новый опорный план 5 (таблица 12).

Таблица 12 – Опорный план 5

	В1			В2			В3			В4			В5
А1	7						30						3			u1=0
		3			6			5			2			0
А2	23			17												u2=0
		3	-		4			8			8			0
А3				10						30						u3=-1
		4			3			6			1			0
	v1=3			v2=4			v3=5			v4=2			v5=0

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁= 0.

u₁ + v₁ = 3; 0 + v₁ = 3; v₁ = 3

u₂ + v₁ = 3; 3 + u₂ = 3; u₂ = 0

u₂ + v₂ = 4; 0 + v₂ = 4; v₂ = 4

u₃ + v₂ = 3; 4 + u₃ = 3; u₃ = -1

u₃ + v₄ = 1; -1 + v₄ = 1; v₄ = 2

u₁ + v₃ = 5; 0 + v₃ = 5; v₃ = 5

u₁ + v₅ = 0; 0 + v₅ = 0; v₅ = 0

Опорный план 5 является оптимальным, так все оценки свободных клеток удовлетворяют условию u_i + v_j ≤ c_ij.

Минимальные затраты составят:

F(x) = 3*7 + 5*30 + 0*3 + 3*23 + 4*17 + 3*10 + 1*30 = 368

Схема перевозок:

из 1-го склада необходимо груз направить 1-му потребителю в количестве 7 ед., 3-му потребителю в количестве 30 ед.;

из 2-го склада необходимо груз направить 1-му потребителю – 23 ед., 2-му потребителю – 17ед.;

из 3-го склада необходимо груз направить второму потребителю – 10 ед., 4-му – 30 ед.

На 1-ом складе остался невостребованным груз в количестве 3 ед.

Оптимальный план является вырожденным, так как базисная переменная x₁₅=0.