Вариационное исчисление и методы оптимизации

1. Простейшие задачи вариационного исчисления. Уравнение Эйлера. Основные понятия и определения. Основная лемма вариационного исчисления. Простейшая задача вариационного исчисления. Вариация для функционала 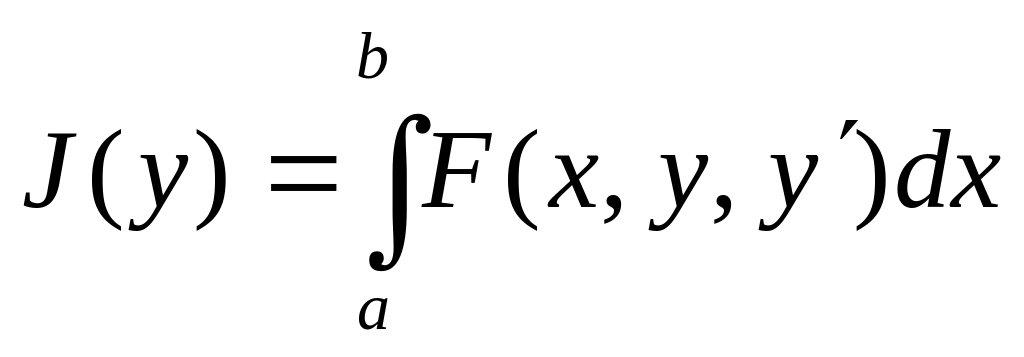. Уравнение Эйлера.

2. Некоторые обобщения простейшей вариационной задачи. Вариационная задача для функционала . Вариационная задача для функционала . Задачи с подвижными границами. Замечания о достаточных условиях экстремума функционала. Понятие о второй вариации функционала.

3. Вариационные задачи на множестве функций нескольких аргументов. Понятие о вариационном принципе в вариационных моделях. Вариационные задачи для функционала вида 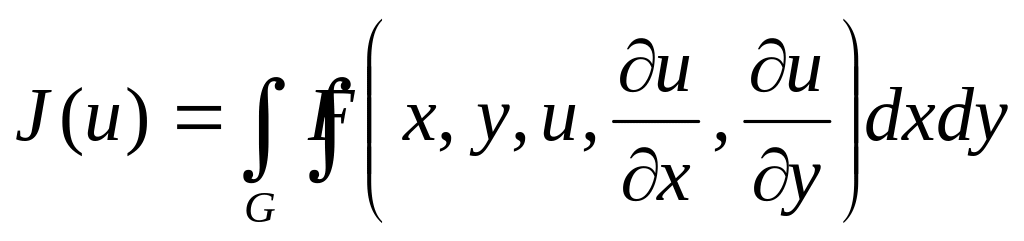. Уравнение Эйлера-Остроградского. Теорема о минимуме квадратичного функционала.

4. Задачи на условный экстремум. Формулировка задачи. Основные определения и теоремы. Задача на условный экстремум для функционал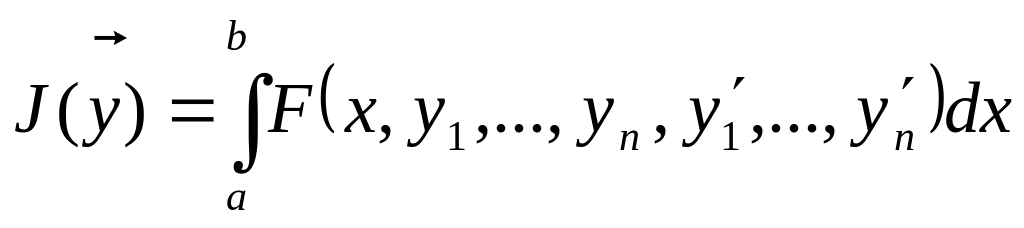а . Вариационная задача Лагранжа. Изопериметрическая задача.

Теория чисел

1. Делимость в кольце Z и числовые сравнения. Деление целых чисел с остатком. Отношение делимости. Наибольший общий делитель и наименьшее общее кратное чисел, их нахождение. Простые и составные числа. Основная теорема арифметики о разложении целых чисел на простые сомножители. Отношение сравнимости целых чисел по модулю и его основные свойства. Классы вычетов и операции над ними. Кольцо классов вычетов. Полная и приведенная системы вычетов. Теоремы Эйлера и Ферма. Поле классов вычетов по простому модулю.

2. Цепные дроби. Конечные цепные дроби и рациональные числа. Подходящие дроби; их свойства. Бесконечные цепные дроби. Подходящие дроби как наилучшие приближения действительных чисел. Приложения цепных дробей.

3. Линейные сравнения и неопределенные уравнения первой степени. Критерий разрешимости и число решений линейного сравнения. Основные методы решения линейных сравнений (метод подбора, метод преобразования коэффициентов, метод Эйлера, применение цепных дробей для решения линейных сравнений). Неопределенные уравнения первой степени и их связь с линейными сравнениями.

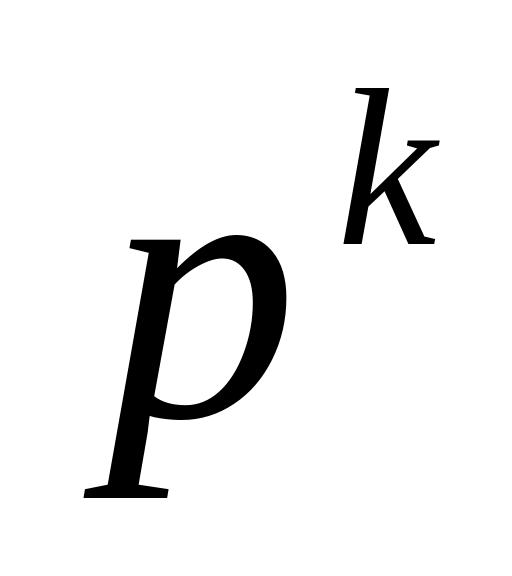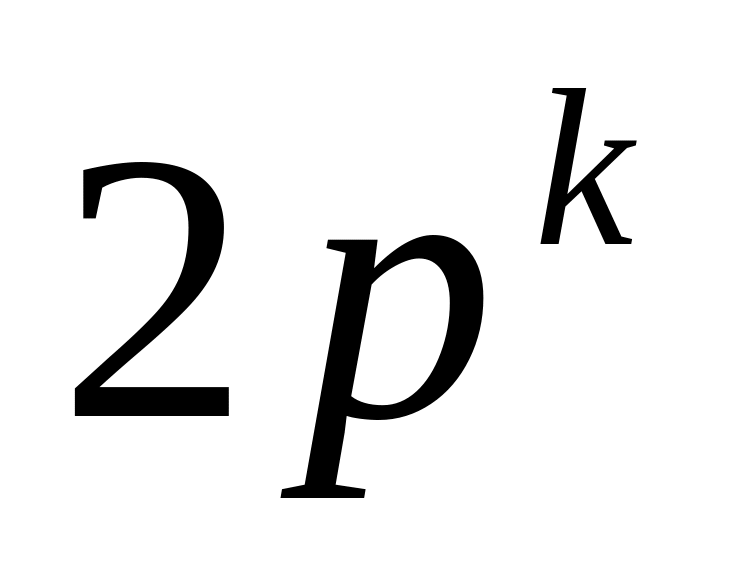4. Первообразные корни и индексы. Показатель числа по заданному модулю. Первообразные корни. Теорема о существовании первообразного корня по простому модулю. Первообразные корни по модулям и . Теорема об отыскании первообразных корней. Индексы и их свойства. Дискретное логарифмирование и его применение к решению двучленных сравнений по простому модулю.

Нейросетевые технологии обработки информации

1. Компьютеры и мозг. Принципы обработки информации мозгом; мозг, компьютеры и нейрокомпьютеры; эволюция компьютеров. Биологический и формальный нейрон: биологические основы функционирования нейрона; математическая модель нейрона Мак-Калока и Питса.

2. Типы и модели нейронов. Архитектура персептрона, модель сигмоидального нейрона, обучение персептрона и сигмоиадального нейрона. Нейрон типа “адалайн”, инстар и оутстар Гроссберга: структурная схема нейрона типа “адалайн; адаптивный подбор весовых коэффициентов. Нейроны типа WTA, модель нейрона Хебба: правила Видроу-Хоффа, недостатки метода; градиентные методы обучения нейрона. Модель нейрона Хебба: структурная схема нейрона Хебба, правило обучения, модифицированное правило Ойя; стохастическая модель нейрона.

3. Методика решения задач в нейросетевом логическом базисе: классификация нейронных сетей, методика синтеза алгоритмов адаптации многослойных нейронных сетей.

4. Метод обратного распространения ошибки: решение задач при помощи нейронных сетей, алгоритм обратного распространения ошибки. Нейронные сети радиально-базисных функций: архитектура и правила задания RBF-сети, обучение RBF-сети, сравнение многослойного персептрона и RBF-сетей. Вероятностная и обобщённо-регрессионная нейронные сети: архитектура и обучение вероятностной нейронной сети, структура и обучение обобщенно-регрессионной нейронной сети, классы решаемых задач.

5. Нейронная сеть Кохонена: соревновательный слой нейронов, алгоритм самообучения, сходимость процесса самообучения и негативные эффекты. Самоорганизующаяся карта Кохонена: архитектура топографической карты, методика построения карты, выбор числа нейронов карты, интерпретации результатов построения карты.

6. Нейронная сеть Хопфилда: структурная схема нейронной сети Хопфилда, алгоритм функционирования нейронной сети Хопфилда.

7. Нейронная сеть Хэмминга: структура нейронной сети Хэмминга, алгоритм функционирования сети Хэмминга. Гибридные нейронные сети: основные понятия и определения гибридных сетей; алгоритмы обучения и использования гибридных сетей.