1.3.1. Дискретизация

Рассмотрим процедуру дискретизации детерминированных изображений. При анализе систем дискретизации и восстановления непрерывных изображений, обрабатываемые изображения обычно представляются как детерминированные поля.

Если входное изображение представить в виде непрерывной функции , представляющей распределение яркости или другого параметра реального изображения, то процедура дискретизации такого изображения может рассматриваться как перемножение этой функции с некоторой пространственно-дискретизирующей функцией :

, (1.1)

где значения -функции задаются в узлах решётки с шагом (рис. 1.6).

Спектр дискретизирующей функции можно получить путём двумерного преобразования Фурье (ДПФ):

. (1.2)

Это преобразование приводит к формированию набора -функций в плоскости пространственных частот с шагом , . Низкие пространственные частоты соответствуют медленным изменениям яркости изображения по пространственным координатам, а высокие пространственные частоты – быстрым изменениям яркости, т.е. мелким деталям изображения и резким перепадам яркости на границах объектов.

Рис.1.8 Пространственно-дискретизирующая функция

Рис. 1.9 Спектр дискретизиро-ванного изображения

Тогда дискретизированное изображение будет описываться:

. (1.3)

Для анализа процессов дискретизации удобно использовать спектр, получаемый в результате непрерывного ДПФ для дискретного изображения:

. (1.4)

Этот спектр можно представить в виде свёртки спектра исходного изображения и спектра дискретизирующей функции:

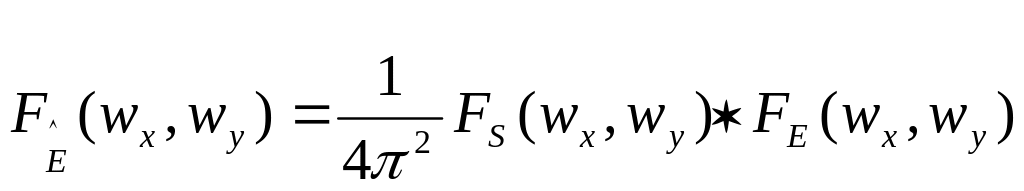. (1.5)

Определив спектр как свёртку и учитывая свойства -функции, можно получить:

. (1.6)

Как видно из полученного выражения, спектр дискретного изображения представляет собой бесконечное повторение в плоскости , спектра исходного изображения, причём шаг сдвига по осям составляет и (рис.1.9). При увеличении шага сдвига возможно перекрытие соседних спектров, что приводит к существенным помехам на изображении после восстановления.

На рис. 1.10 показан случай, когда в результате дискретизации побочные спектры не пересекаются с основным. Такой случай имеет место при достаточно больших пространственных частотах дискретизации по обеим координатам. В таком случае возможно восстановление исходного изображения по дискретизированному с применением пространственного фильтра, выделяющего спектр исходного изображения из спектра дискретизированного изображения. Это является обобщением теоремы Котельникова на двумерные сигналы.

Рис.1.10. Пространственные спектры дискретизированного изображения в случае выполнения условий аналога теоремы Котельникова для двумерных сигналов

Рис.1.11. Пространственные спектры дискретизированного изображения в случае невыполнения условий аналога теоремы Котельникова для двумерных сигналов

На рис.1.11 показан случай, когда побочные спектры перекрываются со спектром исходного изображения, что является следствием недостаточно больших частот дискретизации по пространственным координатам. В этом случае восстановление исходного изображения по дискретизированному без искажений невозможно.

Если частота дискретизации изображения недостаточна и возникают перекрытия спектров, то в восстановленном изображении, даже при идеальных характеристиках восстанавливающих фильтров, синтезируются ложные пространственные гармоники, которые приводят к появлению ложных узоров (муар-эффект). Для уменьшения этих нежелательных эффектов используют низкочастотную фильтрацию исходного изображения.

Рис.1.12 (а) Восьмибитное изображение 1024х1024. (б) 512х512. (в) 256х256. (г) 128х128. (д) 64х64. (е) 32х32. Изображения (б)-(е) увеличены до размеров 1024х1024 дублированием строк и столбцов.

Сравнивая рис.1.12 (а) с изображением рис.1.12 (б) можно заметить, что их практически невозможно различить. Потеря степени детализации слишком мала, чтобы её можно было увидеть на печатной странице, при том масштабе, что используется на рисунке. Следующее изображение на рис.1.12 (в) демонстрирует очень слабую ступенчатость на границах между лепестками цветка и черным фоном. Начинает также появляться слегка более выраженная зернистость по всему полю изображения. Эти эффекты становятся ещё более заметными в изображении на рис.1.12 (г) и совершенно отчетливы в изображениях 64х64 и 32х32.

Чтобы искажений, вызванных дискретизацией, не возникало, необходимо выбирать достаточно большие пространственные частоты для дискретизации по обеим координатам. Однако если рассматривать этот процесс в телевидении (при передаче изображения в цифровой телевизионной системе осуществляется двумерная дискретизация; при этом дискретизация по вертикальной координате выполняется уже в оптико-электронном преобразователе путём разложения передаваемого кадра на строки, т.е. эта операция имеется уже в аналоговом телевидении; дискретизация по горизонтальной координате выполняется путём дискретизации видеосигнала во времени), эти пространственные частоты фактически предопределены параметрами, задаваемыми в используемой стандартом разложения, т.е. количеством строк и количеством элементов в каждой строке. Для согласования пространственного спектра изображения с указанными параметрами во многих случаях приходится ограничивать верхние граничные пространственные частоты изображения перед дискретизацией. Эта операция выполняется с помощью специальных оптических рассеивающих элементов, располагаемых перед ПЗС-матрицей (прибор с зарядовой связью), или просто путём небольшой расфокусировки объектива в телевизионной камере.