2.7.4 Соотношения между коэффициентами Эйнштейна

Эйнштейн рассмотрел процессы в полости абсолютно черного тела, в которой находятся атомы газа. Со стенок, ограничивающих полость абсолют­но черного тела, происходит тепловое излучение электромагнитного поля, вследствие чего в полости устанавливается некоторая плот­ность энергии этого поля П_. Под действием этого поля атомы газа со­вершают вынужденные переходы; кроме того, происходят и спонтан­ные переходы. Эйнштейн рассмотрел состояние термодинамическо­го равновесия такой системы. Состоянием термодинамического рав­новесия называется такое, в которое она приходит, будучи предостав­ленной сама себе. В этом состоянии плотность энергии электромаг­нитного поля в полости абсолютно черного тела, находящегося при температуре Т, определяется формулой Планка

(2.40)

Распределение атомов газа по уровням энергии в состоянии термо­динамического равновесия подчиняется закону Больцмана

. (2.41)

При этом число излучательных переходов в единицу времени с верхних уровней на нижние должно равняться числу безызлучательных переходов с нижних уровней на верхние. Рассмотрим переходы ме­жду двумя уровнями Е₂ и Е₁. С уровня Е₂ совершаются спонтанные переходы с вероятностью в единицу времени А₂₁ и вынужденные пе­реходы под действием поля излучения стенок полости с вероятно­стью E₂₁ = B₂₁ П_. Полное число переходов в единицу времени со второго на первый уровень N₂₁ будет

N₂₁ = N₂ (A₂₁ + Е₂₁) = N₂ (A₂₁ + B₂₁ П_). (2.42)

С первого уровня на второй будут совершаться только вынужден­ные переходы, число которых в единицу времени:

N₁₂ = N₁B₁₂П_. (2.43)

В состоянии равновесия

N₂ (A₂₁ + Е₂₁) = N₁ Е₁₂. (2.44)

При условии B₁₂ = B₂₁

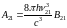. (2.45)

В приборах СВЧ-диапазона, работающих на «низкой» частоте, вероятность спонтанных переходов мала по сравнению с вероят­ностью вынужденных переходов и их роль невелика. В лазерах же, работающих на оптических частотах, пренебрегать спонтанными переходами нельзя.

2.7.5 Релаксационные переходы

Переход системы частиц в состо­яние термодинамического равновесия называется процессом ре­лаксации, а квантовые переходы, которые способствуют установ­лению и поддержанию термодинамического равновесия, называ­ются релаксационными переходами. В качестве примера, иллюст­рирующего релаксационные переходы, рассмотрим процессы в не­котором объеме газа. Как известно, молекулы газа находятся в теп­ловом хаотическом движении, причем средняя кинетическая энер­гия молекулы газа пропорциональна KT (K – постоянная Больцмана, Т – абсолютная температура газа). В процессе теплового хаоти­ческого движения молекулы газа сталкиваются между собой. При этом сталкивающиеся частицы могут взаимодействовать между собой либо упруго, т.е. без изменения суммарной кинетической энергии сталкивающихся частиц, либо неупруго, когда часть кине­тической энергии одной частицы может перейти во внутреннюю Энергию другой (или наоборот: внутренняя энергия одной частицы может перейти в кинетическую энергию другой). В состоянии тер­модинамического (теплового) равновесия температура газа и сум­марная кинетическая энергия всех частиц остаются неизменными. Неизменна и внутренняя энергия частиц, которая распределяется между уровнями по закону Больцмана.

Если нарушить равновесие, например, резко увеличить тем­пературу газа до величины T₂, то при новой температуре сред­няя кинетическая энергия молекул газа возрастет (станет про­порциональна KT₂), суммарная кинетическая энергия всех час­тиц газа возрастет, а внутренняя энергия частиц некоторое вре­мя будет оставаться неизменной. В результате неупругих соударении, при которых часть кинетической энергии молекул перехо­дит во внутреннюю энергию частиц, произойдет ее увеличение так, что установится новое распределение частиц по энергиям. После установления нового равновесия внутренняя энергия рас­пределяется по закону Больцмана при температуре Т₂. Постоянная времени установления процесса релаксации назы­вается временем релаксации _рел.

Релаксационные процессы происходят не только в газах, но и в твердых телах. Переход кинетической энергии одной частицы во внутреннюю энергию другой при неупругих столкновениях молекул газа является примером релаксационных переходов. Релаксаци­онные переходы носят статистический характер. Вероятности ре­лаксационных переходов между уровнями Е₁ и Е₂ будем обозна­чать Е₁₂, а обратных переходов Е₂₁. В большинстве случаев, име­ющих место в квантовых приборах, релаксационные переходы яв­ляются безызлучательными.

В состоянии термодинамического равновесия населенности уровней не изменяются во времени, поэтому число безызлучательных переходов с уровня 1 на уровень 2 в 1 с равно числу обратных безызлучательных переходов с уровня 2 на уровень 1

N_1БE₁₂ = N_2БE₂₁. (2.46)

В состоянии термодинамического равновесия распределение населенностей определяется законом Больцмана. Получаем

E₂₁ / E₁₂ = exp (h₂₁ / KT). (2.47)

Из этого следует, что вероятность безызлучательных пере­ходов сверху вниз больше, чем снизу вверх (E₂₁ > E₁₂) в отличие от вероятностей вынужденных переходов, которые одинаковы. Если h₂₁ << KT, что обычно справедливо для квантовых прибо­ров СВЧ-диапазона, то можно заменить приближенным выражением

E₂₁ / E₁₂ = 1 + h₂₁ / KT. (2.48)