Глава 2. Неконсервативная система с двумя степенями свободы
2.1.Уравнения движения и имитационная модель
Линейные уравнения колебаний систем с конечным числом степеней свободы при одном параметрическом возбуждении могут быть записаны в виде
,
(2.1)
где
и
симметричные, положительно определенные
постоянные матрицы;
единичная
матрица;
постоянная
матрица произвольной структуры,
характеризующая структуру параметрического
возбуждения. Как и в первом случаи
проведем численное исследование влияния
структуры коэффициентов возбуждения
на положение границ параметрического
резонанса. Исследование проведем с
помощью схемы имитационного моделирования,
представленной на рисунке 2.1.
Рисунок 2.1 Блок-схема имитационного моделирования для исследования параметрических колебаний системы с двумя степенями свободы
Для вычислений примем
.
(2.2)
Кроме
того, принято, что
,
,
.
Области параметрического резонанса
построены на рисунках 2.2 – 2.5 соответственно
для матрицы
,
имеющей следующие значения
.
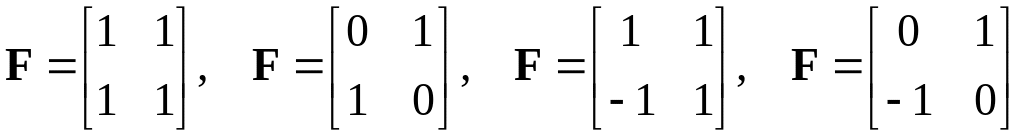(2.3)
Рисунок
2.2 Области
параметрического резонанса для системы
с двумя степенями свободы при
Рисунок
2.3 Области
параметрического резонанса для системы
с двумя степенями свободы при
Рисунок
2.4 Области
параметрического резонанса для системы
с двумя степенями свободы при
Рисунок
2.5 Области
параметрического резонанса для системы
с двумя степенями свободы при
При отсутствии демпфирования первые два случая соответствуют каноническим системам.
На
рисунке 2.2 кроме главных и простых
кратных параметрических резонансов
присутствуют комбинационные резонансы
суммарного типа
.
Для системы, области неустойчивости
которой, представлены на рисунке 2.3
главные параметрические резонансы на
частотах
и
отсутствуют. Наиболее представительной
здесь является область неустойчивости
суммарного типа
.
Для неканонических систем области
неустойчивости могут иметь «островной»
характер, как это видно из рисунка 2.4.
Для данного случая имеют место простые
главные резонансы
и
и параметрический резонанс разностного
типа
.
Этот резонанс превалирует и для четвертого
случая матрицы
(рисунок 2.5), где наблюдаются также и
резонансы на частотах
и
.
2.2. Построение областей неустойчивости.
Были проведены также исследования параметрических резонансов для системы, нагруженной постоянной по величине позиционными неконсервативными силами . Уравнение движения такой системы возьмем в виде
.
(2.4)
Здесь
,
,
.
Как и ранее принято
,
.
Критическое значение параметра
неконсервативной нагрузки
при
,
соответствующее потери устойчивости
тривиального решения уравнения (2.4),
определяется по формуле
.
(2.5)
Блок – схема имитационного моделирования для рассматриваемой системы представлена на рисунке 2.6.
Рисунок 2.6 Блок-схема имитационного моделирования для исследования параметрических колебаний неконсервативной системы с двумя степенями свободы
Определение
границ параметрического резонанса
проведем для случаев, когда параметр
неконсервативной нагрузки составляет:
(рисунок 2.7),
(рисунок 2.8),
(рисунок 2.9),
(рисунок 2.10) и
(рисунок 2.11). При этом проследим за
видоизменением границ параметрического
резонанса, построенных на рисунке 2.5.
Уже при малых значениях
(рисунок 2.7) появляется дополнительная
серповидная область неустойчивости в
окрестности частот, соответствующих
главным параметрическим резонансам
и
.
С ростом параметра
(рисунки 2.8 и 2.9) эта область увеличивается,
несколько прижимая к оси абсцисс границу
основной области неустойчивости. Картина
кардинально меняется при достижении
параметром
своего критического значения (рисунок
2.10) и превышает его (рисунок 2.11). Здесь
уже речь может идти о параметрической
стабилизации динамически неустойчивых
систем. Области устойчивого тривиального
решения уравнения (2.8), сужающиеся с
ростом
,
сдвигаются в сторону больших значений
амплитуды параметрического воздействия.
Рисунок
2.7 Области
неустойчивости для неконсервативной
системы с двумя степенями свободы при
Рисунок
2.8 Области
неустойчивости для неконсервативной
системы с двумя степенями свободы при
Рисунок
2.9 Области
неустойчивости для неконсервативной
системы с двумя степенями свободы при
Рисунок
2.10 Области
неустойчивости для неконсервативной
системы с двумя степенями свободы при
Рисунок
2.11 Области
неустойчивости для неконсервативной
системы с двумя степенями свободы при
