3.2 Построение областей неустойчивости и параметрического резонанса

Для исследования устойчивости тривиального решения уравнения (3.6) составим уравнения в вариациях относительно вектора малых отклонений от положения равновесия

, (3.8)

где введены следующие обозначения

, , , ,

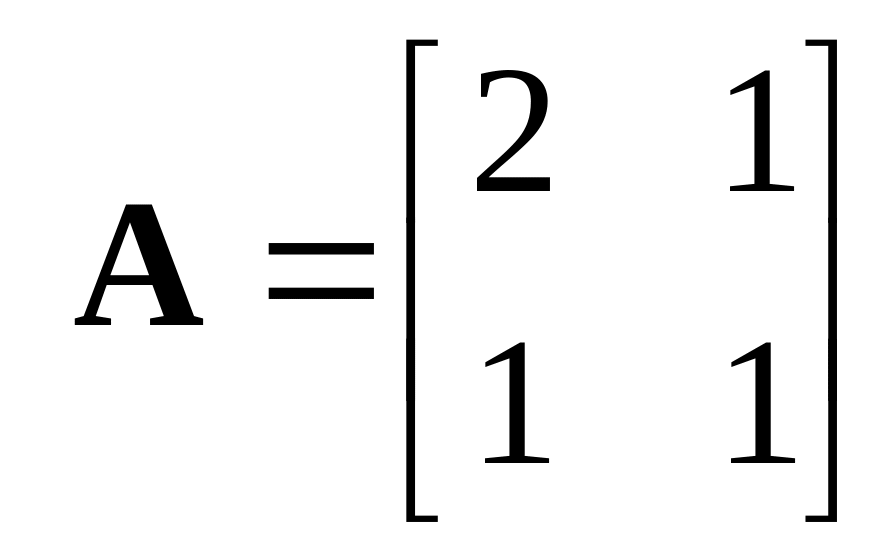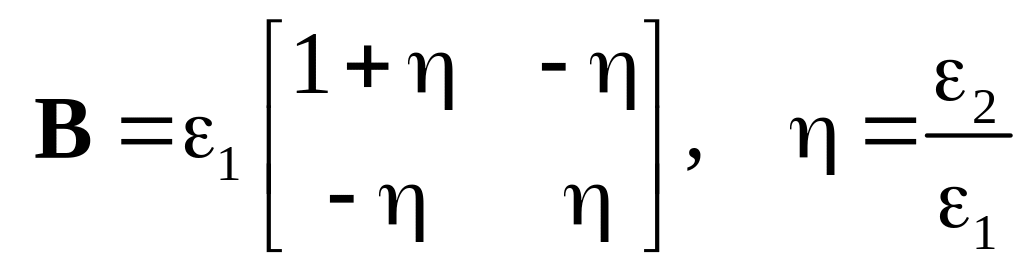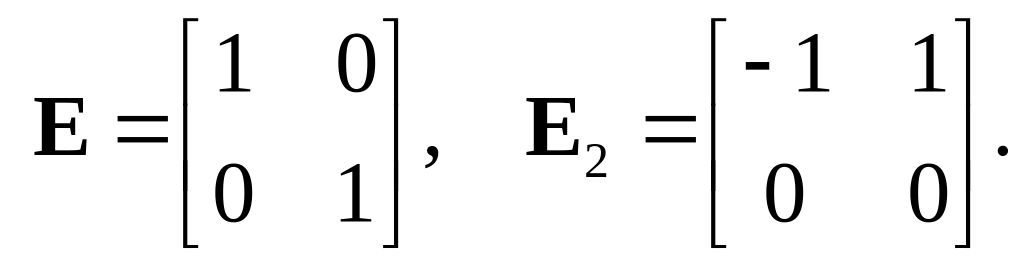
Собственные частоты линеаризованной системы при малых колебаниях около положения равновесия при соответственно равны и . Определим область устойчивости для системы (3.8) в предположении, что потенциальная сила и следящая сила постоянны. Характеристическое уравнение для (3.8) имеет вид

. (3.9)

Коэффициенты этого уравнения даются выражениями

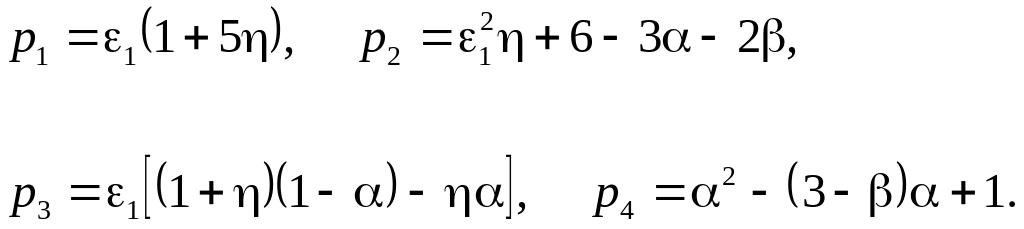(3.10)

Для устойчивости тривиального решения уравнений (3.8) необходимо и достаточно, чтобы все корни характеристического уравнения (3.9) имели отрицательные действительные части. Согласно модифицированному критерию Рауса–Гурвица для этого необходимо и достаточно выполнение неравенств

. (3.11)

Область устойчивости на плоскости , примыкающая к началу координат, ограничивается двумя кривыми и (рисунок 3.2). Одна из них (граница области дивергенции) соответствует нарушению третьего из неравенств (3.11). Ее уравнение определяется выражением , не зависящим от величины демпфирования в системе. Пересечение этой границы приводит к квазистатической потере устойчивости. Граница области флаттера определяется условием . Положение этой границы существенно зависит от отношения коэффициентов демпфирования . На рисунке 3.2 кривая построена для случая . При критическое значение параметра . При постоянном значении следящей силы, если , флаттер наступает при . Кривые и пересекаются при и . Граница области устойчивости строилась также и непосредственным вычислением корней характеристического уравнения. При этом определялась и частота флаттера (штриховая линия), как мнимая часть характеристического показателя, переходящего в правую полуплоскость при изменении параметров и .

В

С

Рисунок 3.2 Область устойчивости и частота флаттера для двойного маятника при постоянных во времени параметров нагрузки и

Рассмотрим теперь случай действия только периодической мертвой силы , положив . При этом мы имеем стандартную задачу об определении областей неустойчивости для гамильтоновой системы при периодическом параметрическом воздействии. Для решения этой задачи применим теорию Флоке - Ляпунова . Будем вычислять матрицу монодромии и определять ее собственные значения (мультипликаторы). Прямолинейная форма равновесия системы будет устойчивой, если все мультипликаторы по модулю меньше единицы, и неустойчивой, если модуль хотя бы одного мультипликатора превысит единицу. Численная реализация состояла в следующем. Уравнения (3.8) приводились к нормальной форме Коши. При заданных значениях параметров и и при начальных условиях, соответствующим столбцам единичной матрицы, четыре раза проводилось численное интегрирование в течение периода времени, равного . Искомым объектом при этом являлся матрицант, который в начале периода равен единичной матрице. Матрица монодромии есть значение матрицанта в конце периода времени . Далее вычислялись собственные значения матрицы монодромии . Границе областей неустойчивости соответствует условие .

На рисунке 3.3 на плоскости построены границы области неустойчивости при периодическом изменении мертвой силы. Как и следовало ожидать, главные параметрические резонансы наблюдаются на частотах и . Комбинационный резонанс суммарного типа имеет место в окрестности частоты . Траектории перемещения мультипликаторов для и представлены на рисунке 3.4, откуда видно, что на границе областей неустойчивости имеются периодические решения, так как мультипликаторы выходят за единичную окружность (штриховая линия) через значения , и почти периодические решения для комбинационного резонанса суммарного типа.

Рисунок 3.3 Области неустойчивости при периодическом изменении мертвой силы и

Рисунок 3.4 Траектории мультипликаторов для случая , , и изменении в диапазоне

Результаты вычислений для случая, когда следящая сила изменяется по закону при представлены на рисунке 3.5. Из-за несимметрии матрицы система является неканонической. Здесь, кроме главных параметрических резонансов и наблюдается параметрический резонанс разностного типа . Траектории мультипликаторов, построенные при и (рисунок 3.6), показывают, что на границах областей неустойчивости, кроме почти периодических решений в окрестности частоты , возможны только периодические решения, так как выхода мультипликаторов из единичной окружности через значение в данном случае не происходит. Аналогично ведет себя система и при одновременном синфазном изменении мертвой и следящей сил с одинаковой частотой: и . Области неустойчивости на плоскости для этого случая представлены на рисунке 3.7.

Рисунок 3.5 Области неустойчивости при периодическом изменении следящей силы и

Рисунок 3.6 Траектории мультипликаторов для случая , , и изменении в диапазоне

A

B

C

Рисунок 3.7 Области неустойчивости при синфазном периодическом изменении мертвой и следящей сил и

ВЫВОД

Целью данной работы является разработка алгоритмов и программ для исследования параметрических колебаний в различных механических системах при наличии неконсервативных сил. В качестве вычислительной системы и языка программирования предлагается использование системы Matlab и ее компоненты, реализующей цифровое имитационное моделирование Simulink. Необходимо было рассмотреть параметрические колебания таких систем, как двухзвенный маятник и консольный стержень при действии переменных по величине потенциальных и следящих сил. Для системы нужно было построить границы областей неустойчивости и провести многопараметрический анализ. Для двухзвенного маятника изучить динамическое поведение в областях параметрического резонанса.

Для исследования параметрической устойчивости использовали метод матриц монодромии, согласно алгоритму которого составлена программа вычислений и получены численные результаты для областей параметрического резонанса на плоскости коэффициент модуляции – частота параметрического воздействия.