Сурет - Канондық түрдегі рекурсивті сүзгінің құрылымдық сұлбасы

3.x(k)=0,1,0,1,0….

x(n) функциясының – нақты немесе комплексті санаулар тізбегінің тура Z-түрлендіруі деп келесі өрнекті айтады:

(1)

Біздің жағдай үшін:

Билет 13

1. Кері Z- түрлендіру

Отыскание оригинала, т. е. функции sД(t) или x(k), по заданному изображению Ŝ(Z) производится с помощью обратного Z-преобразования, получим

Интегрирование ведется по окружности радиуса , в которую преобразуется прямая σ=c из плоскости .Видно, что спектральные коэффициенты Ŝ(n), т. е. ДПФ последовательности {s(k)}, k=0, 1, …, N – 1}, равны значениям Z-преобразования этой последовательности в N точках, равномерно распределенных по единичной окружности.

См. дополнит. Лист

Функцияның оригиналын табу sД(t) немесеx(k) функциясының, берілген S(z) бейнесі арқылы кері Zтүрлендіру формуласы арқылы жүзеге асады

Интегралдау шеңбер радиусы бойынша жүзеге асады, бұл жерде тік σ=c жазықтығынан түрленеді.S(n)-нін спектральді тізбегі {s(k)}, k=0, 1, …, N – 1}, Z-түрленген тізбектегі N нүктесіндегілеріне тең екенін байқауға болады

2.Есеп

Кіріс санаулары {x()}={1,1,1,0,0…}; импульстік функциясы: {h(m)}={1,2,3,2,1}

y(0)=1·1=1; y(1)=1·2+1·1=3; y(2)=1·3+1·2+1·1=6

y(3)=1·2+1·3+1·2+1·0=7; y(4)=1·1+1·2+1·3+0·2+0·1=6; y(5)= 1·1+1·2+0·3+0·2=3

y(6)=1·1+0·2+0·3=1; y(7)=0·1+0·2=0; y(8)= 0·1=0

Шығыс санауларының мәні: {y(n)}={1,3,6,7,6,3,1,0,0}

Беріліс функциясы:

Билет 14

1.Тура Z-түрленуі. Сызықтық теоремасы.

Zтүрлендіруінің жалпы түсінігі х(nT) тізбегінің Z түрлендіруі деп келесі қатарды айтамыз мұндағы z{x(nT)} бұл z түрлендіруінің символды белгіленуі х(nT)-оригинал тізбек және бұл тізбек иөмендегі шартты қанағаттандыру керек х(nT)=0 x(z)-бұл х(nT)-тізбегінің Z аймақтағы Z бейнесі Z түрлендіруі.

Z түрлендіруінің негізгі қасиеті оның бір мәндәләгә яғни х(nT)- тізбегі оның Z бейнесі x(z) арқылы бір мәндәләкпен сол бейненің анықтау облысында анықталады. Өз кезегінде Z бейнеде x(t) тізбегімен бір мәндәләкпен анықталады.

Сызықтылық қасиеті егер х(nT) тізбегі басқа тізбектердің сызықты конбинациясына тең болса x(nT)=a1x1(nT)+a2x2(nT)+…, онда оның z бейнесі сол қолданылған тізбектердің z бейнелерінің сызықтық комбинациясына тең болады. z{x(nT)}=x(z)=a1x1(z)+a2x2(z)+…

2.Есеп

Дискретті үйірткі {y(n)}

1 .

{y(n)}={0,1,1,3,5,4,2,2,1}

2.Рекурсивті емес цифрлық сүзгілеудің беріліс функциясы

3.Цифрлық сүзгі таратуының жиіліктік коэффициенті

4) Рекурсивті сүзгінің құрылымдық сұлбасы

Билет 15

1.Тура Z-түрленуі.Кідірту теоремасы

Zтүрлендіруінің жалпы түсінігі х(nT) тізбегінің Z түрлендіруі деп келесі қатарды айтамыз мұндағы z{x(nT)} бұл z түрлендіруінің символды белгіленуі х(nT)-оригинал тізбек және бұл тізбек иөмендегі шартты қанағаттандыру керек х(nT)=0 x(z)-бұл х(nT)-тізбегінің Z аймақтағы Z бейнесі Z түрлендіруі.

Z түрлендіруінің негізгі қасиеті оның бір мәндәләгә яғни х(nT)- тізбегі оның Z бейнесі x(z) арқылы бір мәндәләкпен сол бейненің анықтау облысында анықталады. Өз кезегінде Z бейнеде x(t) тізбегімен бір мәндәләкпен анықталады.

Кідірілген тізбектің Z түрлендіруі х[(n-m)T] мынадай тізбек, m-санауға кешіккен тізбек Z бейнесі x(nT) тізбегін яғни ешқандай кідірмеген тізбектің Z бейнесін көбейткенге тең болады z{x(nT)}=x(z)=Z{х[(n-m)T]}=x(z)*

2.Есеп

Д искретті үйірткі {y(n)}

1. .

{y(n)}={1,2,2,4,4,4,5,4,1}

2. Рекурсивті емес цифрлық сүзгілеудің беріліс функциясы

3. Цифрлық сүзгі таратуының жиіліктік коэффициенті

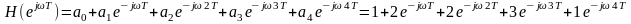
4 Рекурсивті сүзгінің құрылымдық сұлбасы

Билет 16

1.Тура Z-түрленуі. Уйірткі теоремасы

Zтүрлендіруінің жалпы түсінігі х(nT) тізбегінің Z түрлендіруі деп келесі қатарды айтамыз мұндағы z{x(nT)} бұл z түрлендіруінің символды белгіленуі х(nT)-оригинал тізбек және бұл тізбек иөмендегі шартты қанағаттандыру керек х(nT)=0 x(z)-бұл х(nT)-тізбегінің Z аймақтағы Z бейнесі Z түрлендіруі.

Z түрлендіруінің негізгі қасиеті оның бір мәндәләгә яғни х(nT)- тізбегі оның Z бейнесі x(z) арқылы бір мәндәләкпен сол бейненің анықтау облысында анықталады. Өз кезегінде Z бейнеде x(t) тізбегімен бір мәндәләкпен анықталады.

Тізбек үйірткісінің Z түрлендіруі x1(nT) x2(nT) осындай екі тізбек үйірткісі дегеніміз мынадай қарым-қатынаспен анықталатын өрнекті айтамыз

Осы тізбектірдің үйірткісінің Z бейнесі үйірткі процесіне қатысатын тізбектердің Z бейнелерінің көбейтіндісіне тең

Z{х[(n-m)T]}=x(z)=x1(z)*x2(z)

2.Есеп

д искретті уйірткі {y(n)}

1.

{y(n)}={1,2,4,5,6,5,3,1,1}

2. Рекурсивті емес цифрлық сүзгілеудің беріліс функциясы

3. Цифрлық сүзгі таратуының жиіліктік коэффициенті

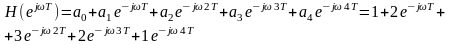
4 . Рекурсивті сүзгінің құрылымдық сұлбасы