Билет 1
1 СЦӨ құрылымдық сұлбасы. ТЖС, АЦТ және оларда болатын процесстердің тағайындалуы.
Ж
үйенің
кірісіне шектелген ұзақтықпен x(t)
аналогты сигналы келіп
түседі (физикалық сигнал – кернеу немесе
ток). Соңғы ұзақтық бойынша оның спектрі
шексіз болып келеді. Спектрдің шексіздігі
x(t) сигналын цифрлық күйге
түрлендіру үшін кедергі болады. ТЖС:
спектрді шектеу үшін қолданылады. Спектр
жоғарғы жиілік Fв-мен шектеледі, Найквист
жиілігі д/а(
).Fв
мәні сигнал түріне және есепке қатысты
анықталады. Мысалы, стандартты телефондық
сигналдың Fв=3,4 кГц-минималды стандартты
жиілігі, оның дискреттеу жиілігі fд=8
кГц. Спектрді Fв жиілігіне дейін шектеу
аналогты ТЖС(антиэлайсингті) арқылы
жүзеге асады. АЦП: x(t) сигналы АЦП-ның
кірісіне келіп түседі, бұнда сигналдың
уақыт бойынша дискреттелуі және деңгей
бойынша квантталуы жүзеге асады.
Дискреттеу кезінде x(t) аналогты сигналы
уақыт аралығы бойынша алынған лездік
мәндерінің санауларына x(nT) ауысады.
Дикреттеу интервалы Т кішірек болса,
x(nT) санаулар тізбегі бастапқы сигналды
дәлірек бейнелейтін болады. Дискреттеу
интервалын дискреттеу жиілігімен
анықтайды T=1/fд. Fд жоғары болған
сайын,санауларға операциялар орындау
қиындай түседі және оның құрылғысы да
күрделенеді.
2.Есеп
Құрылымдық сұлба
Беріліс сипаттамасы: Н(z)
{x(k)}=1,1,0,0,0
Н(
=
Н(
=
Н(
*
Н(
=(1+
)*
=
x(z)=1
+1
=1+
Шығыс сигналы:Y(z)
Y(z)=H(z)*X(z)=
=
Билет 2
1. СЦӨ құрылымдық сұлбасы. АЦТ, есептеуіш құрылғылар және оларда болатын процесстердің тағайындалуы.
АЦП: x(t) сигналы АЦП-ның кірісіне келіп түседі, бұнда сигналдың уақыт бойынша дискреттелуі және деңгей бойынша квантталуы жүзеге асады. Дискреттеу кезінде x(t) аналогты сигналы уақыт аралығы бойынша алынған лездік мәндерінің санауларына x(nT) ауысады. Дикреттеу интервалы Т кішірек болса, x(nT) санаулар тізбегі бастапқы сигналды дәлірек бейнелейтін болады. Дискреттеу интервалын дискреттеу жиілігімен анықтайды T=1/fд. Fд жоғары болған сайын,санауларға операциялар орындау қиындай түседі және оның құрылғысы да күрделенеді.
Есептеуіш құрылғылар: fд жоғары болған сайын, есептеуішке санаулар келіп түскен темпте, соған сай көбірек операциялар орындау қиынға түседі,ғ жіне құрылғы да күрделі болуы тиіс. Яғни, сигналдың дәлдігі fд жиілігін ұлғайтуға, ал, құрылғыны қарапайым ету үшін жиілікті төмендетуге алып келеді. Алайда fд мәнінің минималды шектеуі бар: үзіліссіз x(t) сигналын x(nT) санаулары арқылы толығымен қайта қалпына келтіру үшін fд дискреттеу жиілігі Fв жиілігінен екі есеге үлкен болуы қажет және жеткілікті. fд>=2Fв (Котельников теоремасы).
2.Есеп
Екі тізбектей қосылған : 1-ретті рекурсивті емес және 2- ретті рекурсивті сүзгілерден тұратын цифрлық сүзгінің құрылымдық сұлбасы
Беріліс
сипаттамасы
для послед. Соед.
Егер кіріс сигналдары {x(k)} есеп берулерімен көрсетілсе , онда шығыс сигналдың Z-түрлендіруін анықтаңдар.
x(k)}={0,1,1,0,0…}
Билет 3
1. СЦӨнің құрылымдық сұлбасы, ЦАТ, процессор және онда болатын процесстердің тағайындалуы.
Процессордың
тағайындалуы: дискретизация жиілігі
көп болған сайын есептеуіштің құрылымдық
сұлбасы үлкен әрі секундқа келіп түсетін
операциялар саны ұлғаяды. Ол дегеніміз
сигналдың дәлділігі дисктеризация
жиілігін көбейтуді талап етеді, ал
құрылымдық сұлбасын кішірейту
дискретизация жиілігін азайтуға алып
келеді. Дискретизация жиілігінің ең
кіші мәніне шектеу бар ол дегеніміз
сигналдың дискреттеу жиілігі үздіксіз
сигналдың спектінің ең улкен мәнінен
екі есе улкен болуы қажет. Жиілікті
шектеу ТЖС пен жүзеге асады. ЦАТ қойылатын
шарттардың ішінде оның такті жиілігі
дискретизация жиілігінен жүз есе жоғары
болуы қажет. ЦАТ келіп түскен мәндердерден
баспалдақты сигналды шығарып береді
2.Есеп
Беріліс
теңдеуі
тізбектей қосылу үшін.
Z-түрлендіруді
анықтау {x(k)}
x(k)}={1,1,0,0,0…}
Билет 4
1 СЦӨ құрылымдық сұлбасы. ЦАТ, түзеткіш сүзгі және оларда болатын процесстердің тағайындалуы.
ЦАП: Алынған шығыс санаулары ЦАП құрылғысына түседі, әғни бұл жерде баспалдақты сигналды формаланады у(t). ТЖС: Спектрді Fв жиілігіне дейін шектеу аналогты ТЖС(антиэлайсингті) арқылы жүзеге асады.
2 Есеп
X(k) = 1,0,1,0,0…
Билет 5
1. Сигналдардың негізгі түрлері: Сигналдардың аннықтамалары және математикалық сипаттамалары
Сигнал – бұл құрамында өзіндік хабары
бар физикалық процесс. Іс жүзінде
көбінесе электрлік сигналдар қолданылады.
Сонын өзінде, электрлік тізбекте хабар
таратушы ретінде, уақыт бойынша өзгеретін
ток және кернеу болып табылады. Электрлік
сигналдарды басқа сигналдарға қарағанда
өңдеу оңайға түседі, олар үлкен қашықтыққа
жақсы беріледі.
Сигналдардың үш түрі бар: аналогты, дискретті және цифрлық сигналдар.
Аналогты
сигналдар (АС). Көбінесе сигналдардың
табиғаты аналогты болып келеді, бұл
дегеніміз олар ууақыт бойынша үзіліссіз
өзгере отырып, белгілі интервалда кез
келген мәнге ие бола алады. Аналогты
сигналдар уақыттық
математикалық
функциясымен сипатталады. Мысалы АС –
гармоникалық сигнал:
немесе экспоненциалды –
сигнал. Аналогты сигнал телефонияда,
радиохабарда, теледидарда қолданылады.
Мұндай сигналды компьютерге енгізіп,
өңдеуге мүмкін емес, өйткені уақыттың
кез келген интервалында ол шексіз көп
мәнге ие болады, ал оның нақты мәндерін
(қателіксіз) алу үшін шексіз разрядты
сандар қажет. Сондықтан аналогты сигналды
берілген разрядты сандарының тізбегі
арқылы көрсету үшін, түрлендіру қажет.
Дискретті
сигнал. Аналогты сигналының дискреттелуі
дегеніміз – уақыттың
дискретті
моменттерінде алынған сигналдардың
тізбекті мәндер күйінде берілуін
айтамыз. . Бұл мәндер санаулар
деп аталып, ал
-
дискреттелу интервалы делінеді.
Санаулардың соңғы
тізбегінің күйі:
.
Мысалы:
.Мұнда
:
;
;
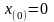2. Есеп
{x(k)}=1,0,0,1,0
рекурсивті фильтр- тура түрлену
Беріліс
теңдеуі
тізбектей қосылу үшін.
Z-түрлендіруді анықтау x(k)}={1,0,0,1,0…}
Билет 6
1. Аналогты сигналдар үшін тура Фурье түрлендіруі. Аналогты периодты сигналдардың спектрі және жалғыз аналогты импульстің спектрі.
Аналогты және дискретті сигналдарды жиіліктік аймақта сипаттау үшін Фурье түрлендіру аппаратын қолданады. х(t) аналогты сигналдың Х(ϳω) спектрін Тура Фурье түрлендіруі деп атайды.
Х(ϳω)- комплексті спектрлік
тығыздығы
Сол
сияқты х(t) сигналын өзінің спектрі
арқылы да қалпына келтіруге болады
(кері Фурье түрлендіруі).
Егер х(t) сигналы өзінің ұзақтылығына тең Тс периодымен периодты сигнал болса, оның спектрі дискретті болады.
Х(ϳf)
орныны Х(ϳnF) санауларын қолдансақ, Ғ
жиілігі бойынша спектрді дискреттеу
интервалы сигнал периодымен анықталады.
Периодты
сигнал спектрі Х(ϳnF) :
Х(ϳnF)- n-ді гармоника комплексті амплитуда.
-
Фурье қатарының комплексті көрінісі.
Дискретті сигналға арналған Фурьенің тура және кері түрлендірулері:
және
Д
искретті
түрлендіру сызықтық
қасиетке ие: Дискретті сигнал қосындысына
олардың Дискретті Фурье Түрлендіу
қосындысы сәйкес келеді.
Аналогты периодты сигналдардырң спектрі мен жалғыз аналогты импульстің спектрі арасындағы байланыс:
2. Есеп
X(k) = 0,1,0,1,0…
Билет 7
1. Дискреттелген сигналдың есеп берулерін дельта-функция, спектрлік тығыздық түрінде көрсетілуі
Телекоммуникациялық жүйеде ең алғашқы типтік сигналдың мысалы ретінде дельта-функция немесе Дирак функциясы деп аталатын типтік сигнал қарастырылады.
Дельта функция дегеніміз шексіз амплитудасы бар және шексіз жіңішке көрініске ие болатын аргументтің нөлдік мәнінде орналасатын функцияны айтамыз. Дельта функцияның негізгі параметрі немесе өлшемі шексіздік жағдайында тұрса да, оның ауданы 1-ге тең деп есептелінеді
,
Бұл
дельта функцияның телекоммуникацияға
қажетті бір қасиеті: сүзгілеу қасиеті
Аналогты
сигналдың дельта функция түрінде
берілуі:
Осы
сигналдың дискреттелген түрдегі дельта
функциясы мынандай болады:
n=0,1,2,3…
Бастапқы аналогты сигналдардың спектральды тығыздығын табатын формула:
Бастапқы берілген сигналды сол сигналдың спектрі арқылы қалпына келтіру:
Дискретті
сигналдар үшін Фурье түрлендіруі
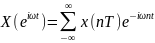
Билет 8
1.Жалғыз импульстің спектральді тығыздығы мен жалғыз дискреттелген импульстің спектральді тығыздығы арасындағы байланыс
Жалғыз импульстік функция (1):
n=0,±1,±2,±3,…
Дискретті жалғыз секіріс (2):
n=0,±1,±2,±3,…
Дискретті экспоненциалды функция (3):
n=0,±1,±2,±3,…
|а|<1 болса, экспонента кемуші, ал |а|>1 – өсуші. а<0 – айнымалы, ал а=1 кезінде санаудың барлық мәндері бірдей және 1-ге тең, n≥0.
Дискретті өшуші синусоида (4):
n=0,±1,±2,±3,…; Т –дискретизация период; А – амплитуда, ω – бұрыштық жиілік
2.Есеп
a0 =2, a1=1, a2= 3, a3=2, a4=4, a5= 5
b1=1, b2= 2, b3=4, b4=3, b5= 5
x(k) = 1,1,1,0,0,…
1)
2) Канондық түрдегі рекурсивті сүзгі
3)
Билет 9