3.1.3 Вывод

Вычислим допустимое для смешанных СМО значение времени пребывания заявки в системе

Вычислив показатели эффективности для СМО с отказами, учитывая число каналов обслуживания равное от единицы до шести, мы выяснили, что СМО с отказами при использовании шести каналов обслуживания является наилучшей т.к. минимальная стоимость обслуживания одной заявки в единицу времени (С) в этом случае является наименьшей. Из этого следует, что система с шестью каналами обслуживания(n=6) является оптимальной.

3.2 Смешенная система массового обслуживания с ограничением на длину очереди

3.2.1 Задачи этапа

Изучается одна из смешанных систем, соответствующая заданию на курсовое проектирование. Определяется наименьшее значение С – средней стоимости обслуживания одной заявки в единицу времени.

На этом этапе решается вопрос о возможности с введением очереди обеспечить уменьшение значения оптимального для рассматриваемой системы значения экономического показателя С и улучшить другие показатели эффективности изучаемой системы.

СМО с ограничением на длину очереди.

В рассматриваемом случае анализируется влияние на эффективность системы ограничения на длину очереди. Длина очереди не должна превышать заданной величины m.

Исходные данные изучаемой системы:

• λ – интенсивность входного потока,

• – среднее время обслуживания одной заявки для рассматриваемого варианта системы.

• n = – число каналов обслуживания рассматриваемой смешенной системы должно совпадать с найденным ранее числом каналов оптимальной системы с отказами.

• m –допустимая длина очереди.

_{Задаваясь рядом значений параметра, m вычисляются зависимости} . Оптимальной считается система, имеющая наименьший показатель эффективности С. В том случае, когда зависимость имеет монотонный характер, наилучшим значением показателя является наименьшее значение C, при котором ещё выполняется условие

3.2.2 Расчетная часть

1)Расчет показателей эффективности для СМО с ограничением на длину очереди при m=1:

=0.237;

=0.231;

=0.128;

=0,128

= 0,872;

3,487;

= 0,513;

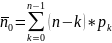=1,386;

= 5,615;

0,936;

=1,436;

3,000;

0,860.

Таблица 2.3- Результаты вычислений эффективности СМО с ограничением на длину очереди

Система с ограничениями на длину очереди							Результирующие
							показатели
m				1 /ед.вр.	1/ед.вр.	Cобщ ед.ст		C			е д.вр
								ед.ст
	Данные системы с отказами
m = 0	4,410	1,590	0	1,060	2,940	2,735		0,930	0,735	0,735	1,103
Данные системы c ограничением на длину очереди
1	5,615	1,386	0,128	0,513	3,487	3,000		0,860	0,872	0,936	1,436
2	5,143	3,086	0,857	1,143	2,857	3,057		1,070	0,714	0,857	1,500
3	5,333	2,400	1,333	0,889	3,111	3,111		1,000	0,778	0,889	1,667
4	5,455	1,964	1,818	0,727	3,273	3,164		0,967	0,818	0,909	1,818
5	5,538	1,662	2,308	0,615	3,385	3,215		0,950	0,846	0,923	1,962
6	5,600	1,440	2,800	0,533	3,467	3,267		0,942	0,867	0,933	2,100

Таблица 2.4- Результаты вычислений общей стоимости обслуживания заявок в единицу времени для СМО с огриничением на длину очереди

К вычислению общей стоимости обслуживания заявок в единицу времени
m	ед.стоим.	ед.стоим.	ед.стоим.	ед.стоим.	Cобщ
					ед.стоим.
Данные системы с отказами
m = 0	2.205	0.318	0	0.212	2.735
Данные системы ограничениями на длину очереди
1	2,808	0,077	0,013	0,103	3,000
2	2,571	0,171	0,086	0,229	3,057
3	2,667	0,133	0,133	0,178	3,111
4	2,727	0,109	0,182	0,145	3,164
5	2,769	0,092	0,231	0,123	3,215
6	2,800	0,080	0,280	0,107	3,267

Зависимость средней стоимости обслуживания одной заявки в единицу времени (C) от ограничения на длины очереди(m) показана на Графике 3.5.

График 3.5 – График зависимости средней стоимости обслуживания одной заявки в единицу времени (C) от ограничения на длину очереди(m)

Зависимость вероятности обслуживания заявки (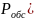 от ограничения на длину очереди (m) показана на Графике 3.6.

График 3.6 - График зависимости вероятности обслуживания заявки ( от ограничения на длину очереди (m)

Зависимость коэффициента загрузки системы ( от ограничения на длину очереди (m) показана на Графике 3.7.

График 3.7 – График зависимости коэффициента загрузки системы ( от ограничения на длину очереди (m)

Зависимость времени пребывания заявки в системе ( от ограничения на длину очереди показана(m) на Графике 3.8.

График 3.8 - График зависимости времени пребывания заявки в системе ( от ограничения на длину очереди(m)