1.3 Компетенции, реализуемые при изучении дисциплины
Код компетенции |
Компетенции |
общекультурные компетенции, введенные Образовательным стандартом НИЯУ МИФИ |
|
ОСК-1 |
способность использовать основные законы естественнонаучных дисциплин в профессиональной деятельности, применять методы математического анализа и моделирования, теоретического и экспериментального исследования |
Навыки, полученные в данной дисциплине, помогают в изучении дисциплин, формирующих компетенцию ОПК-1 «Способность использовать основные закономерности, действующие в процессе изготовления машиностроительных изделий требуемого качества, заданного количества при наименьших затратах общественного труда» и ПК-3 «Способность участвовать в постановке целей проекта (программы), его задач при заданных критериях, целевых функциях, ограничениях, разработке структуры их взаимосвязей, определении приоритетов решения».
2 Контрольная работа
В КАЖДОМ ВАРИАНТЕ
№1 –4 балла, №2 – 2 балла, №3: 1–2 б., 2– 1 б., 3–2 б., 4 –2б., 5 – 16 б.
Вариант №1
№1 Вычислить пределы
1)
при а1=0,
а2=1,
а3=
-1, а4=
;
2)
;
3)
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №2
№1 Вычислить пределы
1)
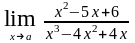при а1=0,
а2=2,
а3=
-1, а4=
;
2)
;
3)
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №3
№1 Вычислить пределы
1)
при а1=0,
а2=1,
а3=
-1, а4=
;
2)
;
3)
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №4
№1 Вычислить пределы
1)
при а1=0,
а2=1,
а3=
-1, а4=
;
2)
;
3)
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
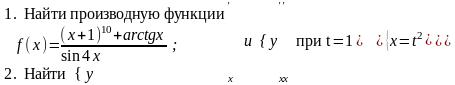
Вариант №5
№1 Вычислить пределы
1)
при а1=0,
а2=1,
а3=
-1, а4=
;
2)
;
3)
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №6
№1 Вычислить пределы
1)
при а1=0,
а2=2,
а3=
-1, а4=
;
2)
;
3)
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №7
№1 Вычислить пределы
1)
;
2)
;
3)
при а1=0,
а2=2,
а3=
-1, а4=
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №8
№1 Вычислить пределы
1)
;
2)
при а1=0,
а2=1,
а3=
-1, а4=
;
3)
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №9
№1 Вычислить пределы
1)
;
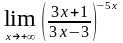2)
;
3)
при а1=0,
а2=1,
а3=
-1, а4=
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №10
№1 Вычислить пределы
1)
при а1=0,
а2=2,
а3=
-1, а4=
;
2) ;
3)
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №11
№1 Вычислить пределы
1)
;
2)
при а1=0,
а2=1,
а3=
-1, а4=
;
3)
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №12
№1 Вычислить пределы
1)
при а1=0,
а2=2,
а3=
-1, а4=
;
2)
;
3)
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №13
№1 Вычислить пределы
1)
;
2)
при а1=0,
а2=1,
а3=
-1, а4=
;
3)
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №14
№1 Вычислить пределы
1) при а1=0, а2=2, а3= -1, а4= ;
2) ;
3)
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №15
№1 Вычислить пределы
1)
;
2)
;
3)
при а1=0,
а2=2,
а3=
-1, а4=
+
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №16
№1 Вычислить пределы
1)
;
2)
при а1=
-2, а2=2,
а3=
-1, а4=
;
3)
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №17
№1 Вычислить пределы
1)
;
2)
при а1=0,
а2=1,
а3=
-1, а4=
;
3)
.
№2 Найти область определения функции у=f(x),
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №18
№1 Вычислить пределы
1) при а1=0, а2=2, а3= -1, а4= ;
2) ;
3)
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов.
№3
Вариант №19
№1 Вычислить пределы
1)
;
2)
при а1=0,
а2=1,
а3=
-1, а4=
;
2)
;
3).
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №20
№1 Вычислить пределы
1) ;;
2)
;
3)
при а1=0,
а2=1,
а3=
-1, а4=
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №21
№1 Вычислить пределы
1) ;
2) ;
3)
при а1=0,
а2=3,
а3=
-1, а4=
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №22
№1 Вычислить пределы
1) при а1=0, а2=2, а3= -1, а4= ;
2)
;
3)
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №23
№1 Вычислить пределы
1) ;
2)
;
3)
при а1=0,
а2=-2,
а3=
-1, а4=
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №24
№1 Вычислить пределы
1)
;
2) при а1=0, а2=1, а3= -1, а4= ;
3)
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №25
№1 Вычислить пределы
1)
;
2)
;
3)
при а1=0,
а2=1,
а3=
-1, а4=
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №26
№1 Вычислить пределы
1)
2) при а1=0, а2=2, а3= -1, а4= ;
3) .
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №27
№1 Вычислить пределы
1)
;
2)
при а1=0,
а2=1,
а3=
-1, а4=
;
3)
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №28
№1 Вычислить пределы
1)
;
2)
;
3)
при а1=0,
а2=2,
а3=
-1, а4=
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №29
№1 Вычислить пределы
1) ;
2)
при а1=6,
а2=1,
а3=
-1, а4=
;
3)
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
Вариант №30
№1 Вычислить пределы
1)
при а1=0,
а2=2,
а3=
-1, а4=
;
2)
;
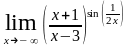3)
.
№2 Найти область определения функции у=f(x),
,
построить её
график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
2.