33. Закон полного тока для магнитного поля в вакууме(теорема о циркуляции вектора в).

циркуляция вектора напряженности электростатического поля вдоль замкнутого контура равна нулю, откуда следует потенциальный характер электростатического поля. Одним из основных отличий магнитного поля от электростатического поля является его непотенциальность. Для доказательства этого рассмотрим линейный интеграл    от В по замкнутому пути в магнитном поле, создаваемом током, т.е.

где  – вектор элемента длины контура, направленный вдоль обхода контура; В_ℓ – проекция  вектора   на направление касательной к контуру. Данный интеграл называется циркуляцией вектора   по заданному замкнутому контуру ℓ. 

34. Магнитный момент атома- электрон в атоме движется по круговой орбите и, следовательно, имеет механический момент и создает круговой ток, порождающий магнитный момент.

Теорема Лармора- под действием внешнего магнитного поля происходит прецессия орбиты электрона и вектора магнитного момента с угловой скоростью вокруг оси, проходящей через ядро атома и параллельной вектору.

.

молекулярный ток: макротоками называются токи проводимости и конвекционные токи, связанные с движением заряженных макроскопических тел.

Микротоками называют токи, обусловленные движением электронов в атомах, молекулах и ионах.

47. Дефференциальное уравнение затухающих электромагнитных колебаний в контуре.

d²q/dt² + 2βdq/dt + ω₀²q = 0

Характеристики:

1. Коэффициент затухания β.

2. Логарифмический декремент затухания δ - физическая величина, численно равная натуральному логарифму отношения двух последовательных амплитуд, отстоящих по времени на период .

3. Добротность Q колебательной системы – безразмерная физическая величина, равная произведению величины (2π) νа отношение энергии W(t) системы в произвольный момент времени к убыли энергии за один период затухающих колебаний:

.

Так как энергия пропорциональна квадрату амплитуды, то

.

При малых значениях логарифмического декремента δ добротность колебательной системы равна

,

где N_e – число колебаний, за которое амплитуда уменьшается в "е" раз.

4. При увеличении коэффициента β, частота затухающих колебаний уменьшает-ся, а период увеличивается. При ω₀ = β частота затухающих колебаний становится равной нулю ω_зат. = 0, а Т_зат. = ∞. При этом колебания теряют периодический характер и называются апериодическими.

При ω₀ = β параметры системы, ответственные за убывание колебательной энергии, принимают значения, называемые критическими. Для пружинного маятника условие ω₀ = β запишется так: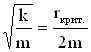 , откуда найдем величину критического коэффициента сопротивления:

.

Для LCR – контура условие  позволяет вычислить критическое сопротивление контура, при котором колебания потеряют свою периодичность:

.

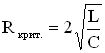48. Дефференциальное уравнение вынужденных электромагнитных колебаний в контуре.Резонанс.

В электронных устройствах резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.  Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.