Вопрос 45.Колебательный процесс в контуре. Превращение энергии

Колебательный контур - это устройство, предназначенное для генерации (создания) электромагнитных колебаний.

Колебательный контур состоит из катушки и конденсатора. Кроме того, в нём также может присутствовать резистор (элемент с переменным сопротивлением). Катушка индуктивности (или соленоид, как её иногда называют) представляет собой стержень, на который наматываются несколько слоёв обмотки, которая, как правило, представляет собой медную проволоку. Именно этот элемент создаёт колебания в колебательном контуре. Стержень, находящийся в середине, часто называют дросселем, или сердечником, а катушку иногда именуют соленоидом.

Чтобы возбудить колебания в этом контуре, необходимо сообщить конденсатору некоторый заряд от источника ε. Когда ключ K находится в положении 1, конденсатор заряжается до напряжения . После переключения ключа в положение 2 начинается процесс разрядки конденсатора через резистор R и катушку индуктивности L. При определенных условиях этот процесс может иметь колебательный характер

При замыкании на катушку предварительно заряженного конденсатора С в колебательном контуре возникают свободные колебания заряда конденсатора и тока в катушке.

Правило Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им переменное магнитное поле препятствует изменению магнитного потока, вызвавшему этот индукционный ток. Когда конденсатор С разрядился, а следовательно, энергия магнитного поля и ток в цепи максимальные, то в этот момент ток I начинает убывать. Следовательно, магнитное поле в катушке ослабевает, и в катушке возникает индукционный ток Ii, который препятствует уменьшению магнитного поля. Направление Ii совпадает с направлением первоначального тока, и положительные заряды продолжают идти в том же направлении, заряжая положительно другую обкладку конденсатора С

ПРЕВРАЩЕНИЯ ЭНЕРГИИ В КОЛЕБАТЕЛЬНОМ КОНТУРЕПри отсутствии в колебательном контуре источника э. д. с. после зарядки конденсатора

(рис. 2, ключ К в положении 1) и замыкания цепи (ключ К в положении 2) в контуре возникают свободные электромагнитные колебания. Характер колебательных процессов (периодический, затухающий, апериодический) определяется соотношением параметров контураR ,L ,C .

Пусть в начальный момент времени t = 0 конденсатор заряжен, цепь разомкнута, и ток в контуре отсутствует. Энергия заряженного конденсатора при разности потенциалов на его

обкладках U C равна W =СUC2 . Э 2

Вопрос 46.Дифференциальное уравнение незатухающих электромагнитных колебаний в контуре. Характеристики.

Незатухающие колебания возникают в колебательном контуре, в котором имеется катушка индуктивности L и конденсатор C, активное сопротивление R=0.

В таком контуре происходит перекачка энергии конденсатора (электрическая энергия) в энергию токов катушки (магнитная, аналог кинетической) и обратно.

В момент времени 

Конденсатор полностью заряжен.

.

В момент времени 

Конденсатор разряжается и в контуре потечет ток, поэтому возникает магнитное поле в катушке индуктивности и к моменту времени 

–max

В момент времени 

Ток начинает уменьшаться и по правилу Ленца в катушке будет индуцироваться ток того же направления, что и ток разряда конденсатора. Конденсатор начинает перезаряжаться.

–max

В момент времени 

Выведем дифференциальное уравнение свободных гармонических колебаний в контуре.

Возьмем производную по времени:

  37.Напряженностью магнитного поля называют векторную величину   , характеризующую магнитное поле и определяемую следующим образом:

,

  Напряженность магнитного поля заряда q, движущегося в вакууме равна:

,

в системе СИ — в амперах на метр (А/м) .1 А/м = 4π/1000 Э ≈ 0,01256637 Э.

38. Классификация магнитиков.По реакции на внешнее магнитное поле и характеру внутреннего магнитного упорядочения все вещества в природе можно подразделить на пять групп: диамагнетики, парамагнетики, ферромагнетики, антиферромагнетики и ферримагнетики. Перечисленным видам магнетиков соответствуют 5различных видов магнитного состояния вещества: диа-, пара-, ферро-, антиферро- и ферримагнетизм.

К диамагнетикам относят в-ва , у которых магнитная восприимчивость отрицательна и не зависит от напряженности внешнего магнитного поля. К диа- от-ся инертные газы, водород, азот, многие жидкости (вода, нефть и ее производные), ряд металлов (медь, серебро, золото, цинк, ртуть, галлий и др.), большинство полупроводников (кремний, германий, соединения АЗВ5, А2В6) и органических соединений, щелочно-галоидные кристаллы, неорганические стекла и др. Диамагнетиками являются все вещества с ковалентной химической связью и вещества в сверхпроводящем состоянии.

К пара- от-ят в-ва с положительной магнитной восприимчивостью, не зависящей от напряженности внешнего магнитного поля. К числу пара- от-ят кислород, окись азота, щелочные и щелочноземельные металлы, некоторые переходные металлы, соли железа, кобальта, никеля и редкоземельных элементов.

К ферро-относят вещества с большой положительной магнитной восприимчивостью (до 106), которая сильно зависит от напряженности магнитного поля и температуры.

14.Энергия системы заряженных проводников. Потенциал проводника, находящегося в электрическом поле, созданным другими проводниками, зависит не только от величины собственного заряда, но и от зарядов на других проводниках.

Энергия заряженного конденсатора. Конденсатор по определению представляет собой систему, состоящую из двух проводников с одинаковыми по величине и противоположными по знаку зарядами Q и Q , а также потенциалами 1 и 2 .

W-энергия; -потенциал;U-разность потенциалов

Объемная плотность энергии- ϶ᴛᴏ количество энергии, заключенное в единице объема. Объемная плотность энергии складывается из объемных плотностей энергии электрического и магнитного полей.

15.Электрический ток- упорядоченное движение заряженных частиц. Ток бывает постоянный и переменный. Постоянный ток — это ток, имеющий постоянную величину. Переменный ток периодически изменяет направление своего движения по синусоиде с определенной частотой.

Плотность тока - это количество заряда, прошедшего через единичную площадь в единицу времени, то есть - отношение силы тока к площади поперечного сечения проводника, по которому течёт ток. Является векторной величиной. Модуль плотности тока равен где j - модуль вектора плотности тока, I - сила тока, S - площадь поперечного сечения проводника.

Природа носителей тока. Носителями тока могут быть электроны, ионы, заряженные частицы.

Классическая теория электронной проводимости. Исходя из представлений о свободных электронах как основных носителях тока в металлах, Друде разработал классическую теорию электропровод-ности металлов, которая затем была усовершенствована Лоренцем.

Основные положения  этой теории сводятся к следующим:

1) Носителями тока в металлах являются электроны, движение которых подчиняется законом классической механики.

2) Поведение электронов подобно поведению молекул идеального газа (электронный газ).

3) При движении электронов в кристаллической решетке можно не учитывать столкновения электронов друг с другом.

4) При упругом столкновении электронов с ионами электроны полностью передают им накопленную в электрическом поле энергию.

12Напряженность электрического поля в диэлектриках.Поместим пластину однородного диэлектрика в электрическое поле   меж­ду двумя бесконечными парал­лельными разноименно заряженными плоскостями .Под действием внешнего поля диэлектрик поля­ризуется, в результате чего, на боковой грани диэлектрика, обращенной к положительной плоскости, появляется избы­ток отрицательных зарядов с поверхностной плотностью -s¢, а на противопо­ложной - избыток положительных заря­дов с поверхностной плотностью +s¢. Эти не скомпенсиро­ванные заряды называются связанными и они создают свое собст­венное добавочное поле   , направленное против внешнего поля    . Поэтому результирующая напряженность поля   в диэлектрике меньше   на величину   : 

Напряженность добавочного поля диэлектрика   можно определить с помо­щью формулы для напряженно­сти поля между параллельными бесконечными заря­жен­ными плоскостями:   . Определим поверхностную плотность связанных зарядов s¢. Для однородного диэлектрика, занимающего объем V, полный дипольный момент равен   , где S ‑ площадь боковой грани пластины, d - ее толщина. С другой стороны,   , где   ‑ связанный заряд боковой грани. Поскольку   , то   

13.

Влияние диэлектриков на электрическое поле сводится к ответному действию возникающих в поле поляризационных зарядов. Поэтому теорему Остроградского - Гаусса для тел в вакууме можно трансформировать, добавив к свободным зарядам поляризационные заряды и получить теорему с диэлектриками. В таком случае теорема Остроградского - Гаусса примет вид в системе СИ: ФE=∮SE→dS→=1ε0(∑i=1Nqi+∑j=1Kqjsv)

где q_jsv -- связанные заряды, q_i -- свободные заряды, Ф_е -- поток вектора напряженности электрического поля. Использование вектора электрического смещения (D→) существенно облегчает анализ поля при наличии диэлектрика. Так, например, теорема Остроградского -- Гаусса в интегральном виде при наличии диэлектрика может быть записана как: ∮SD→⋅dS→=∑i=1Nqi=Q

Поток вектора D→ через замкнутую поверхность определен только свободными зарядами. В вакууме векторы D→ и E→ совпадают.

Div D=p

где ρ -- объемная плотность свободных зарядов. Теорема Остроградского - Гаусса в виде и справедлива не только в электростатике, она выполняется и для переменных полей. Данная теорема является составной частью системы уравнений Максвелла.

49. Дифференциальное уравнение электромагнитной волны имеет вид: и

Решением этих волновых уравнений являются функции:

и

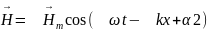
Основные свойства электромагнитных волн:

1 . Скорость распространения в непроводящей нейтральной неферромагнитной среде

2. Векторы 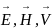(скорость волны) взаимно перпендикулярны и образуют правовинтовую систему.

Следовательно, вектор совпадает по направлению с векторным произведением

3 . Электромагнитные волны – поперечные волны, E и H лежат в плоскостях перпендикулярных направлению распространения волны.

4. В электромагнитной волне и колеблются в одинаковых фазах,

причем между мгновенными значениями

E и H в любой точке существует

cвязь .

Значения E и H одновременно достигают максимума, одновременно

обращаются в нуль.

50. Объемная плотность энергии электромагнитного поля w равна сумме

объемных плотностей энергии электрического и магнитного полей.

, - диэлектрическая и магнитная проницаемость среды.

Вектор Умова-Пойтинга.

Вектор плотности потока энергии электромагнитной волны называ-

ется вектором Умова-Пойнинга.

.

так как w=EH/ V , то получим: , где скорость переноса энергии или фазовая скорость волны.