1.Электрический заряд это физическая величина ,характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия. Обозначается q илиQ. Существует два рода электрических зарядов ,условно названных положительными и отрицательными. Заряды могут передаваться от одного тела к другому, одно и тоже тело в разных условиях может иметь разный заряд. Одноименные заряды отталкиваются ,разноименные притягиваются.

Закон сохранения электрического заряда утверждает ,что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака.

*

Точечным зарядом называют заряженность тело.размерами которого в условиях данной задачи можно пренебречь силы взаимодействия неподвижных зарядов прямо пропорциональны квадрату расстояния между ними. F=k |q1|×|q2|/r2. после k черточка и наверху q1иq2 будут.

4. Теорема Остроградского – Гаусса (теорема Гаусса): поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на :

– поток вектора напряженности электрического поля(Φ). Понятие потока вектора аналогично понятию потока вектора скорости при течении несжимаемой жидкости. Фактически поток вектора пропорционален числу линий напряженности, пронизывающих элементарную площадку ΔS (рис. 1.6).

Пусть в пространстве, где создано электрическое поле, расположена некоторая достаточно малая площадка ΔS. Произведение модуля вектора на площадь ΔS и на косинус угла α между вектором и нормалью к площадке называется элементарным потоком вектора напряженности через площадку ΔS:

,

где – проекция вектора на нормаль к площадке ; - единичный вектор, перпендикулярный площадке .

Рис. 1.6. К определению элементарного потока ΔΦ

Полный поток вектора напряженности сквозь поверхность в общем случае равен:

где . (Выбор нормали условен, но в случае замкнутых поверхностей принято брать наружу области, охватываемой этими поверхностями, т. е. выбирать внешнюю нормаль). Единица измерения потока - В·м.

5. Применение теоремы Гаусса к расчету электрических полей Использование теоремы Гаусса для расчета полей эффективно в тех случаях, когда поле обладает специальной симметрией (чаще всего плоской, цилиндрической или сферической). Симметрия и конфигурация поля должны быть такими, чтобы, во-первых, заряженное тело можно было бы окружить достаточно простой замкну- той поверхностью и, во-вторых, вычисление потока вектора напряженности свести к простому умножению Е (или En) на площадь поверхности S или часть ее. Если этого сделать нельзя, то задачу необходимо решать другими методами. Дипо́ль — идеализированная система, служащая для приближённого описания поля, создаваемого более сложными системами зарядов, а также для приближенного описания действия внешнего поля на такие системы. Дипольное приближение, выполнение которого обычно подразумевается, когда говорится о поле диполя, основано на разложении потенциалов поля в ряд по степеням радиус-вектора, характеризующего положение зарядов-источников, и отбрасывании всех членов выше первого порядка

6 Вопрос- Электростатическое поле - эл. поле неподвижного заряда. Fэл , действующая на заряд, перемещает его, совершая раборту. В однородном электрическом поле Fэл = qE - постоянная величина

Работа поля (эл. силы) не зависит от формы траектории и на замкнутой траектории = нулю.

2.Циркуляцией вектора напряженности называется работа, которую совершают электрические силы при перемещении единичного положительного заряда по замкнутому пути L

Так как работа сил электростатического поля по замкнутому контуру равна нулю (работа сил потенциального поля), следовательно циркуляция напряженности электростатического поля по замкнутому контуру равна нулю.

7 Вопрос

1.Потенциал электростатического поля

-энергитическая характеристика эл. поля. - равен отношению потенциальной энергии заряда в поле к этому заряду. - скалярная величина, определяющая потенциальную энергию заряда в любой точке эл. поля.

Величина потенциала считается относительно выбранного нулевого уровня.

1. ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ - поверхности, все точки которых имеют одинаковый потенциал

для однородного поля - это плоскость

для поля точечного заряда - это концентрические сферы

Эквипотенциальная поверхность имеется у любого проводника в электростатическом поле, т.к. силовые линии перпендикулярны поверхности проводника. Все точки внутри проводника имеют одинаковый потенциал ( =0). Напряженность внутри проводника = 0, значит и разность потенциалов внутри = 0.

39…………Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него. Электромагнитная индукция была открыта Майклом Фарадеем 29 августа 1831 года[1]. Он обнаружил, что электродвижущая сила (ЭДС), возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.

Закон Фарадея

EL=-дельтаФ/дельтаt Е-ЭДСсамоиндукции дельта ф скорость изменения манитного потока

Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э. Х. Ленца:

Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.

40…………Самоиндукция — это явление возникновения ЭДС индукции в проводящем контуре [1] при изменении протекающего через контур тока.

При изменении тока в контуре пропорционально меняется[2] и магнитный поток через поверхность, ограниченную этим контуром[3]. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.

Это явление и называется самоиндукцией. (Понятие родственно понятию взаимоиндукции, являясь как бы его частным случаем).

Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током). Явление самоиндукции проявляется в замедлении процессов исчезновения и установления тока[4].

При сопоставлении силы электрического тока со скоростью в механике и электрической индуктивности с массой в механике ЭДС самоиндукции сходна с силой инерции.

Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока(переменного)

Es=-L*dI/dt I-ток.в.контуре L-индуктивность.контура t- время

18.Сторонние силы,ЭДС,закон Ома для неоднор участка цепи.

Ст силы - силы неэлектрической природы, вызывающие перемещение эл зарядов внутри источника постоянного тока от точки с меньшим потенциалом к точке с большим потенциалом. Характеристикой сторонних сил является ЭДС (Ɛ). 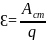/ Это физ величина равная отнош-ю работы ст сил по перемещ-ю положит-го единичного заряда к величине этого заряда.

Закон Ома. На неоднор участке цепи дейст-ют элекростатич и сторонние силы. Тогда и . Получим (закон Ома в дифференц. форме) (в интегральной форме) -разность потенциалов начальной и конечной точек участка цепи, -ЭДС, ( )-полное сопротивление цепи

19. Закон Ома для полной цепи.

Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.

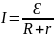
41.1)Вихревое электрическое поле это индуцированное электрическое поле. Переменное магнитное поле порождает наведенное (индуцированное) электрическое поле. Если магнитное поле постоянно, то индуцированного электрического поля не возникает. Следовательно, индуцированное электрическое поле не связано с зарядами, как в случае электростатического поля; его силовые линии не начинаются и не заканчиваются на зарядах, а замкнуты сами на себя, подобно силовым линиям магнитного поля.

 2) Максвелла уравнения могут быть записаны в интегральной или в дифференциальной форме (ниже они даны в абсолютной системе единиц Гаусса. Первое Максвелла уравнения является обобщением на переменные поля эмпирического Ампера закона о возбуждении магнитного поля электрическими токами. Первое Максвелла уравнения имеет вид: ,  то есть циркуляция вектора напряжённости магнитного поля вдоль замкнутого контура L (сумма скалярных произведений вектора Н в данной точке контура на бесконечно малый отрезок dl контура) определяется полным током через произвольную поверхность S, ограниченную данным контуром. Здесь j_n — проекция плотности тока проводимости j на нормаль к бесконечно малой площадке ds, являющейся частью поверхности S,   — проекция плотности тока смещения на ту же нормаль, а с = 3×10¹⁰ см/сек — постоянная, равная скорости распространения электромагнитных взаимодействий в вакууме.

42. 1) Ток смещения, или абсорбционный ток — величина, прямо пропорциональная скорости изменения электрической индукции. Для установления количественных соотношений между изменяющимся электрическим полем и вызываемым им магнитным полем Максвелл ввел в рассмотрение ток смещения. Максвелл высказал гипотезу, что магнитное поле порождается не только токами, текущими в проводниках, но и переменными электрическими полями в диэлектриках или вакууме. Величина, пропорциональная скорости изменения электрического поля во времени, была названа Максвеллом током смещения. Ток смещения возбуждает магнитное поле по тому же закону, что и ток проводимости .Полный ток, равный сумме тока проводимости и тока смещения, всегда является замкнутым. Максвелл определил плотность тока смещения в виде: ,где   ‑ вектор электрического смещения (именно название этого вектора дало название току смещения).Теперь сумму тока проводимости и тока смещения можно назвать полным током. Его плотность: .

2)  Второе Максвелла уравнения является математической формулировкой закона электромагнитной индукции Фарадея записывается в виде: то есть циркуляция вектора напряжённости электрического поля вдоль замкнутого контура L (эдс индукции) определяется скоростью изменения потока вектора магнитной индукции через поверхность S, ограниченную данным контуром. Здесь B_n — проекция на нормаль к площадке ds вектора магнитной индукции В; знак минус соответствуетЛенца правилу для направления индукционного тока.

26.Сила Лоренца – сила, действующая на точечную заряженную частицу, движущуюся в магнитном поле. Сила Лоренца — векторная величина. Сила Лоренца принимает своё наибольшее значение когда векторы индукции и направления скорости частицы перпендикулярны (α=90°).Направление силы Лоренца определяют по правилу левой руки. F=q*v*B*sinα Здесь F – сила Лоренца, q – заряд частицы, B – модуль вектора индукции магнитного поля, v – скорость частицы,α – угол между вектором индукции магнитного поля и направления движения.

27.Закон Ампера показывает, с какой силой действует магнитное поле на помещенный в него проводник. Эту силу также называют силой Ампера.

Формулировка закона: сила, действующая на проводник с током, помещенный в однородное магнитное поле, пропорциональна длине проводника вектору магнитной индукции, силе тока и синусу угла между вектором магнитной индукции и проводником.

F=B*I*l*sinα где α — угол между векторами магнитной индукции и тока,B — индукция магнитного поля,I — сила тока в проводнике, l — длина проводника.

24. Закон Био –Савара- Лапласа определяет величину модуля вектора магнитной индукции в точке выбранной произвольно находящейся в магнитном поле.

это формула определяет модуль вектора dB. где альфа это угол между векторами элементарного участка цепи dl и радиус-вектором r.

Формулировка закона Био Савара Лапласа имеет вид: При прохождении постоянного тока по замкнутому контуру, находящемуся в вакууме, для точки, отстоящей на расстоянии r0, от контура магнитная индукция будет иметь вид.

где I     ток в контуре гамма контур, по которому идет интегрирование,  r0    произвольная точка.

25. Расчет прост магн полей. Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения, магнитная составляющая электромагнитного поля^.

А) Вектор напряженности магнитного поля-Кроме того индукции   часто в расчетах пользуются вектором напряженности   магнитного поля. Если вектор индукции   характеризует суммарное магнитное поле, созданное как током (макротоком), так и микротоками среды, то вектор   описывает магнитное поле, созданное только током. Эти вектора взаимосвязаны:

Б)Для вектора напряженности также справедлив принцип суперпозиции магн.полей : Поле прямолинейного тока-Индукцию магнитного поля бесконечного прямолинейного тока, на расстоянии r от него, мы уже вычисляли и получили результат