Розділ 2. Сингулярно збурені моделі типу “конвекція-дифузія-масообмін”

2.1. Асимптотичне наближення розв’язків сингулярно збурених крайових задач процесів міграції речовини двома шляхами

Розглянемо процес конвективної гетеродифузії для області , де ( ) – двозв’язна криволінійна область (пористий пласт), обмежена двома замкненими гладкими контурами – внутрішній та  – зовнішній (рис. 2, а), який описується такою модельною задачею [10]:

, (2.1.1)

, (2.1.2)

, , , ,

, , (2.1.3)

, , , , (2.1.4)

де – концентрація розчинної речовини фільтраційної течії в точці в момент часу , – концентрація розчинної речовини на поверхні скелету (у зв’язаних зі скелетом поляризованих шарах води), – біжуча точка відповідної кривої, , , , , , де , , , , – задані додатні дійсні числа, ( )– малий параметр (що характеризує переваги одних складових процесу над іншими), – відповідно потенціал та компоненти його швидкості (швидкості фільтрації в пористому середовищі ), , , –

а) б)

Рис. 2. Фізична область (а) та відповідна їй область

комплексного потенціалу (б)

концентраційні коефіцієнти інтенсивності процесів переходу з одного шляху міграції на інший [19], ( ), , , , , , – достатньо гладкі функції, узгоджені між собою на ребрах області .

Дана модель враховує той факт, що частинки розчинної речовини одного сорту у межах виділеного фізично малого елемента ґрунту можуть знаходитись на поверхні скелету чи бути в розчині фільтраційної течії (рис.3) (за умови локальної рівноваги стосовно переходів домішкових частинок між адсорбованими на скелеті ґрунту долями води та в об’ємі скелету причому явища конвекції та сорбції переважають над іншими складовими процесу.

Рис. 3. Структура фізично малого елемента ґрунту:

1 - водний поровий розчин фільтраційного потоку;

2 - адсорбовані на скелеті ґрунту шари води;

3 - скелет ґрунту.

Припустивши, що шляхом конформного відображення (або ), задача (2.1.4) є розв’язаною, вважаємо відомим поле швидкості . Здійснивши заміну змінних , у рівняннях (2.1.1), (2.1.2) та умовах (2.1.3), приходимо до відповідної “гетеродифузійної задачі” для області (рис. 2 б):

, (2.1.5)

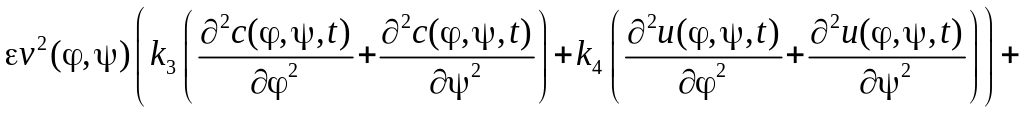
, (2.1.6)

, , ,

, , . (2.1.7)

Розв’язок (c, u) даної періодичної щодо змінної  задачі з точністю (для спрощення викладок покладемо ) шукаємо у вигляді таких асимптотичних рядів:

, (2.1.8)

(2.1.9)

де – залишкові члени, , ( ) – члени регулярної частини асимптотики. , – функції типу пограншару в околі (поправки на виході фільтраційної течії із даного пласта ), – функції типу пограншару в околі (поправки на вході в ). , , 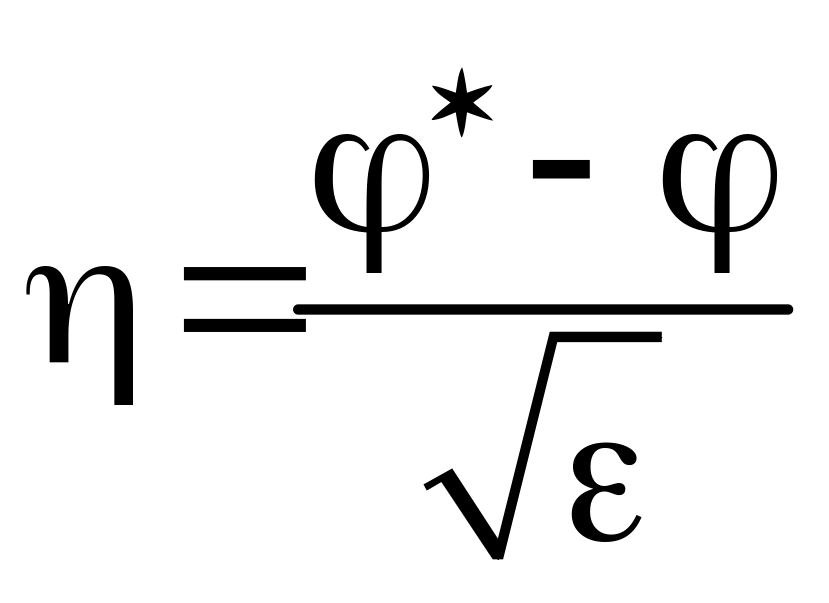– відповідні регуляризуючі перетворення.

В результаті підстановки (2.1.8) та (2.1.9) у (2.1.5), (2.1.6) і виконання стандартної процедури “прирівнювання” коефіцієнтів при однакових степенях , одержимо такі задачі для знаходження та , та оцінки залишкових членів:

де ,

,

.

В результаті їх послідовного розв’язання матимемо:

,

,

де – час проходження виділеної частинки вздовж лінії течії , від точки до точки , – функція обернена до функції стосовно змінної .

Функції , , 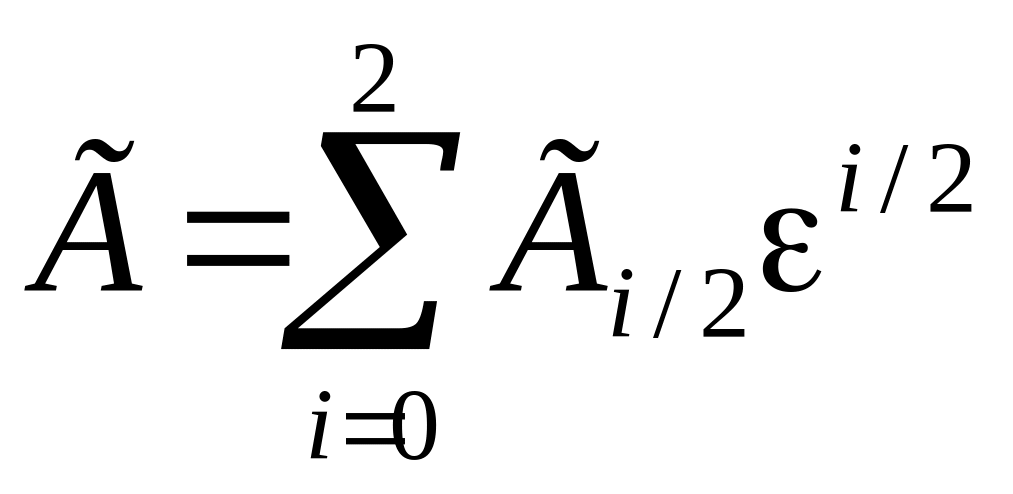призначені для усунення неузгодженостей, внесених побудованими регулярними частинами 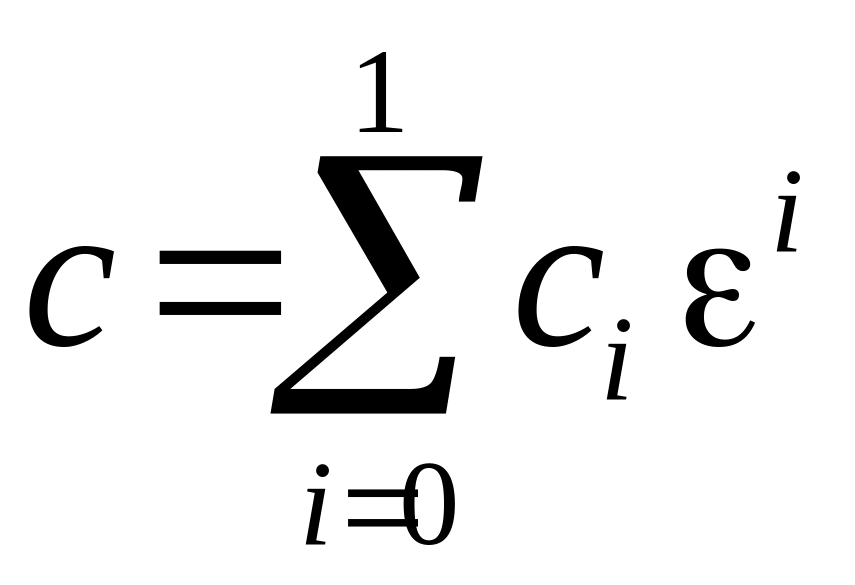, в околах ділянок , (виходу та входу фільтраційної течії). Тобто, повинні виконуватись умови: , , . Для знаходження цих функцій маємо задачі:

;

;

де , , , , , , , , , , , , , ,

,

, ,

,

,

,

.

.

Розв’язки останніх задач, як задач для звичайних диференціальних рівнянь другого порядку та параболічних рівнянь із сталими коефіцієнтами (із параметром ), отримуємо в явному вигляді.

Для знаходження залишкових членів маємо задачу:

,

,

,

де

,

.

Вимагаючи достатню гладкість початкової та граничних умов і коефіцієнтів системи рівнянь (2.1.1), (2.1.2) (існування неперервних частинних похідних до четвертого порядку включно) та їх узгодженість вздовж ребер , паралелепіпеда ( – фіксований проміжок часу), на основі принципу максимуму приходимо до справедливості такого твердження:

( , ).