Курсовой проект Задача о трёх телах / Метод Рунге

Курсовой проект по дисциплине ЧИСЛЕННЫЕ МЕТОДЫ

Метод Рунге-Кутты-Фельберга

Афанасьев Сергей А-13-08

Метод Рунге-Кутты-Фельберга

Теория

Методы Рунге-Кутты являются модифицированными методами Эйлера. Они служат для численного решения обыкновенных дифференциальных уравнений и их систем. Наиболее часто реализуется и используется метод Рунге-Кутты 4 порядка точности. Построение схем более высокого порядка приводит к громоздким расчетам и сопряжено с большими вычислительными трудностями. Схема Эйлера, является представителем семейства схем Р-К. Построение схем основано на разложении функции в ряд Тейлора вблизи инвариантной точки, и взятие конечного числа членов разложения.

Пусть дана задача

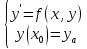
Тогда приближенное решение задается формулой

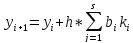
Где h – величина шага сетки, а k вычисляется по формуле

…..

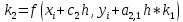
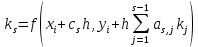
Метод определяется числом s и коэффициентами b_i, a_i,j и c_i

Причем

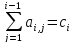
Порядок аппроксимации (точнее порядок сходимости) определить сложно, однако можно определить количество этапов, необходимых для реализации метода.

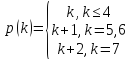
Конкретно метод Р-К 4 для системы ДУ

имеет следующий вид.

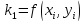
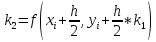
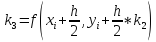
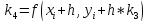
По сути, берется значение методом Эйлера, и уточняется 3 раза. За счет этого возрастает точность вычислений, ценой вычислительных трудностей.

Для метода Рунге-Кутты 5 порядка уравнения будут такими:

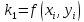
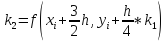
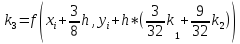
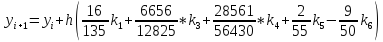
Стоит сказать и об адаптивных процедурах. В ходе выполнения процедуры, шаг, для достижения необходимой точности в следующей точке, выбирается автоматически.

Метод Рунге-Кутты-Фельберга, заключается в том, что на каждом шаге метода точность функции определяется разностью значений между результатами методов РК-4 и РК-5 (Поэтому этот метод иногда называют РК-45). Если они отличаются не более чем на ε – локальную погрешность, то значение, уточненное по Рунге, считается приближенным значением функции в точке на рассматриваемом шаге.

Реализация

Программа, реализующая адаптивную процедуру Рунге-Кутты 4 порядка. Написана программа на языке Delphi в среде Code Gear 2009

//Класс для метода Рунге-Кутты-Фельдера.

TRunge = class

private

Erange: integer; //кол-во функций в системе

Estart: TRealArr; //Начальные значения

EFirst, ELast: double; //Начальное и конечное значение по оси t

Eeps: double; //Точность

Efun: TArrfun; //Массив функций

EArr: TResArr; //Массив значений функции в точках, больше 0.

EArrNeg: TResArr; //Массив значений функции в точках, меньших 0

EGetInd: integer; //Внутренняя переменная - для быстрого поиска нужного значения

procedure SetRange(const Value: integer); virtual;//Установить количество функций в системе

function GetStart(Index: Integer): double; //Получить начальное значений для функции index

procedure SetStart(Index: Integer; const Value: double);//Установить начальное значение value для функции index

function GetRes(X: double; index: integer): double; //Узнать значение функции index в точке x

function GetResInd(X: double): TRealArr; //Узнать значение всех функций в точке x

function GetCount: integer; //Узнать общее количество точек

function GetLeftInd: integer; //Узнать номер самой левой точки в массиве

function GetRightInd: integer; //Узнать номер самой правой точки

function Value(const x: real; const y: TRealArr; const h: real): TRealArr; //Вычисление значения в следующей точке методом РК-4

function Value5(const x: real; const y: TRealArr; const h: real): TRealArr;//Вычисление значения в следующей точке методом РК-5

procedure SetEps(const Value: double); virtual; //Установить значение точности

function calc(vlast: double; veps: double): TRes; overload; virtual; //Процедура вычисления значения в точке vlast с точностью veps

public

property LeftInd: integer read GetLeftInd; //Левый индекс

property RightInd: integer read GetRightInd; // Правый индекс в массиве точек

function GetInd(v: integer; n: integer): double; //Узнать значение функции v в точке n

property Count: integer read GetCount; //Доступ к количеству точек в результате

property Arr[X: double]: TRealArr read GetResInd; default; //Доступ к значениям функции в точке x

property ArrInd[X: double; index: integer]: double read GetRes; //Доступ к значению конкретной функции index в точке x

property range: integer read Erange write SetRange; //Доступ к количеству функций

property Start[Index: integer]: double read GetStart write SetStart; //Доступ к начальным значениям

property First: double read Efirst write EFirst; //Начальное значение по оси t

property Last: double read ELast write ELast; //Конечное значение по оси t

property eps: double read EEps write SetEps; //Точность вычисления

property Fun: TarrFun read EFun write EFun;//Доступ к массиву функций

constructor Create; virtual;

function Calcat(vfirst, vlast, veps: double): boolean; //Вычислить значение на отрезке с точностью

procedure ProcessMessages;

function CheckDelat(n: integer; f: TFunReal): double; //Проверить отклонение полученной функции от реальной.

end;

Класс TGraphicsRunge = class(TRunge) нужен для изображения графика.

Классы

//Класс для исходной задачи

TProg1 = class(TRunge)

public

constructor Create; override; //В конструкторе описываем те входные данные, которые требуется использовать в конкретной задаче

end;

//Два класса для тестовых примеров

TProg2 = class(TRunge)

public

constructor Create; override;

end;

TProg3 = class(TRunge)

public

constructor Create; override;

end;

Конкретные задачи. В конструкторе определяются начальные условия.

Реализация метода Рунге-Кутты-Фельберга

//Вычисленние одного шага методом Р-К 4

function TRunge.Value(const x: real; const y: TRealArr; const h: real): TRealArr;

var i: integer; //счетчики

k: array of TRealArr;

begin

setlength(k, 4, Erange);

setLength(Result, Erange);

for i:=0 to Erange - 1 do k[0, i]:=Efun[i](x, y);

for i:=0 to Erange - 1 do k[1, i]:=Efun[i](x+h/2, inc(y,h*k[0, i]/2));

for i:=0 to Erange - 1 do k[2, i]:=Efun[i](x+h/2, inc(y,h*k[1, i]/2));

for i:=0 to Erange - 1 do k[3, i]:=Efun[i](x+h, inc(y,h*k[2, i]));

for i:=0 to Erange - 1 do result[i]:=y[i]+h*(k[0, i] + 2* k[1, i]+ 2*k[2, i]+ k[3, i])/6;

end;

function TRunge.Value5(const x: real; const y: TRealArr; const h: real): TRealArr;

var i: integer; //счетчики

k: array of TRealArr;

begin

setlength(k, 6, Erange);

setLength(Result, Erange);

for i:=0 to Erange - 1 do begin

k[0, i]:=EFun[i](x, y);

k[1, i]:=EFun[i](x + 1/4*h, inc(y, h*k[0,i]/4));

k[2, i]:=EFun[i](x + 3/8*h, inc(y, h*(3/32*k[0,i] + 9/32*k[1,i])));

k[3, i]:=EFun[i](x + 12/13*h, inc(y, h*(1932/2197*k[0,i] - 7200/2197*k[1,i] + 7296/2197*k[2,i])));

k[4, i]:=EFun[i](x + h, inc(y, h*(439/216*k[0,i] - 8*k[1,i] + 3680/513*k[2,i] - 845/4104*k[3,i])));

k[5, i]:=EFun[i](x + h/2, inc(y, h*(- 8/27*k[0,i] + 2*k[1,i] - 3544/2565*k[2,i] + 1859/4104*k[3,i] - 11/40*k[4,i])));

result[i] :=y[i] + h*(16/135*k[0,i] + 6656/12825*k[2,i] + 28561/56430*k[3,i] +2/55*k[4,i]-9/50*k[5,i]);

end;

end;

//Проверка,

function checkeps(const a,b: TRealArr): double;

var i: integer;

begin

if length(a) <> length(b) then raise Exception.Create('Неверная длина массива. calc.CheckEps: a-'+inttostr(length(a))+', b-'+inttostr(length(b)));

result:=abs(a[0]-b[0]);

for i := 1 to high(a) do result:=max(result, abs(a[i] - b[i]));

end;

//Выполнение одного шага, со всеми проверками

function TRunge.calc(vlast, veps: double): TRes;

var

h, hmin: double;

Arr: PResArr;

procedure Step;

var tmp, tmp2: TRes;

i: integer;

delta: double;

begin

//Текущее значение функции

tmp.arr:=value(Arr^[High(Arr^)].x,Arr^[High(Arr^)].arr,h);

tmp.x:=Arr^[High(Arr^)].x+h;

tmp2.arr:=value5(Arr^[High(Arr^)].x,Arr^[High(Arr^)].arr,h);

tmp2.x:=tmp.x;

//Если функция по точности нам подходит

delta:=checkeps(tmp2.arr,tmp.Arr)*abs(ELast-EFirst)/abs(hmin);

if delta < Eeps then begin

hmin:=min(hmin, abs(h));

//То добавляем её в результрующий массив

setlength(Arr^, length(Arr^)+1);

setlength(Arr^[High(Arr^)].Arr, Erange);

for i := 0 to Erange-1 do

Arr^[High(Arr^)].Arr[i]:=tmp.arr[i];

Arr^[High(Arr^)].x:=tmp2.x;

//Если точность хорошая, то увеличиваем длину шага

if delta < Eeps/1000 then

h:=2*h;

end else //Если точность не достигнута, то уменьшаем шаг

h:=h/2;

end;

begin

Last:=vlast;

if veps > 0 then

Eeps:=veps;

h:=(Elast-Efirst)/10;

hmin:=abs(h);

if Elast > EFirst then begin

Arr:=@Earr;

while Arr^[High(Arr^)].x < last do begin

step;

end

end else begin

Arr:=@EarrNeg;

while Arr^[High(Arr^)].x > last do begin

step;

end;

end;

result:=Arr^[High(Arr^)];

end;

В связи с некоторыми особенностями реализации и использованием сторонних компонентов построение фазового портрета в системе координат y(x) для поставленной задачи занимает продолжительное время.

Тесты

Для задачи 1:

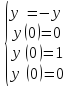
Решением которой будет функция y(x) = sin(x)

Для задачи 2:

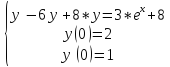
Решением этой задачи коши будет функция y(x) = e^x+ 1

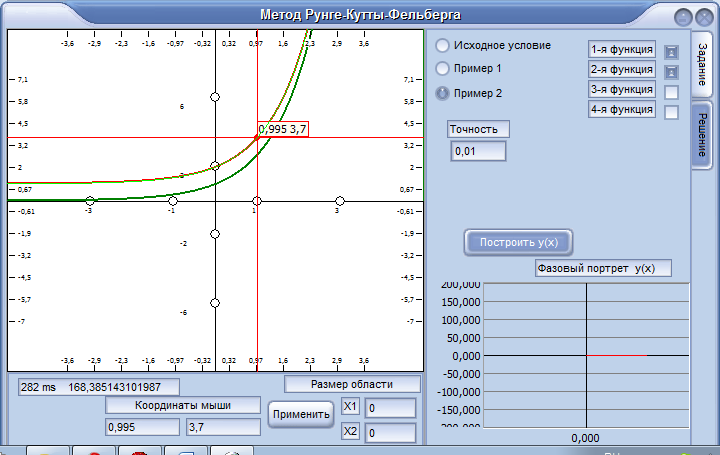
Исходная задача

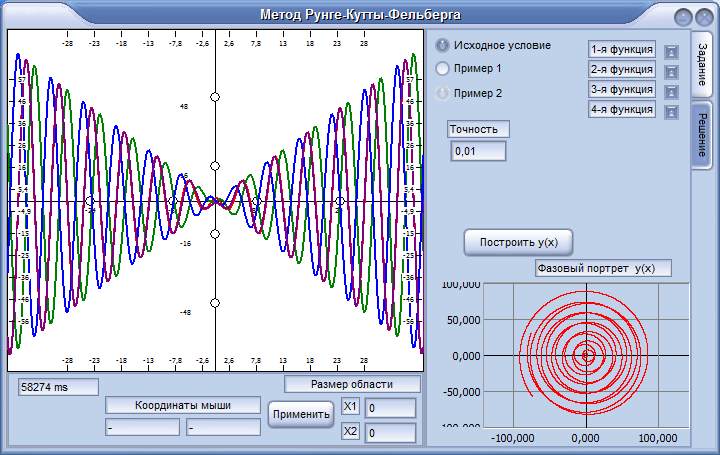
Анализ методов

Далее я хочу сравнить несколько адаптивных процедур Рунге-Кутты.

Сравниваются такие методы:

Метод РК-4 с автоматическим выбором шага

Метод РК-5 с автоматическим выбором шага

Метод РК-45

Сравнение будет проводиться на трех тестах.

a)На задаче

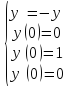
Решением которой будет функция y(x) = sin(x)

b) На задаче

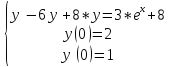
Решением этой задачи коши будет функция y(x) = e^x+ 1

c) и на исходной задаче.

Целью является выяснить коэффициент, в зависимости от которого следует увеличивать шаг, чтобы достичь лучшей скорости вычисления.

Проблема есть и в функции, для перевода глобальной погрешности в локальную. Проблема актуальна, так как для неадаптивной процедуры этим коэффициентом будет ширина шага. Для адаптивной процедуры ширина шага, как таковая не определена, так как шаг переменный. Здесь этим коэффициентом принята величина, равная отношению длины отрезка к ширине наименьшего из сделанных шагов.

Задача а)

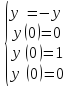
Решением которой будет функция y(x) = sin(x)

Для начала определим наилучший коэффициент, при котором следует увеличивать шаг. Для этого сравним времена вычислений каждой функции на отрезке (-3, 3) с точностью 0,01. В таблицу вынесены основные тесты.

Задача	Коэф.	Рунге-Кутты 4	Рунге-Кутты 5	Рунге-Кутты-Фельберга
Задача А	10	4 ms	2 ms	8 ms
	100	3 ms	2 ms	7 ms
	1000	2 ms	2 ms	8ms
	10000	2 ms	1 ms	7 ms
Задача B	10	24ms	29 ms	20 ms
	100	10 ms	13 ms	20 ms
	1000	1 ms	13 ms	20 ms
	10000	1 ms	13 ms	20 ms
Задача C	10	26 ms	21 ms	95 ms
	100	25 ms	10 ms	100 ms
	1000	25 ms	10 ms	95 ms
	10000	25 ms	10 ms	101 ms

Результаты на относительно малом отрезке при достаточно больших значениях коэффициента отличаются не более чем на 2 ms. Так же зависит и вида функции. Актуальнее всего брать коэффициент 1000 для метода Р-К4.

Для метода РК-5 этот коэффициент особой роли не играет, в связи с этим был проведен эксперимент, в основе которого лежит то, что шаг не может увеличиваться. И на данных тестах результаты не изменились. Это говорит о том, что тестируемые функции имеют очень мало участков с достаточно маленькой производной. На экспоненте метод РК-5 проявил себя не очень хорошо.

Про метод РКФ стоит сказать отдельно. Если в РК4 и РК5 на каждом шаге делалось уточнение по Рунге, то в РК-45 этого сделать нельзя. Так же на каждом шаге производится сравнение разности значений с локальной погрешностью, а не её оценка по правилу Рунге, что тоже повышает точность метода (из-за 2 в степени порядок точности). Так же было замечено, что использование методов РК-4 и РК-5 на больших отрезках на задаче 2 занимают гораздо больше времени, чем использование метода РКФ

Отмечу еще, что мною не была обнаружена явная связь между локальной погрешностью и глобальной. Иными словами не существует гарантий, что метод с заданной точностью достигнет этой точности.

Для этого был проведен еще один эксперимент. В таблице приведены скорости вычислений значений и практическая погрешность. По понятным причинам эксперимент проводился на 2 задачах. На отрезке [-5,5] была задана точность вычисления 0,01, а на отрезке [-1,1] – 0,0001.

Задача	Отрезок	Рунге-Кутты 4	Рунге-Кутты 5	Рунге-Кутты-Фельберга
Задача А	хϵ[-5,5]	4 ms 0,18970	4ms 0,3577	15 ms 0,04494
	хϵ[-1,1]	520 ms 0,001435	12 ms 0,0064	57 ms 0,000698
Задача B	хϵ[-5,5]	1 ms 0,1259…	1 ms 0,228	23 ms 5 разрядов
	хϵ[-1,1]	1 ms 5 разрядов	3 ms 0,0008	82 ms 11 разрядов

Из этой таблицы видно, что метод Рунге-Кутты-Фельберга гораздо точнее, чем два других метода. Так что в следующей таблице приведены результаты вычислений каждым из методов с некоторым изменением. В методах РК-4 и РК-5 проверка достижения точности на каждом шаге оценивается не локальной погрешностью по Рунге, а разностью значений между результатами функций с разными шагами.

Таким образом, была повышена локальная точность.

Задача	Отрезок	Рунге-Кутты 4	Рунге-Кутты 5	Рунге-Кутты-Фельберга
Задача А	хϵ[-5,5]	68 ms 0,0106	98ms 0,01107	15 ms 0,04494
	хϵ[-1,1]	269 ms 0,000207	404 ms 0,00019	57 ms 0,000698
Задача B	хϵ[-5,5]	1 ms 0,004006	7 ms 0,06	23 ms 5 разрядов
	хϵ[-1,1]	1 ms 5 разрядов	71 ms 0,00053	82 ms 11 разрядов

На первой задаче метод РК-45 работает гораздо быстрее двух других методов, однако его точность меньше. На второй задаче обратный результат.

Время вычисления методами РК-4 и РК-5 больше, чем у РКФ, так как на каждом шаге «простой» процедуры помимо вычисления следующего значения, делается пересчет, и в сумме процедура выполняется 3 раза, в то время как в методе РК-45 выполняется вычисление значения методами РК-4 и РК-5 – то есть 2 раза.

У методов РК-4 и РК-5 есть очевидный плюс – пересчет по правилу Рунге, который, как выяснилось и подтвердилось экспериментами, играет очень большую роль.

11