1.2. Обчислення похибки при непрямих вимірюваннях величин

Досить часто трапляється ситуація, коли безпосередньо поміряти значення певної величини неможливо. Проте, знаючи модельну залежність цієї величини

від інших величин (формулу), значення її можна розрахувати. Таке вимірювання називається непрямим.

Наприклад, щоб визначити площу S, ми міряємо його радіус R і обчислюємо площу за формулою:

(2.1)

Як, знаючи точність вимірювання R, оцінити значення похибки S? Точність непрямих вимірювань залежить як від способу вимірювання (формули), так і від точності вимірів усіх величин, які в цю формулу входять.

К.Ф.Гаусс, вважаючи похибку вимірів малою, запропонував лінеаризувати вираз для обчислення результату в околі середніх значень поміряних величин і шукати похибку так, як знаходять повний диференціал функції. Єдина відмінність полягає у використанні того факту, що похибки — завжди додатні величини.

Покажемо підхід Гауса на прикладі функції:

(2.2)

Лінеаризуючи в околі значень отримаємо вираз для обчислення повного диференціала:

(2.3)

Значення часткових похідних, взятих по модулю,

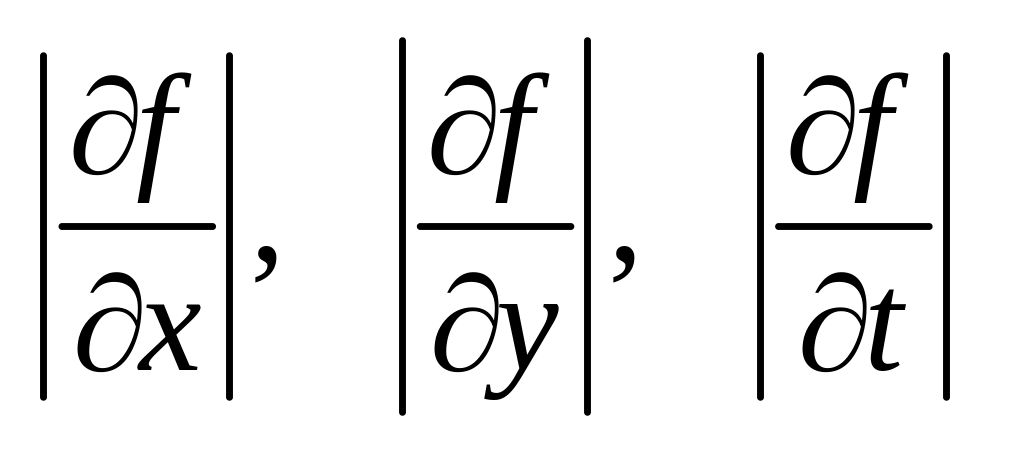(2.4)

в теорії похибок називають чутливостями функції f відповідно до змін величин x, y, t.

Для визначення абсолютної похибки непрямого вимірювання користуються формулою:

(2.5)

тобто, похибку непрямого вимірювання шукають згідно з тими ж правилами, що й повний диференціал цієї величини. Формальна відмінність полягає в тому, що всі арифметичні знаки ± при чутливостях змінюються на знаки +, а знаки диференціалів d – на значки похибок Δ.

Наведемо формули для обчислення абсолютних і відносних похибок:

1. суми:

, (2.6)

2. різниці:

(2.7)

3. добутку:

(2.8)

4. степеня:

; (2.9)

5. дробу:

(3.0)

6. кореня:

. (3.1)

Якщо шукана величина задана виразом, наприклад , то доцільно спочатку прологарифмувати, а потім продиференціювати таким чином:

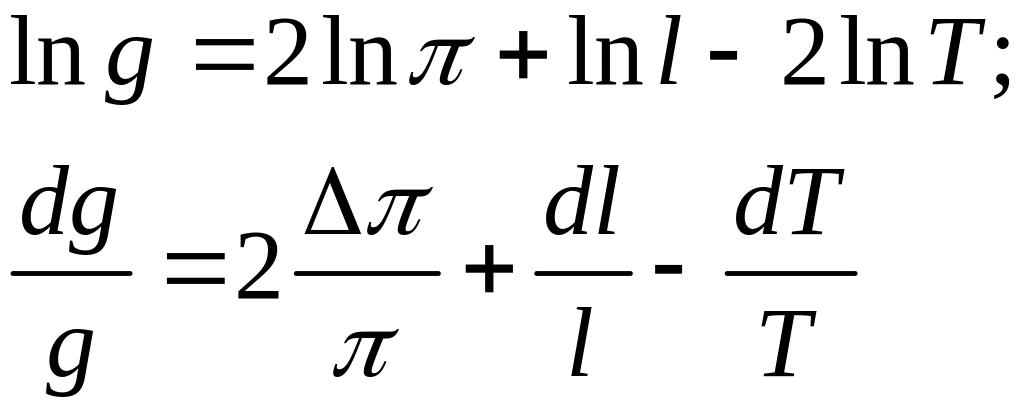
після чого змінити “ ” на “ ” і (-) на (+) :

При практичному використанні такого підходу етап логарифмування можна пропустити, а похибку шукати згідно з правилом: відносна похибка результату дорівнює сумі відносних похибок окремих змінних, взятих з такими коефіцієнтами, в якому степені вони входять у терміни.

№1. ВИВЧЕННЯ ЗАКОНІВ KIHЕMATИКИ I ДИНАМІКИ ПОСТУПАЛЬНОГО РУХУ НА МАШИНІ АТВУДА.

МЕТА РОБОТИ: Перевірити закономірності рівномірного, рівноприскореного руху і другого закону Ньютона.

ОБЛАДНАННЯ: 1)Машина Атвуда,вантажі. 2)Додаткові вантажі. 3)Секундомір.

Теоретичні відомості

Машина Атвуда складається з вертикаль­ної штанги, зверху на якій встановлено 2 легких блоки, що обертаються з незначним тертям. Через блоки перекинута тонка капронова нитка з прикріпленими вантажами однакових мас. На штативі кріпляться платформи:

1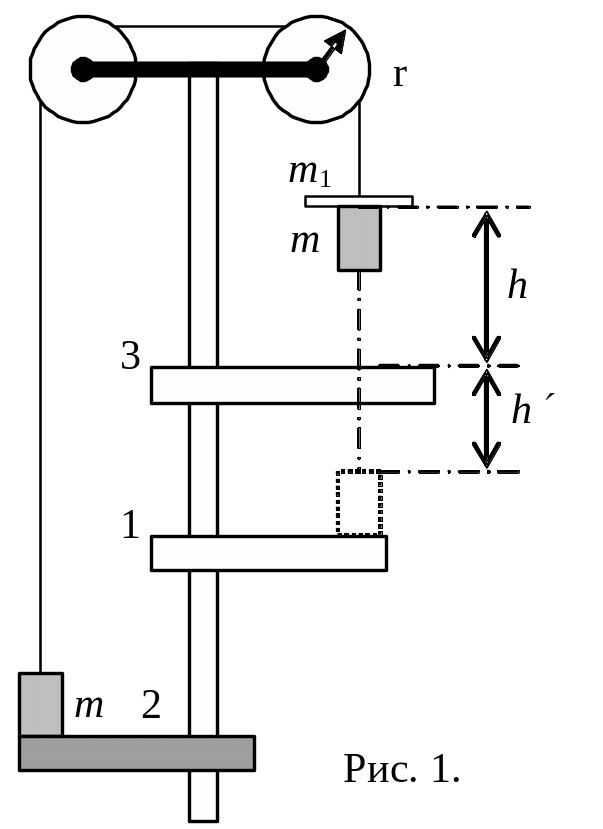 . Суцільна - для визначення кінце­вого моменту руху вантажів;

2. З електромагнітом - для утримання вантажів;

3. Кільцеподібна - для зняття додаткового, вантажу масою під дією якого система приходить в рух.

Розглянемо рух системи, що складається з двох вантажів масою і та блоків радіусом з моментом інерції .

Якщо вантажі одинакові, то потен­ціальна енергія системи не залежить від їх висоти, так як зменшення потенціальної енергії одного вантажу приводить до рівноцінного збільшення потенціальної енергії другого. Отже, потенціальна енергія системи визначається положенням додаткового вантажу масою .

Нехтуючи роботою проти сили тертя на основі закону збереження енергії можна записати:

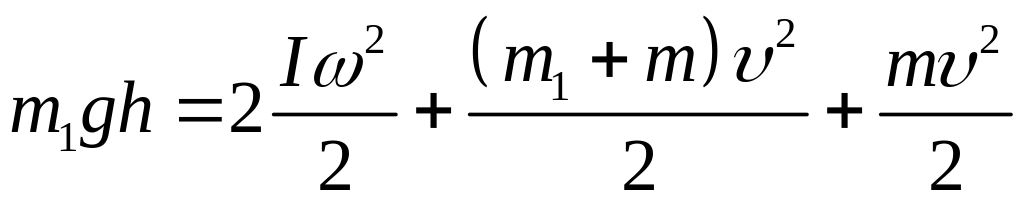, (1)

де: - кінетична енергія блока;

- кінетичні енергії вантажів;

- зменшення потенціальної енергії додаткового вантажу;

- висота, на яку опуститься правий вантаж;

- кутова швидкість обертання блока;

- лінійна швидкість руху вантажів.

Підставляючи значення , , в (1), одержимо:

.

Якщо знехтувати моментом інерції блоків, то формула набере

вигляду:

.