Коефіцієнт поперечного стиску

Деформація подовжнього розтягу супроводжується зменшенням діаметра поперечного перерізу циліндричного зразка на . Відносну зміну називають коефіцієнтом поперечного стиску :

. (5)

Табл. 2.	Речовина	Коефіцієнт Пуассона
	сталь залізо мідь алюміній	0,27 0,27 0,37 0,34

Дослід показує, що відношення коефіцієнтів поперечного стиску до відносного видовження для одного і того ж матеріалу є величина стала:

. (6)

Безрозмірний коефіцієнт називають модулем поперечного стиску, або коефіцієнтом Пуассона. У табл.2 наведено коефіцієнти Пуассона для деяких матеріалів. Для характеристики пружних властивостей ізотропних речовин достатньо задати два модулі пружності – Юнга та Пуассона. Якщо ж речовина анізотропна, їх кількість теоретично зростає до 3⁴= 81.

Деформація зсуву

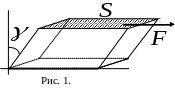Деформацію зсуву можна отримати в паралелепіпеді, якщо одну його грань закріпити, а до протилежної прикласти силу (сколюючу), що лежить у площині цієї грані (див рис. 1). Сколююча сила змушуватиме шари паралелепіпеда ковзати один по одному. Відношення сколюючої сили до площі шару, що зсовується називають сколюючим напруженням

. (7)

Тангенс кута нахилу бокової грані при деформації зсуву називають відносним зсувом. При малих кутах . Дослід показує, що при невеликих деформаціях відносний зсув пропорційний сколюючому напруженню:

. (8)

Коефіцієнт пропорційності називають коефіцієнтом зсуву. На практиці зручніше користуватись величиною, оберненою до коефіцієнта зсуву:

. (9)

Величину називають модулем зсуву. Таким чином, при невеликих деформаціях сколююче напруження пропорційне відносному зсуву:

. (10)

У теорії пружності показано, що модуль зсуву залежить від модуля Юнга та коефіцієнта Пуассона :

. (11)

Деформація згину

Згином називають деформацію, що характеризується викривленням (зміною кривини) осі чи серединної поверхні елемента конструкції (балки, плити та ін.) під дією зовнішнього навантаження (див. рис. 2). При згині зовнішні частини конструкції зазнають деформації розтягу, а внутрішні – деформації стиску. Величину деформації при згинах називають стрілою прогину.

Границі пружності та міцності

В усьому є свої межі; у пружності також. Якщо стержень із досліджуваної речовини поступово навантажувати, вимірюючи відносне видовження, можна побудувати діаграму розтягу, яка наведена на рис. 4. Спочатку деформації пропорційні навантаженням, тобто є пружними. Граничне значення , до якого ще зберігається лінійна залежність від , називають межею пружності.

При навантаженнях, більших межі пружності, починаються пластичні деформації речовини. Зразок видовжується навіть без зміни величини прикладеного навантаження. При відносному видовженні матеріал не витримує розтягу і тіло розривається на частини. Напруження називають межею міцності.

Існують речовини, в яких відсутні пластичні деформації. Такі речовини називають крихкими. У крихких речовин межа міцності збігається з межею пружності.