26

Фальк В.Н.

Элементарное введение в -исчисление

Москва 2007

1. ВВЕДЕНИЕ. 3

2.λ-ИСЧИСЛЕНИЕ 4

3.МОДЕЛИРОВАНИЕ В -ИСЧИСЛЕНИИ КОНСТРУКТИВНЫХ ОБЪЕКТОВ И ВЫЧИСЛИМЫХ ФУНКЦИЙ. 14

4.АЛГОРИТМИЧЕСКИ НЕРАЗРЕШИМЫЕ ПРОБЛЕМЫ В -ИСЧИСЛЕНИИ. 22

5.ИСЧИСЛЕНИЕ КОМБИНАТОРОВ. 25

Издание рекомендуется для самостоятельной работы студентов по дисциплинам «Специальные разделы теории программирования», «Теория вычислительных процессов», «Специальные разделы теории языков программирования». РГСУ, 2007.

1. Введение.

-Исчисление представляет собой формальную систему, базирующуюся на предложенной А. Черчем идее -нотации функций. При определении функций с помощью выражений, определяющих их значения, аргументы традиционно записывались в той же нотации, которая использовалась и для вызова значения определяемой функции для фактических значений ее аргументов, т.е. либо в скобочной функциональной нотации, либо в бесскобочной нотации, обычно, префиксной. Примеры таких традиционных определений:. В качестве альтернативы А. Черч предложил нотацию, в которой в левой части определения указывается только имя определяемой функции, а список ее аргументов перенесен в правую часть определения. Для приведенных выше примеров это выглядит так:.-нотация позволяет также отказаться от рассмотрения функций арности: предполагается, что такая функция имеет единственный аргумент, а ее значением, в свою очередь, является функцияаргументов:, причем при единственном аргументе отпадает необходимость и в использовании разделяющей точки (если символы переменных представляют собой неделимые языковые конструкции).-Нотация функций естественным образом решает вопрос о подстановке определений функции вместо вызовов для вычисления ее значений с конкретными значениями параметров, позволяя рассматривать операцию применения функции к аргументу (аппликацию) как обычную связку. Нетрудно заметить, что-операция функциональной абстракции в конструкцииимеет явные черты оператора, связывающего операторную переменнуюв выражении, описывающем значение конструируемой функции. Как будет видно из дальнейшего, язык, построенный с применением единственной бинарной связки (аппликации) и единственного-оператора (при наличии потенциально бесконечного множества различных переменных), может играть рольуниверсальной формальной модели вычислимости, обладая при этом новыми интересными особенностями, не присущими традиционным моделям – теории частично-рекурсивных функций и различным математическим уточнениям понятия алгоритма. Базирующаяся на -исчислении теория комбинаторов выглядит еще более «фундаментальной», сохраняя черты универсальности при большей синтаксической простоте.

2. Λ-исчисление

   1. Λ-Термы.

Для построения -термов (далее просто термов, сорт объектов ) необходимо счетное множество переменных, для чего конструируются натуральные числа (вспомогательный сорт объектов).

Для построения натуральных чисел используются два конструктора: и, а для построения термов – три конструктора:,и.

Далее будет использоваться обычное для описания -исчисленияпредставление:

Название конструкции		Конструкция объекта	Представление
Номер переменной			Представление числав десятичной системе счисления
Терм	Терм-переменная (- номер переменной)
	Функциональный терм (– термы)
	Терм-аппликация (– номер переменной,– терм)

Для некоторых доказательств мы будем пользоваться понятием -контекста (сорт объектов ); для построения контекстов дополнительно вводится нульарный конструктор. Порождаемый им элементарный контекст будем представлять «дыркой» – символом.. Для построения других контекстов будем использовать конструкторы и представление, подобное представлению термов:

,

,

,

.

Если – контекст, а– терм, тобудет обозначать терм, полученный заменой вединственного символа на терм . Еслии– контексты, тообозначает контекст, полученный заменой в контекстеединственного символа на контекст .

Вхождением терма в термназывается пара, такая, что. Различные вхождения одного и того же термав один и тот же термотличаются вторыми компонентами соответствующих пар, т.е. контекстами вхождений.

На множестве термов определена функция :называетсямножеством свободных переменных терма и определяется индуктивно по конструкции терма:

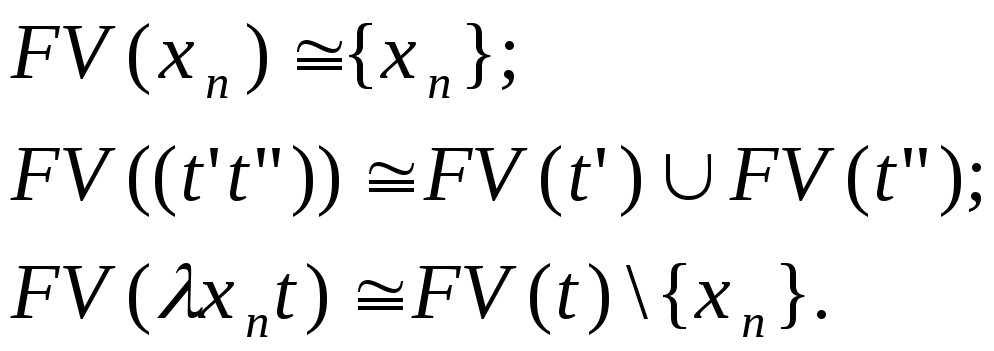
Иными словами, свободной переменной терма называется терм-переменная (или, просто, переменная), имеющая в него хотя бы одно свободное вхождение, т. е.

.

Введем операцию подстановки: .

назовем результатом подстановки терма в термвместо свободных вхождений в него терма-переменнойи определим его индуктивно по конструкции терма:

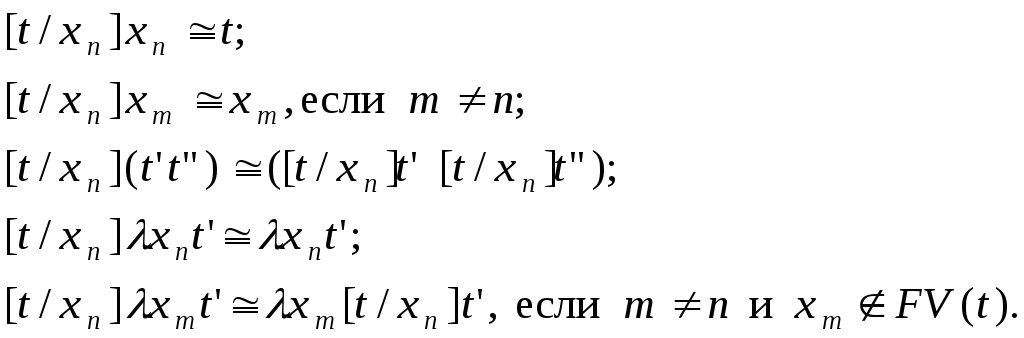
Случай , пока оставим не определенным.