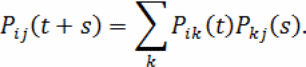Федеральное Государственное Образовательное Учреждение

Высшего профессионального Образования

Якутская Государственная Сельскохозяйственная Академия

Инженерный Факультет

Кафедра «Математики и Кибернетики»

Реферат на тему:

«Методы массового обслуживания»

Выполнили: ст. 4 курса гр. Зем-13А

Саввин Александр Юрьевич

Якутск 2017

Содержание

Введение

1. Основные понятия теории массового обслуживания

1.1 Цепь Маркова и Марковские процессы

1.2 Теория массового обслуживания

1.3 Сеть массового обслуживания

2. Мультипликативность стационарного распределения в открытых сетях с многорежимными стратегиями обслуживания

2.1. Основная модель

.1.1 Обслуживание заявок

.2 Уравнения равновесия

.3 Уравнения трафика

Заключение

Список используемой литературы

Введение

Одним из важных разделов экономико-математического моделирования является теория массового обслуживания, представляющая собой теоретические основы эффективного конструирования и эксплуатации систем массового обслуживания. Системы массового обслуживания (СМО) встречаются во многих областях экономики (производство, техника-военная область, быт и др.) и предназначены для многократного использования при выполнении однотипных задач.

Основоположником теории массового обслуживания считается датский ученый А. К. Эрланг. Являясь сотрудником Копенгагенской телефонной компании, он опубликовал в 1909 году работу «Теория вероятностей и телефонные переговоры», в которой решил ряд задач по теории систем массового обслуживания с отказами. Значительный вклад в создание и разработку общей теории массового обслуживания внес выдающийся советский математик Александр Яковлевич Хинчин (1984 - 1959), который предложил сам термин теория массового обслуживания. В зарубежной литературе чаще используется название теория очередей.

В 1957г. Дж.Р.Джексон впервые ввел в рассмотрение понятие открытой сети массового обслуживания, а в 1967г. Гордон и Ньюэлл ввели аналогичное понятие замкнутой сети. В отличие от системы массового обслуживания сеть представляет собой более сложное образование, состоящее из систем массового обслуживания, называемых узлами сети, которые взаимодействуют между собой с помощью некоторого вероятностного механизма. В открытых сетях заявки могут поступать извне, а также уходить из сети. В замкнутых сетях сохраняется постоянное число заявок, которые с помощью случайной маршрутизации могут перемещаться между узлами сети; при этом поступление заявок в сеть и уход заявок из сети невозможны.

Состояние сети массового обслуживания обычно характеризуется вектором, координаты которого описывают состояния отдельных узлов сети. В силу многомерности случайного процесса состояний и статистической зависимости между координатами исследование сетей массового обслуживания на порядок сложнее, чем исследование систем массового обслуживания.

Предметом исследования теории массового обслуживания являются вероятностные модели физических систем обслуживания, в которых случайные и не случайные моменты времени возникают заявки на обслуживание и имеются устройства на обработку данных заявок.

1. Основные понятия теории массового обслуживания

1.1 Цепь Маркова и марковские процессы

Цепь Маркoва - последовательность случайных событий с конечным или счётным числом исходов, характеризующаяся тем свойством, что при фиксированном настоящем будущее независимо от прошлого.

Цепь Маркова с дискретным временем - это последовательность дискретных случайных величин , в которой выполняется условие:

Таким образом, в простейшем случае условное распределение последующего состояния цепи Маркова зависит только от текущего состояния и не зависит от всех предыдущих состояний.

Матрица , где

называется матрицей переходных вероятностей на -м шаге, а вектор , где - начальным распределением цепи Маркова.

Цепь Маркова называется одноро́дной, если матрица переходных вероятностей не зависит от номера шага, то есть

В противном случае цепь Маркова называется неоднородной.

Цепь Маркова с непрерывным временем или Марковский процесс - это семейство дискретных случайных величин , в котором выполняться:

Цепь Маркова с непрерывным временем называется однородной, если

Конечномерные распределения однородной цепи Маркова с непрерывным временем полностью определены начальным распределением

и ма́трицей перехо́дных фу́нкций (переходных вероятностей)

Матрица переходных вероятностей удовлетворяет уравнению Колмогорова - Чепмена:

Или