§ 1. Функция нескольких переменных (фнп).
Определение функции нескольких переменных ______________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
График функции 2-х переменных.____________
_________________________________________________________________________________________________________
Л
иния
уровня_________________________
___________________________________
______________________________________________________________________
П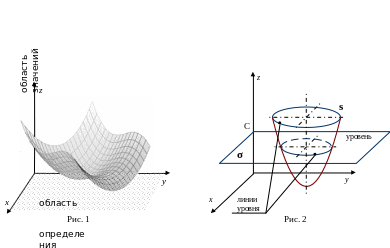
ростейшим
примером функции нескольких переменных,
используемой в экономике, является
производственная
функция.
Производственная функция – зависимость результатов производственной деятельности (выпуска продукции) от обусловивших его факторов – затрат ресурсов.
П
роизводственная
функция двух переменных вида
называется функцией
Кобба-Дугласа.
Параметры α и
β
– частные эластичности выпуска продукции
(постоянные величины) по отношению к
переменным факторам х
и у.
График этой функции представляет собой
некоторую поверхность трёхмерной
системы координат, построение которой
может вызвать определённые сложности.
Но можно значительно упростить задачу,
зафиксировав одну из переменных, как
постоянную, придавая ей определённые
значения.
Пример.
Изменяя величину фонда заработной
платы постройте производственную
функцию
,
где
- объем товарной продукции
в стоимостном выражении, х
- фонд заработной платы (млрд. руб.), у
- стоимость основных
фондов (млрд. руб.).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§ 2. Частные и полное приращения функции двух переменных. Частные производные функции двух переменных.
П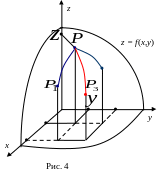
усть
задана функция z
= f(x,y).
Так как х и у – независимые
переменные, то одна из них может
изменяться, а другая оставаться
постоянной. Дадим независимой переменной
х приращение
,
сохраняя значение у неизменным. Тогда
z
получит приращение, которое называют
частным приращением z
по x
и обозначают:
Сформулировать самостоятельно частное приращение z по y ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определение частной производной по х _____________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Частная
производная по х обозначается одним
из символов:
;
;
;
Аналогичным образом даётся следующее определение (самостоятельно)
Определение частной производной по y _____________________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Частная производная по у обозначается одним из символов: _______________________
Пример.
Найти частные производные
функции двух переменных
по каждой из переменных: х и у.
Решение.
Производную
найдём, считая х переменной, а
у постоянной величиной:
Производную
найдём, считая у переменной, а
х постоянной величиной:
