Пример решения задачи № 2

Три однофазных потребителя электроэнергии (рис. 3.3) включены «звездой» в трехфазную четырехпроводную сеть с симметричным линейным напряжением U_Л = 380 В. Комплексные сопротивления фаз:

Ом;

Ом;

Ом.

Определить

− фазные и линейные токи;

− ток в нейтральном проводе;

− активную мощность каждой фазы

и всей цепи.

Построить

− векторную диаграмму токов

и напряжений.

Решение

Величина сопротивления каждой фазы:

Ом;

Ом;

Ом.

Фазные напряжения «звезды» сети меньше линейных в раз:

В.

При соединении «звезда» линейные токи сети равны фазным

.

A;

A;

A.

Активные мощности в каждой фазе:

Вт;

Вт;

Вт.

Активная мощность всей цепи

Вт.

Величина тока в нейтральном проводе определяется по I закону Кирхгофа

.

Это можно сделать графически по векторной диаграмме путем сложения векторов фазных токов.

П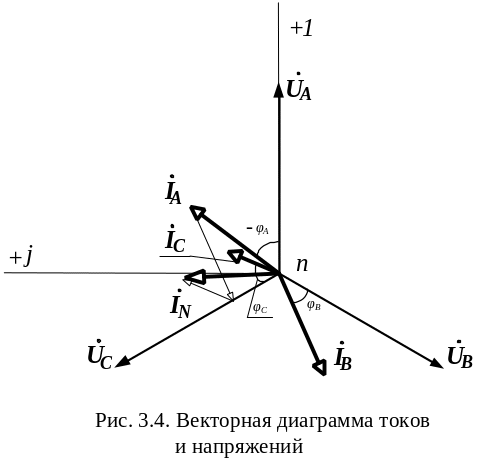 остроение векторной диаграммы (рис. 3.4) надо начинать с построения звезды векторов фазных напряжений.

Для векторов напряжений и токов удобнее принять разные масштабы:

m_U = 10 B / 1 мм,

m_I = 2 A /1 мм.

Вектор фазного напряжения направлен по действительной оси +1. Все векторы фазных напряжений сдвинуты друг относительно друга на 120°.

Для построения векторов фазных токов определяем угол сдвига фаз

.

;

−вектор тока опережает вектор фазного напряжения на 53°.

;

−вектор тока отстает от вектора фазного напряжения на 36°.

.

−вектор тока отстает от вектора фазного напряжения на 53°.

Сложив все векторы токов, получаем вектор тока в нулевом проводе. Измерив его и умножив на масштаб тока, получим значение тока в нулевом проводе:

A.

Пример решения задачи № 3

Трехфазный потребитель электроэнергии с активными и реактивными сопротивлениями R₁ = 10 Oм, R₂ = R₃ = 5Oм и X_L = X_C = 5 Oм фаз соединен «треугольником» (рис. 3.5) и включен в трехфазную сеть с линейным напряжением U_Л = 100 В при симметричном питании.

О пределить

− показания амперметра А при отключении (обрыве) линейного провода L 3 (выключатель В

разомкнут);

− фазные I_Ф и линейные I_Л токи;

− активную Р, реактивную Q

и полную S мощности каждой

фазы и всей электрической цепи

(при замкнутом выключателе В).

Построить

− векторную диаграмму токов и напряжений.

Решение

При обрыве линейного провода L 3 нарушается симметричное трехфазное питание цепи. Фазы ВС и СА соединены последовательно и образуют первую ветвь параллельного участка.

Полное сопротивление первой ветви параллельного участка цепи

Ом.

Т. к. реактивные сопротивления Х_L = X_C, то в цепи возникает резонанс напряжений, и она ведет себя как активное сопротивление (Z₁ = R = 10 Oм).

Общее сопротивление цепи при обрыве линейного провода L 3:

Ом.

Показание амперметра при обрыве линейного провода L 3:

.

Фазные токи потребителя при замкнутом выключателе В:

А;

А;

А.

В екторная диаграмма токов и напряжений с учетом характера нагрузки показана на рис. 3.6.

Выбраны масштабы:

m_U = 0,6 B / 1 мм,

m_I = 0,5 A /1 мм.

Линейные токи определяют из уравнений, составленных по I закону Кирхгофа для каждого узла:

Фазные токи построены с учетом углов сдвига фаз:

, , −

вектор тока сонаправлен с вектором напряжения ;

, −

вектор тока опережает вектор напряжения на 45°;

, −

вектор тока отстает от вектора напряжения на 45°.

Составляющие фазных токов:

Активные

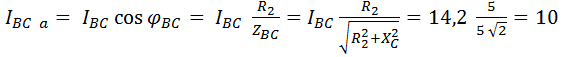А;

А;

А.

реактивные

, т.к. .

А;

А.

Величину линейных токов потребителя электроэнергии определяют исходя из векторной диаграммы, умножая длину вектора на масштаб:

Мощности фаз потребителя:

активные

Вт;

Вт;

Вт.

реактивные

;

ВАр;

ВАр;

где знак минус указывает на емкостный характер мощности.

Полные мощности фаз потребителя:

ВА;

ВА;

ВА.

Мощности всей цепи:

активная

Вт;

реактивная

;

полная

ВА.