Закон сохранения импульса

Из уравнения Δp_с = Δt вытекает следствие: если сумма внешних сил, действующих на систему равна нулю: 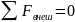, то и Δp_с = 0. Это значит, что какой бы интервал времени мы не взяли суммарный импульс вначале и в конце этого интервала один и тот же: p _{с. к.} – p _{с. н.}

p_c = m₁v₁+m₂v₂+m₃v₃ = const

Закон сохранения импульса:

Если сумма внешних сил, действующих на тела системы равна нулю, то импульс системы сохраняется.

Тела могут только обмениваться импульсами, суммарное же значение импульса не изменяется. Причем, сохраняется только векторная сумма импульсов, а не сумма их модулей.

Закон сохранения импульса является следствием второго и третьего законов импульса.

Законы сохранения справедливы для изолированных систем.

Система тел, на которую не действуют внешние силы, называется изолированной или замкнутой.

В замкнутой системе импульс тела сохраняется.

Реальные системы всегда являются незамкнутыми. Это физическая абстракция. Сумма внешних ил редко обращается в нуль, но все равно во многих случаях закон сохранения импульса можно применять.

Реактивное движение.

Под реактивным движением понимают движение тела, возникающее при отделении некоторой его части с некоторой скоростью относительно тела.

Пример: истечение продуктов сгорания из сопла реактивного летательного аппарата.

Простейший пример: надуть шарик и отпустить: под действием струи воздуха он будет двигаться до тех пор пока весь воздух не выйдет наружу.

При этом и появляется так называемая реактивная сила.

Особенность реактивного движения: возникает без всякого взаимодействия с внешними телами.

Происходит взаимодействие лишь между ракетой и вытекающей из нее струей вещества.

При истечении продуктов сгорания топлива, они за счет давления в камере сгорания приобретают некоторую скорость и, следовательно, некоторый импульс. По закону сохранения импульса ракета приобретает такой же по модулю импульс, но направленный в противоположную сторону.

Когда запускают ракету, то при полете масса ракеты с течением времени убывает и поэтому она в полете является телом переменной массы.

Для расчета ее движения применяют закон сохранения импульса, с помощью которого получается уравнение Мещерского для реактивного движения:

Уравнение Мещерского:

1. В случае, когда ракета движется в космосе, то есть внешние силы не действуют: M 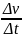= - µu

2. В случае, когда на ракету действуют внешние силы: M = - µu + F

В данном уравнении: M – масса ракеты; v – скорость ракеты ; t - время ; u – скорость вытекающих из ракеты газов ; F – сумма внешних сил, действующих на ракету.

Принцип реактивного движения: Вытекающие из реактивного двигателя газы получают импульс. Такой же по модулю импульс получает ракета.

Закон сохранения энергии

Энергия тесно связана с работой, поэтому ее изучение начинается с работы.

Работа:

Бытовое представление о работе:

Если человек и любой двигатель действуют с определенной силой на движущееся тело, то говорят, что они совершают работу. Бытовое представление о работе только до некоторой степени согласуется с понятием о работе как о физической величине. Например, работа грузчика по подъему грузов является тем большей, чем больше вес того груза, который он поднимает и, чем больше высота, на которую он этот груз поднимает. С бытовой точки зрения люди называют физической работой всякую деятельность человека, при которой он совершает некоторые мускульные усилия. С точки зрения механики такая деятельность может и не сопровождаться работой. В древнегреческом мифе об Атланте, который якобы держит на своих плечах небесный свод, люди имели в виду огромные усилия, которые для этого требуются, и расценивали эти усилия, как колоссальную работу. С точки зрения науки механики здесь никакой работы не совершается, и мышцы атланта можно заменить просто какой-нибудь колонной или подставкой.

Это бытовое представление о работе легло в основу одного из важных понятий механики – понятия работы силы.

Работа в природе совершается всегда, когда на любое движущееся тело действует сила (или силы) со стороны другого тела (или тел). Таким образом, любая сила совершает работу. Например, сила тяжести совершает работу при падении капель дождя или падении камня. Одновременно с ней совершает работу и сила трения, которая действует на капли дождя и камень со стороны воздуха.

При некоторых условиях работа может и не совершаться при действии на тело отдельной силы.

Второй закон Ньютона: Δp = FΔt позволяет определить, каким скорость тела изменяется по модулю и направлению, если на тело в течение времени Δt действует сила F.

Во многих случаях необходимо уметь вычислять изменение скорости по модулю, если при перемещении тела на него действует сила.

Действия сил на тело, приводящее к изменению модуля их скоростей, характеризуется величиной, зависящей как от сил, так и от перемещений тел, на которые эти силы действуют. Эту величину называют работой.

М еханической работой называют физическую величину, равную произведению модуля силы на модуль перемещения тела и на косинус угла между ними. Обозначается работа буквой А.

A = F_r·Δr·cosα, где F_r – проекция (модуль) силы на направление перемещения, Δr - перемещение тела.

A = F· Δr = F_r· Δr ·cosα – работа представляет собой скалярное произведение векторов силы и перемещения.

Таким образом, работа есть скалярное произведение вектора силы на вектор перемещения.

Сама работа является скалярной величиной!!!

Единицей работы является 1 Дж

Работа может быть положительной, отрицательной или равной нулю:

α < 90º	cosα > 0	А – положительная
α >90º	cosα < 0	А – отрицательная
α = 90º	cosα = 0 (сила направлена перпендикулярно перемещению)	А = 0

В природе все силы делятся на два виды – консервативные и диссипативные. Консервативными называются силы, работа которых не зависит от формы траектории (то есть зависит от начальной и конечной точек приложения сил) (например, является сила тяжести). Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется. Диссипативными называются силы, при действии которых на механическую систему ее полная энергия убывает, переходя в другие, немеханические формы энергии, например, в теплоту. Диссипативные силы совершают отрицательную работу, которая приводит к уменьшению энергии системы. Например, сила трения является диссипативной силой и совершает отрицательную работу, так как под воздействием силы трения движение тела постепенно прекращается.

Работа нескольких сил:

Если на тело действует несколько сил, то проекция результирующей силы на перемещение равна сумме проекций отдельных сил:

F_r = F_1r + F_2r + …

Поэтому для работы результирующей силы: A = F_r·Δr = F_1r · Δr + F_2r · Δr + …

Таким образом, если на тело действует несколько сил, то полная работа (работа всех сил) равна работе результирующей силы.

Работа переменной силы на произвольном участке пути:

В данном случае для вычисления работы весь путь разбивается на очень маленькие участки, на каждом из которых действующая сила считается постоянной. Затем находится элементарная работа 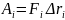на каждом из таких участков, производится суммирование и полная работа на всем пути равна: A = F_r · Δr₁ + F_r · Δr₂ + …