6.Оценка точности измеренных величин и их функций

6.1.Оценка точности результатов измерений по истинным ошибкам

Формулы и обозначения:

m _l = - средняя квадратическая ошибка измерения (6.1)

пред. = 2 m _l - предельная ошибка измерения. (6.2)

m _ml = - средняя квадратическая ошибка величины

(надежность оценки точности). (6.3)

_i = l_i – X - истинная ошибка. (6.4)

где: l_i - результат измерений,

Х­­­ - истинное значение измеренной величины (за истинное значение может быть принято точное, на порядок точнее измерений, значение)

n - число измерений.

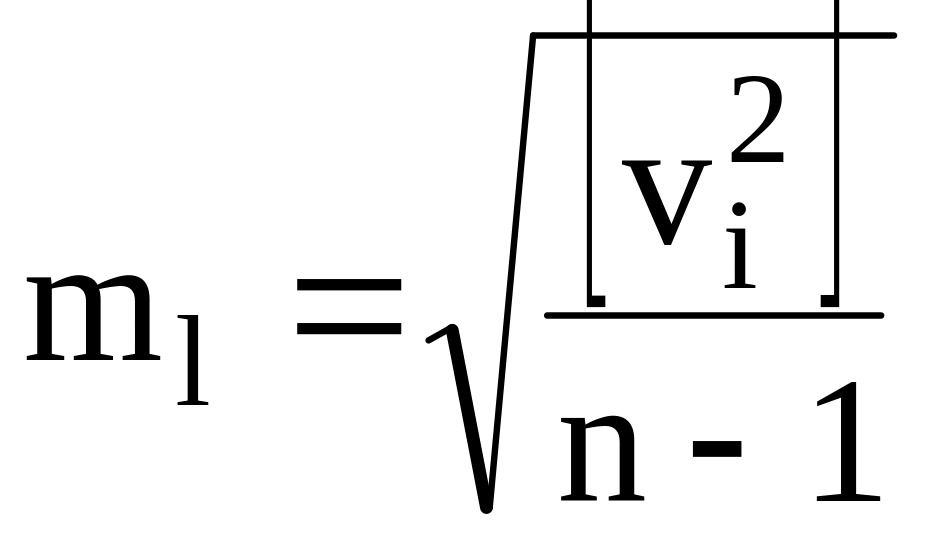- средняя квадратическая ошибка одного измерения (6.5)

- средняя квадратическая ошибка вероятнейшего значения (6.6)

- вероятнейшее значение измеренной величины (6.7)

Vi = L – li - вероятнейшая поправка (6.8),

L – вероятнейшее значение измеренной величины

- средняя квадратическая ошибка величины (6.9)

- средняя квадратическая ошибка величины (6.10)

[V] = L * n - контроль вычислений L и VL. (6.11)

где: n – число измерений.

L = Lокр. – Lточн. - ошибка округления значения L. (6.12)

Задача 6.1.1

При измерении границы земельного участка лентой получены значения l_i (м): 100,01; 100,08; 99,95; 99,90+0,01№ (№ - номер индивидуального задания). Известно значение X = 100,010 м.

Вычислить среднюю квадратическую и предельную ошибки одного измерения и установить надежность оценки.

Задача 6.1.2.

При измерении угла теодолитом получены значения li: 9000,5; 9000,8; 8959,7; 8959,5; 9000,2; 8959,2. Известно значение X = 9000,05.

Вычислить среднюю квадратическую и предельную ошибки одного измерения и установить надежность оценки.

Пример для задач 6.1.

Условие задачи.

При измерении превышения тригонометрическим нивелированием получены значения li(м): 2,46; 2,60; 2,52; 2,50.

Известно значение X = 2,525 м.

Требуется выполнить оценку точности, предусмотренную при решении задач 6.1.1- 6.1.2.

Решение задачи.

Таблица 6.1.

Обработка ряда измерений по истинным ошибкам.

измерения	результат измерений li, м	i = li – X , см	i²
1	2,46	-6,5	42,25
2	2,60	+7,5	56,25
3	2,52	-0,5	0,25
4	2,50	-2,5	6,25
		i = -2,0	i² = 105,00

m _l = = 5,1 см

_пр = 2 * 5,1 = 10,2 см

m_mi = = 2,5 см

6.2.Оценка точности результатов равноточных измерений одной и той же величины

Задача 6.2.1.

При измерении угла на карте получены значения li: 6515'; 6521'; 6512'; 6524'. Найти вероятнейшее значение угла и выполнить оценку точности результатов.

Решение.

Таблица 6.2

Обработка ряда равноточных измерений.

№ измерения	Результат измерения, li	Вероятнейшая поправка,Vi	Vi²
1	6515
2	6521
3	6509
4	6518
	 65 * 4 + 63

Lточн.=

Lокр. =

L =

Контроль: [V] =

m _L =

m_ml =

m_mL =

6.3.Оценка точности функций измеренных величин

Формулы и обозначения.

u = f ( х1, х2, ... хn) - функция нескольких переменных (6.13)

mu =   ( f / xi )² * mXi² - средняя квадратическая ошибка функции нескольких переменных (для линейных функций можно применить более простые формулы), (6.14)

где: f/ xi - частные производные функции по каждой переменной, mi – средняя квадратическая ошибка переменной.

Задача 6.3.1.

Вычислить предельную ошибку и допустимую невязку площади участка, состоящего из трех контуров (при пред=2m), если средние квадратические ошибки площадей контуров равны: m1 = 0,21 га; m2 = 0,15 га; m3 = (0,10 + 0,01 * N ) га.

Задача 6.3.2.

Вычислить предельную ошибку и допустимую невязку суммы n (2 + №) углов теодолитного хода (пред = 2m), если средняя квадратическая ошибка измеренного угла равна m = ( 10 +№ )".

Задача 6.3.3.

Вычислить предельную ошибку (допустимую невязку) суммы n (3 + №) превышений нивелирного хода (пред = 2m), если средняя квадратическая ошибка измеренного превышения равна ( 1 + 0,1х № ) мм.

Задача 6.3.4.

Вычислить предельную ошибку (допустимую невязку) линии, состоящей из четырех отрезков ( пред = 2m ), если средние квадратические ошибки отрезков равны: m₁ = 0,02 м, m₂ = 0,05 м, m₃ = 0,10 м, m₄ = 0,01*№ м.

Пример по задачам 6.3.

Условие задачи.

Вычислить предельную ошибку превышения пред = 2m из тригонометрического нивелирования, если известны средние квадратические ошибки: горизонтального проложения линии S, mS = 0,10 м и вертикального угла , m = 0,5, при S = 100 м и  = 544.

Решение.

Функция (превышение ) : h = S tg 

Частные производные : h/S = tg ,

h/ = S/соs²

Средняя квадратическая ошибка превышения:

m h = √tg² * mS² + S/соs² * m²/ρ² ,

m h =  0,1² * 0,1² + 100² / 0,99002 * (0,5/3438)² = 0,058 м

Предельная ошибка превышения: h = 3 * 0,058 м = 0,17 м

5.4.Веса измерений и их функций

Формулы и обозначения.

Р = С / m² - вес измерения (6.14)

С - произвольное постоянное число для данного ряда измерений

m - средняя квадратическая ошибка измерения

РL = [ Pi ] - вес вероятнейшего значения измеренной величины (6.15)

-обратный вес функции нескольких переменных (6.16)

Задача 6.4.1.

Вычислить вес площади участка, состоящего из трех контуров, если веса площадей контуров равны: 2, 4 и (4+0,1№)

Задача 6.4.2.

Вычислить вес вероятнейшего значения площади участка, полученного по результатам трех измерений с весами: 2, 4 и (4 + 0,1№ ).

Задача 6.4.3.

Вычислить все суммы n (2 + №) углов теодолитного хода, если вес измерения одного угла равен единице.

Задача 6.4.4.

Вычислить вес третьего угла в плоском треугольнике, полученного как разность между 180° и суммой двух других углов, измеренных каждый с весом равным N.

Пример по задачам 6.4.

Вычислить вес суммы углов в треугольнике, если веса измерений каждого из углов соответственно равны 2, 1, 2.

Решение.

Функция:  = 1 + 2 + 3

Частные производные:  / i = 1

Обратный вес суммы углов: 1/Р = 1/2 + 1 + 1/2 = 2

Вес суммы углов: Р = 1/2

6.5.Оценка точности неравноточных измерений одной и той же величины

Формулы и обозначения.

Li - результат измерений

Рi - вес результата измерений

L = [P l] / [P] - вероятнейшее значение измеренной величины (6.17)

- средняя квадратическая ошибка единицы веса (6.18)

m _L = μ /  Р - средняя квадратическая ошибка вероятнейшего

значения (6.19)

- средняя квадратическая ошибка величины (6.20)

μ (надежность оценки)

- средняя квадратическая ошибка величины (6.21)

mL (надежность оценки)