1. Общие положения.

Курсовая работа «Обработка результатов измерений» по дисциплине «Технические измерения и приборы» состоит из расчетно-пояснительной записи, в которой приводятся формулы, используемые в расчетах, а также исходные данные для их выполнения.

В записке приводится форма таблицы, где помещаются результаты расчета.

Состав курсовой работы:

• титульный лист;

• задание;

• содержание (введение, теоретическая часть (Вопрос из варианта), расчетная часть, заключение, список литературы).

Шрифт Times New Roman, кегль 14, интервал 1,5, поля 2 см, абзац 1,25 (1.27), по ширине, перенос автоматический. Объем 25-30стр.

Выполненная согласно стандарту на листах белой бумаги курсовая работа, скрепляется и помещается в мягкую обложку.

Теоретический вопрос в Приложении 1. Исходные данные для расчета указаны в Приложении 2.

Произвести обработку результатов измерений мощности Р с использованием ГОСТ 8.207-76. Причем результат мощности получен с помощью косвенных измерений, а напряжение и сила тока – приямых.

При статистической обработке группы 5 результатов наблюдений следует выполнить следующие операции:

• вычислить среднее арифметическое исправленных результатов наблюдений,

• результат измерения; вычислить оценку среднего квадратического отклонения результата наблюдения;

• вычислить доверительные границы случайной погрешности (случайной составляющей погрешности) результата измерения;

• вычислить границы неисключенной систематической погрешности (неисключенных остатков систематической погрешности) результата измерения;

• вычислить доверительные границы погрешности результата измерения.

I. Обработка результатов прямых измерений

При обработке результатов прямых измерений номер и размерность обрабатываемых физических величин определяется видом математической зависимости:

Р=U*I

Первая физическая величина U (В) 220; 210; 280; 223; 218.

Вторая физическая величина I (А) 10; 9; 11; 19; 9.

Класс точности первого и второго прибора 1

Порядок расчета

1. Обработка первой физической величины (u)

Первой физической величиной является напряжение U,В

1.1 В качестве результата измерения принимаем среднее арифметическое результатов наблюдений U1, U2,... U_n.

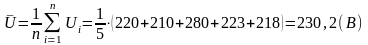(1)

1.2 Вычисляем случайные отклонения результатов наблюдений V_i

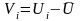(2)

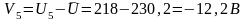
1.3 Для оценки правильности вычисления случайных отклонений, проверяем, близка ли к нулю их алгебраическая сумма.

(3)

Определяем средне квадратическое отклонение результатов наблюдений

(4)

Определяем оценку среднего квадратического отклонения результатов наблюдений

(5)

Результаты заносим в Таблицу 1.

Таблица 1.1 – Результаты измерений и вычислений

№ наблюдения	Ui, B	Vi, B	Vi2, B2
1	220	-10,2	104,04
2	210	-20,2	408,04
3	280	49,8	2480,04
4	223	-7,2	51,84
5	218	-12,2	148,84

1.4 Для оценки принадлежности Umin и Umax к данной нормальной совокупности и принятия решения об исключении либо нет Umin (Umax) в составе выборки, найдем отношение:

(6)

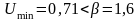
(7)

β=1,6 – максимальное допустимое отклонение (для 5 измерений)

Так как , то результат наблюдения анормален и должен быть исключен из результатов измерений. Исключаем анормальный результат и повторяем обработку результатов измерений, начиная с пункта 1.1.

1.5 В качестве результата измерения принимаем среднее арифметическое результатов наблюдений U1, U2,... U_n.

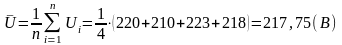
1.1.7 Вычисляем случайные отклонения результатов наблюдений, среднеквадратичное и оцениваем его ( формулы 2,3,4,5)

Результаты измерений заносим в Таблицу 2.

Таблица 2 – Результаты измерений и вычислений

№ наблюдения	Ui, B	Vi, B	Vi2, B2
1	220	2,25	5,06
2	210	-7,75	60,06
3	223	5,25	27,56
4	218	0,25	0,06

Определяем оценку среднего квадратического отклонения результатов наблюдений

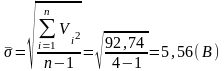
1.8 Для оценки принадлежности Umin и Umax к данной нормальной совокупности и принятия решения об исключении или оставлении Umin(Umax) в составе выборки найдем отношение:

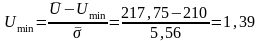
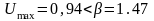
β=1,47 - максимальное допустимое отклонение (для 4 измерений)

Так как и 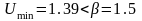, то результат наблюдений нормален.

1.9 Находим оценку среднего квадратического отклонения результата измерения

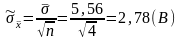(8)

1.10 Задаем доверительные границы случайной погрешности результата измерений (ψ)

,

где t- коэффициент Стьюдента

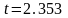(приложение 3)

1.11 Определяем абсолютную погрешность Δ

Не исключенная систематическая погрешность

,

где γ=1 – класс точности прибора

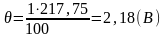
Так как 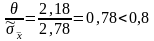, то погрешностью средства измерения по сравнению со случайными погрешностями пренебрегаем и принимаем, что граница результата (абсолютная погрешность

1.12 Запись результата производим по ГОСТ 8.011-72 при систематической доверительной погрешности результатов измерений ±, с вероятностью Р(t).

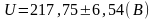с вероятностью р(t) = 0,95