
- •Основы теории вероятностей и математической статистики Вероятность.
- •Случайная величина, её функция распределения. Математическое ожидание и дисперсия случайной величины Факториал
- •Формула Бернулли
- •Наивероятнейшее событие
- •Случайные величины
- •Дискретные случайные величины.
- •Математическое ожидание
- •Дисперсия
- •Непрерывные случайные величины
- •Элементы математической статистики Полигон и гистограмма
Случайные величины
Определение:
Величина, которая в зависимости от случая может принимать различные числовые значения, называется случайной. Данная величина характеризуется значениями, которые она может принимать, и вероятностями, с которыми эти значения принимаются.
Дискретные случайные величины.
Определение:
Случайная
величина, которая принимает значения
х1,
х2,
…, хn,
… соответственно с вероятностями р(х1),
р(х2),
… , р(хn),
…
![]() называется дискретной
(прерывной).
называется дискретной
(прерывной).
Пусть Х – случайная величина и х – произвольное действительное число. Тогда вероятность того, что Х примет значение меньшее, чем х , называется функцией распределения вероятностей данной случайной величины Х.
-
Х
0
1
2
…
n
Р(х)
 qn
qn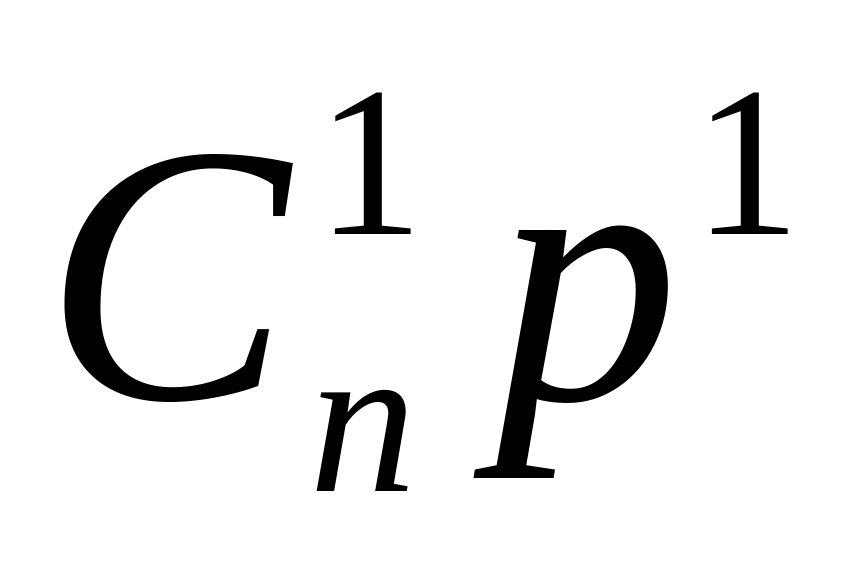 qn-1
qn-1 qn-2
qn-2…
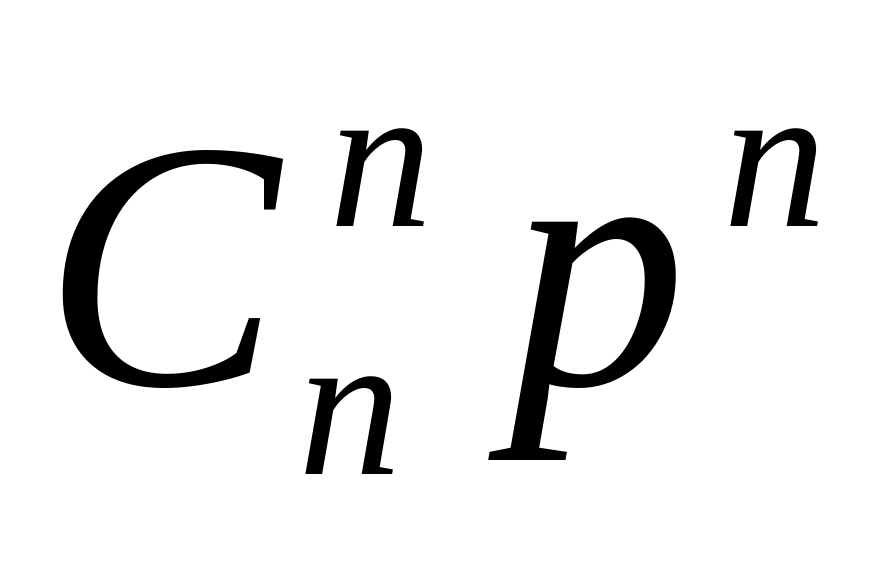 q0
q0
p – вероятность наступления события в отдельном испытании
q = 1 – p.
n – число испытаний,
k– число благоприятных исходов (k = от 0 до n),
Х – случайная величина,т.е. k
Р(х) – функция распределения вероятностей данной случайной величины Х
Задача № 7.
Стрелок производит 3 выстрела по мишени. Вероятность попадания в мишень при каждом выстреле равна 0,4. Построить функцию распределения вероятности попадания в мишень.
Решение:
Пусть событие А – это удачный выстрел, тогда
p = P(A) =0,4, q = 1 − 0,4 = 0,6,
n = 3,
k =0; 1; 2; 3
Р(х) вычисляем по формуле Бернулли:
-
Х
0
1
2
3
Р(х)
0,216
0,432
0,288
0,064
Математическое ожидание
Определение:
Математическое ожидание – величина равная приближённо среднему арифметическому наблюдаемых значений случайной величины (при большом n).
М(Х)
=
![]()
Дисперсия
Определение:
Дисперсией
(рассеянием) дискретной случайной
величины называется математическое
ожидание квадрата отклонения случайной
величины от её математического
ожидания. ![]()
Задача №8.
Монета подбрасывается 2 раза.
Построить функцию распределения вероятности выпадения герба. Найти математическое ожидание данной случайной величины и дисперсию данной случайной величины.
Решение:
Пусть событие А – это выпадение герба, тогда
p = P(A) = , q = 1 − = ,
n = 2,
k =0; 1; 2 (герб может выпасть 0 раз, 1раз, 2 раза)
Р(х) вычисляем по формуле Бернулли:
1)
k
= 0 : ![]() 2)
k
= 1:
2)
k
= 1: ![]()
3)
k
= 2: ![]()
-
Х
0
1
2
Р(х)
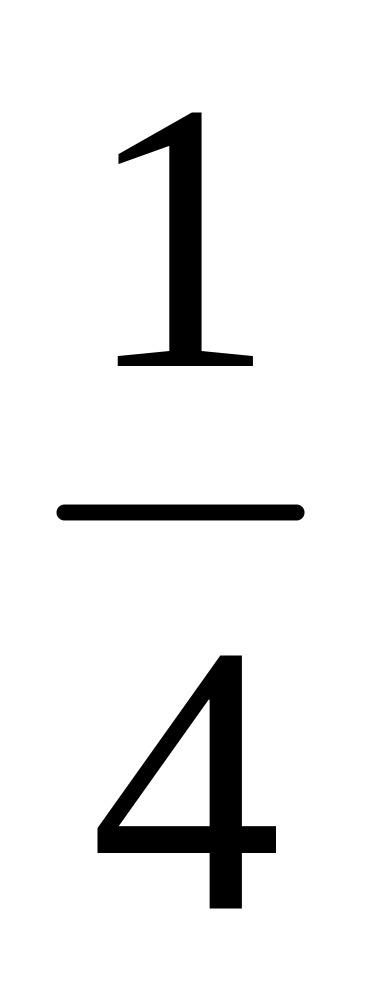
математическое ожидание данной случайной величины равно:
![]()
дисперсия данной случайной величины равна:
D(Х) =1/4(0 – 1)2 +1/2(1 – 1)2 + 1/4(2 – 1)2 = 1/2
