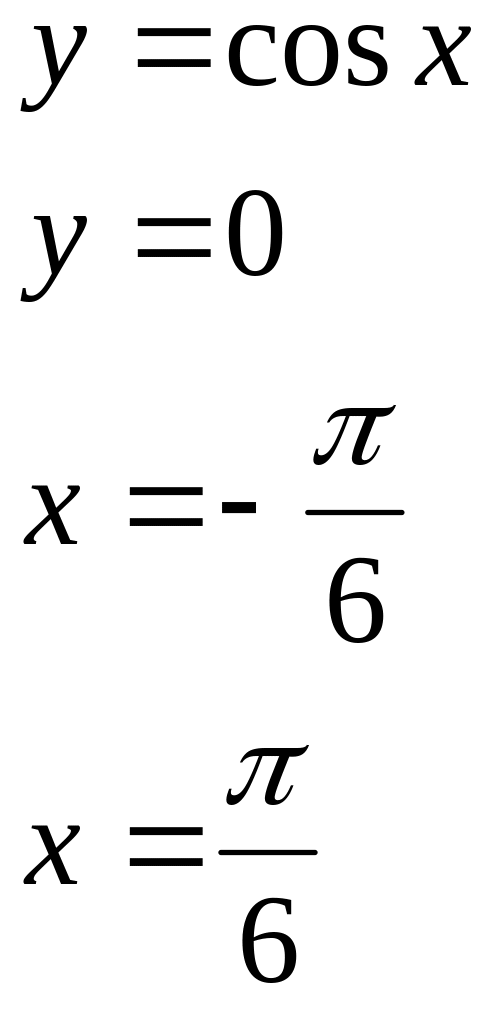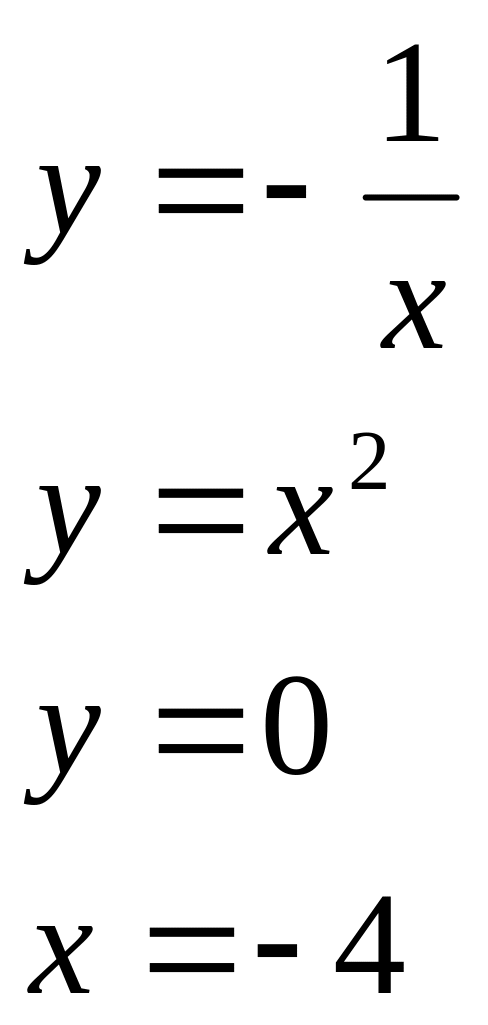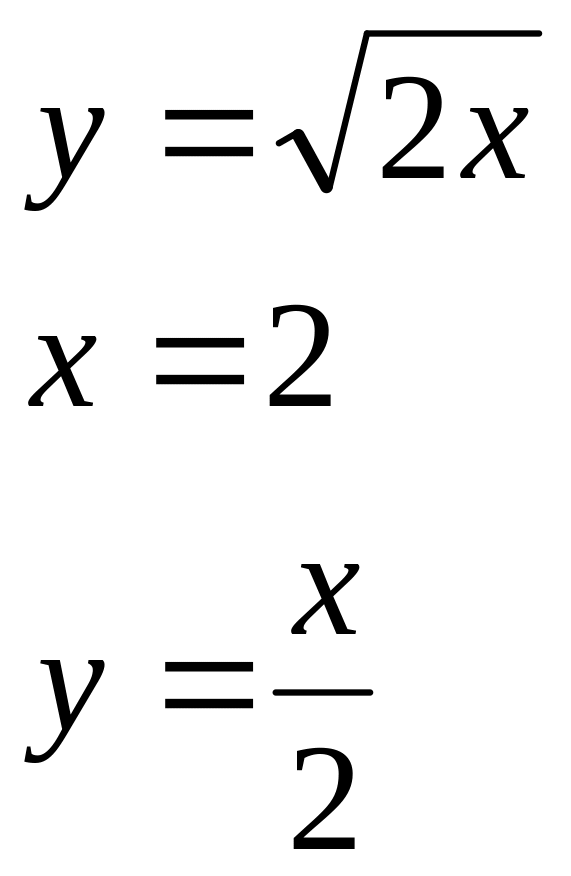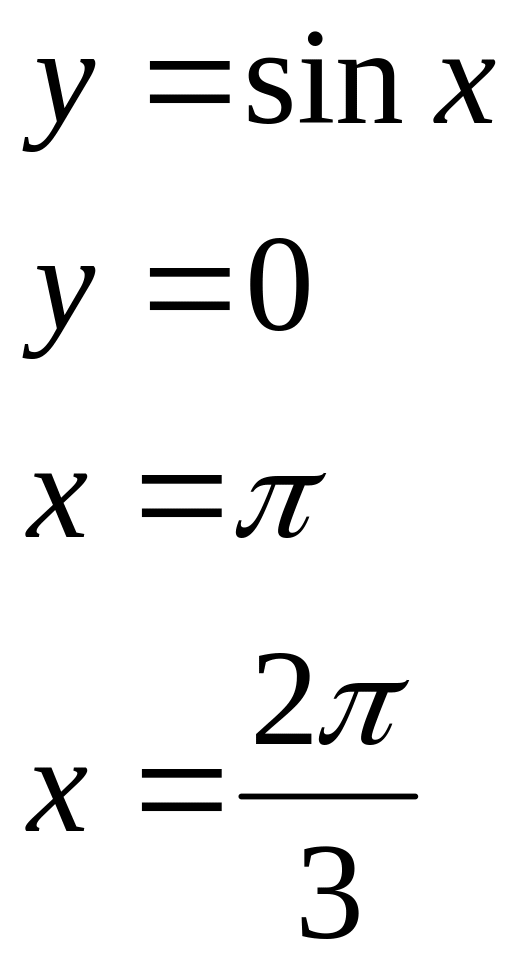Площадь криволинейной трапеции
Фигура,
ограниченная функцией
![]() прямыми х =
а , х
= b
и осью Ох называется криволинейной
трапецией.
прямыми х =
а , х
= b
и осью Ох называется криволинейной
трапецией.

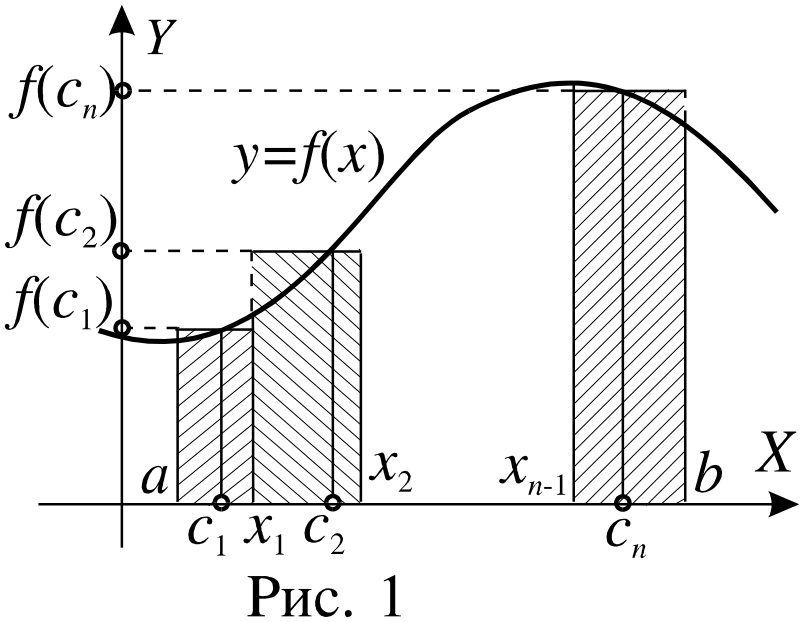
Разобьем
отрезок
![]() на n
частей точками
на n
частей точками
![]() .
.
При
этом криволинейная трапеция разобьется
на
![]() элементарных криволинейных трапеций.
Заменим каждую такую криволинейную
трапецию прямоугольником с основанием
элементарных криволинейных трапеций.
Заменим каждую такую криволинейную
трапецию прямоугольником с основанием
![]() ,
где
,
где
![]() и высотой
и высотой
![]() ,
где
,
где
![]() -произвольно
выбранная внутри отрезка
-произвольно
выбранная внутри отрезка
![]() точка.
точка.
Площадь
прямоугольника будет равна
![]() ,
а площадь всей криволинейной фигуры
приблизительно будет равна сумме
площадей всех прямоугольников:
,
а площадь всей криволинейной фигуры
приблизительно будет равна сумме
площадей всех прямоугольников:
![]() .
.
Выражение
![]() ,
где
,
называется интегральной суммой функции
,
где
,
называется интегральной суммой функции
![]() на отрезке
.
на отрезке
.
Если
существует конечный
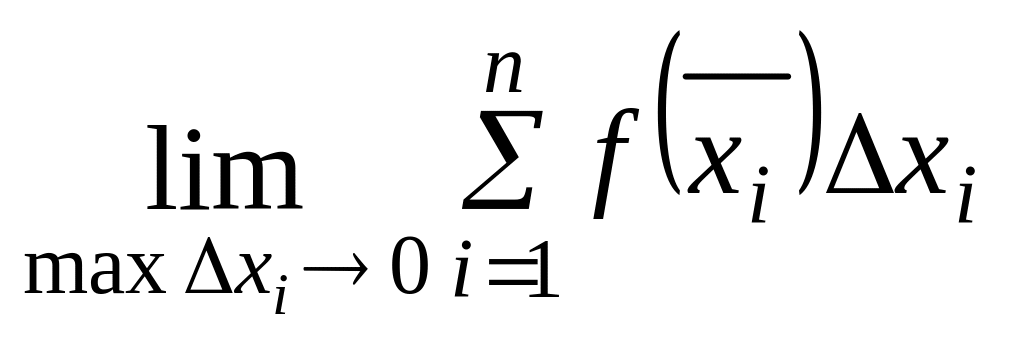 , не зависящий ни от способа разбиения
отрезка
, не зависящий ни от способа разбиения
отрезка
![]() на
части, ни от выбора точек
на
части, ни от выбора точек
![]() , то этот предел называется определенным
интегралом функции
, то этот предел называется определенным
интегралом функции
![]() на отрезке
и обозначается
на отрезке
и обозначается
![]() .
.
С
геометрической точки зрения при
![]() равен
площади криволинейной трапеции
равен
площади криволинейной трапеции
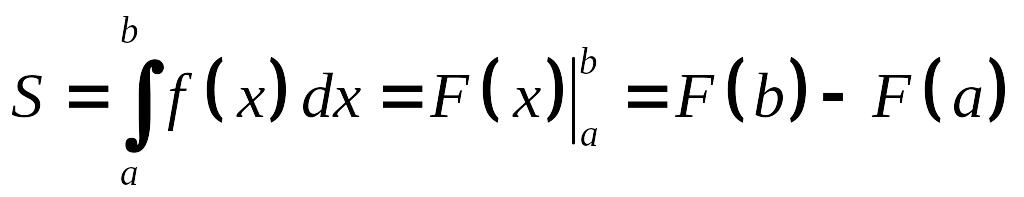
Число a называется нижним пределом интегрирования, а число b верхним пределом интегрирования.
Вид криволинейной трапеции:
Рассмотрим фигуру, ограниченную графиком непрерывной, неотрицательной на промежутке [a;b] функции f(x), отрезком [a;b] оси X, и прямыми x = a; x = b. Такую фигуру называют криволинейной трапецией. На рисунке 2 криволинейная трапеция выделена штриховкой. Площадь S этой трапеции определяется формулой
I .
.
![]() .
II.
.
II.
![]()

III.
![]()

I V.
V.
![]()
Пример 1. Вычислить площадь фигуры, ограниченной графиками функций y=x2 – 2x+2 и y=2+6x – x2.
 Решение.
Решение.
1) Выполняем чертеж;
2) Найдем пределы интегрирования:
x2–2x+2=2+6x–x2, откуда х=0 – нижний предел интегрирования
и х=4 – верхний предел интегрирования (ВПИ);
3) Составим подынтегральную функцию:
f(x)=2+6x–x2 – (x2–2x+2)=8x–2x2;
![]() (кв.ед.)
(кв.ед.)
Пример 2
Вычислить площадь фигуры, ограниченной линиями
![]()
![]() и
и
![]()
![]()
![]()
![]()
![]()
![]()

Пример 3. Вычислить площадь фигуры, ограниченной графиками функций y=x+3, y= x– и y= –2x+9.
Решение.
1) Выполняем чертеж
Для дальнейшего решения необходимо разбить полученную фигуру на две части: DABD и DBCD.
2) Найдем пределы интегрирования: а) x+3= –2x+9 Þ x=2;
б) x+3= x– Þ x=−5; в) −2x+9= x− Þ x=4.
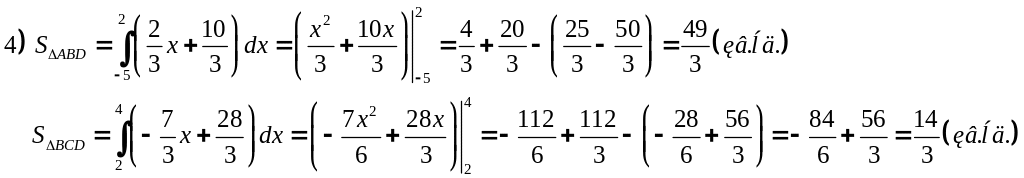
(кв.ед.)
(кв.ед.)
Значит, Sфигуры=SDABD+SDBCD=21 (кв.ед.)
П ример
4.
Вычислить площадь фигуры, ограниченной
графиками функции y=2x2–8х
и двумя касательными к данному графику,
проходящими через точку (2; –10)
ример
4.
Вычислить площадь фигуры, ограниченной
графиками функции y=2x2–8х
и двумя касательными к данному графику,
проходящими через точку (2; –10)
Решение.
1) Выполняем чертеж;
Найдем абсциссы точек касания, используя формулу касательной к графику функции y=f(x) в точке х0: y=f'(x0)(x−x0)+f(x0).
y'=4x−8, −10=(4x0−8)(2−x0)+2x0−8x0 ,откуда х0=1 или 3. Построим касательные.
Для дальнейшего рационального решения достаточно вывести уравнение только одной касательной, например, АВ: y=−4(х −1)−6, т.е. y=−4х−2. Тогда, при пределах интегрирования х=1 и х=2, площадь половины фигуры равна:
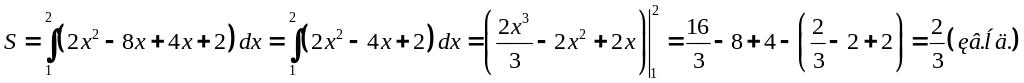
(кв.ед.)
(кв.ед.)
Значит, площадь всей фигуры равна:
![]()
Упражнения для самопроверки
№ 1. Найти неопределённые интегралы:
1.![]() 2.
2.![]()
3. 4.
5.![]() 6.
6.![]()
7.![]() 8.
8.![]()
9.![]() 10.
10.![]()
11.![]() 12.
12.![]()
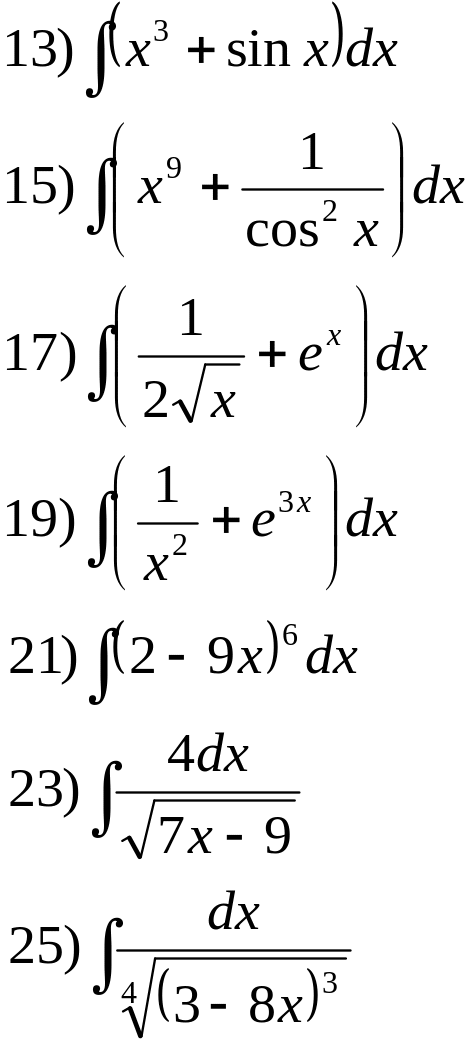
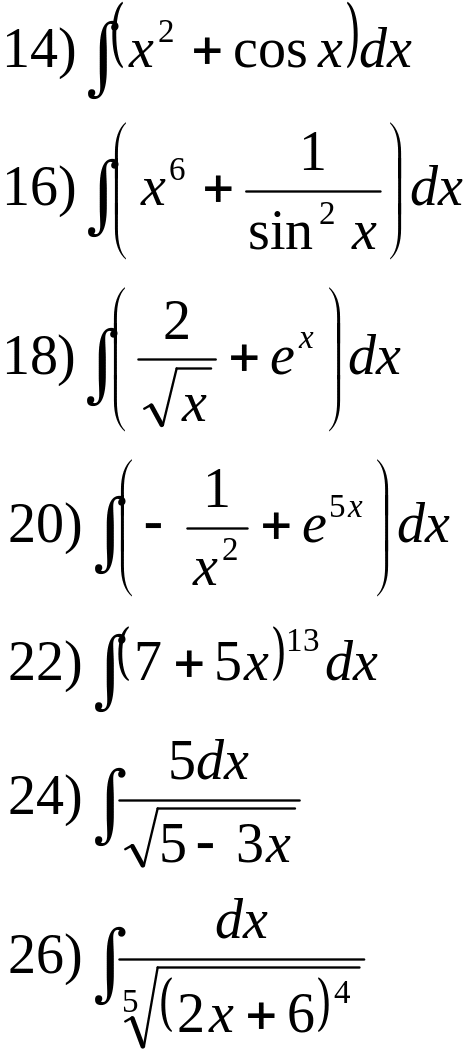
№ 2. Проинтегрировать по частям:
1.![]() 2.
2.![]()
3. 4.
№ 3. Найти определённый интеграл:
1.
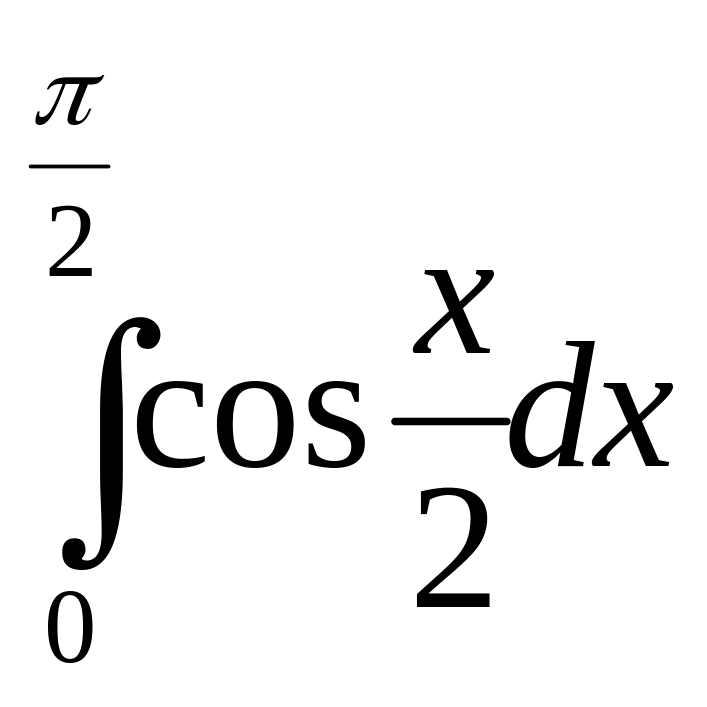 2.
2.
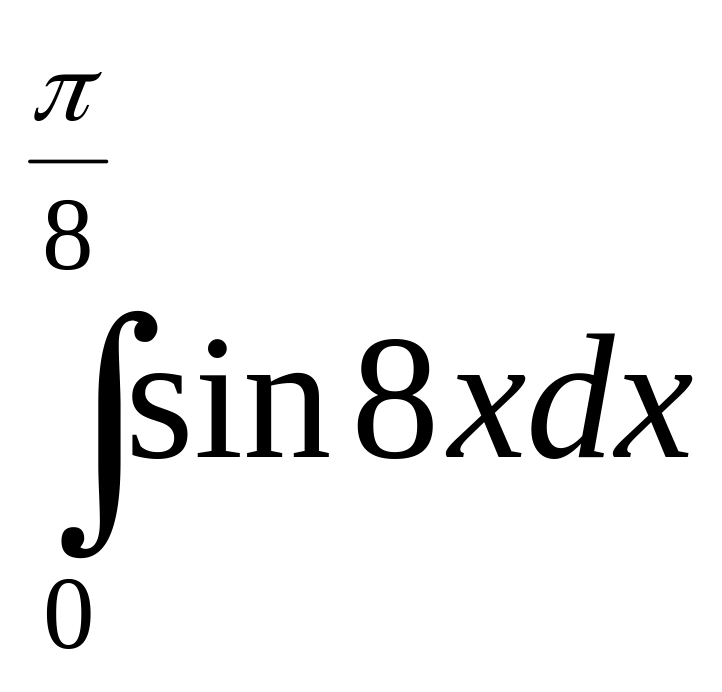
3.
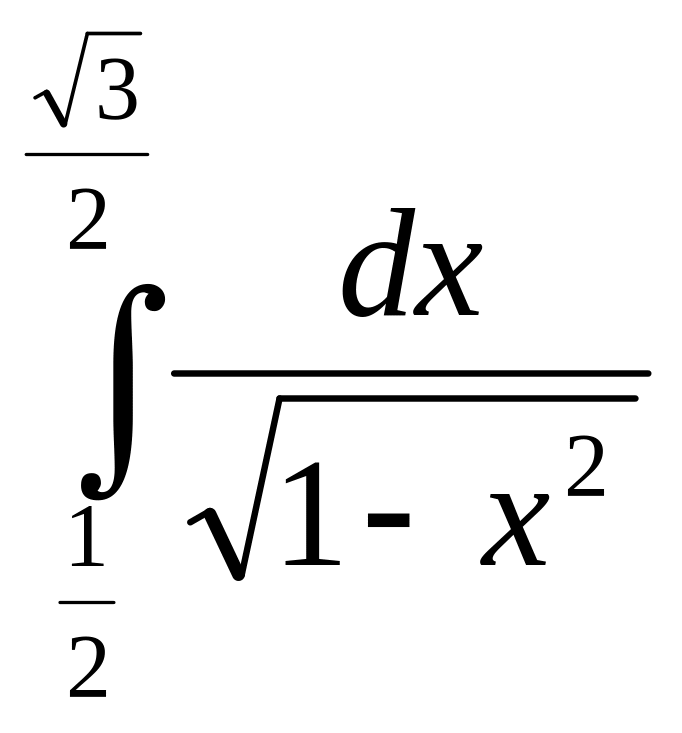 4.
4.
![]()
5.
![]() 6.
6.
![]()
Упражнения для самопроверки
7.
![]() 8.
8.
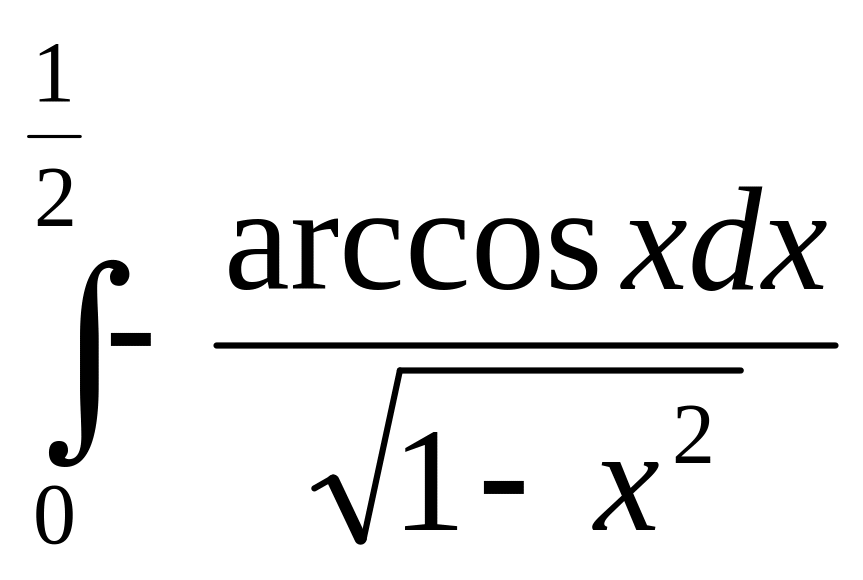
9.
![]() 10.
10.
![]()
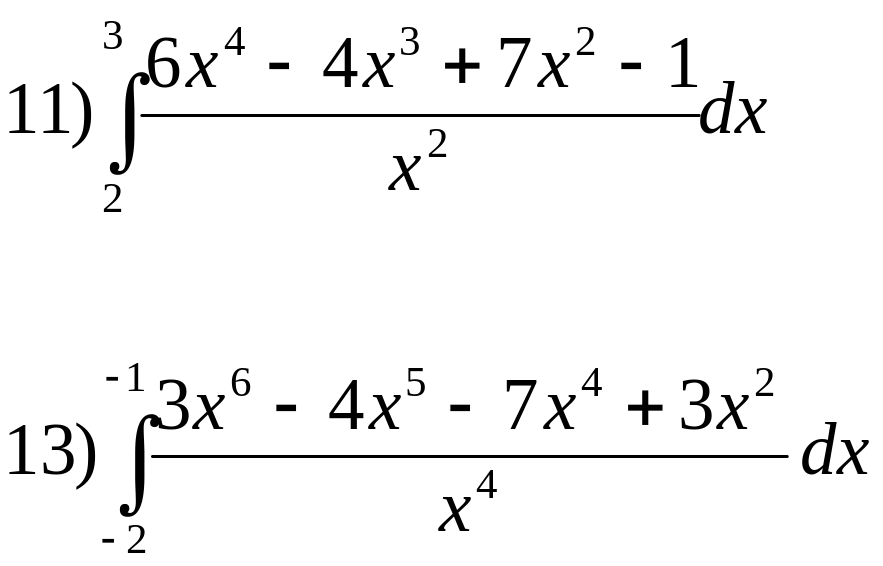
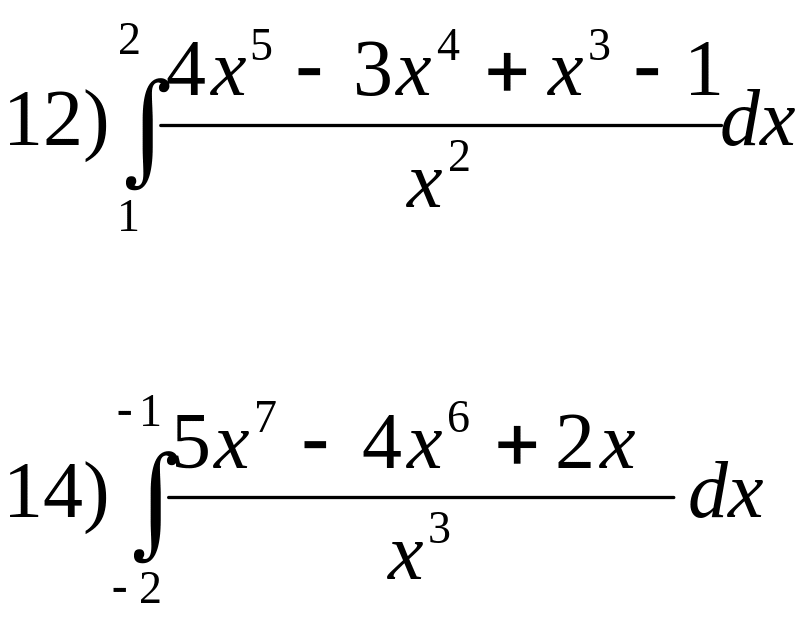
№ 4. Найти площадь фигуры, ограниченной графиками функций:
1) 2) 3) 4)
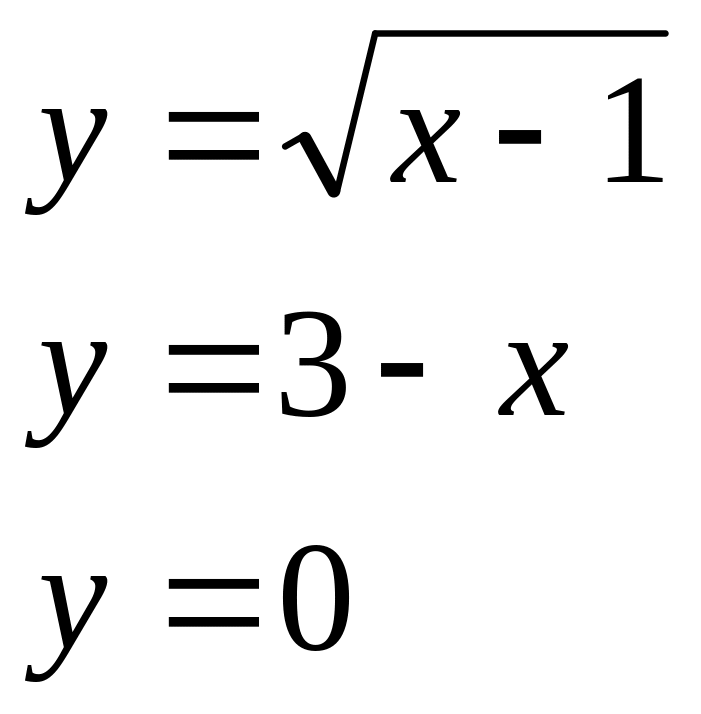
![]()
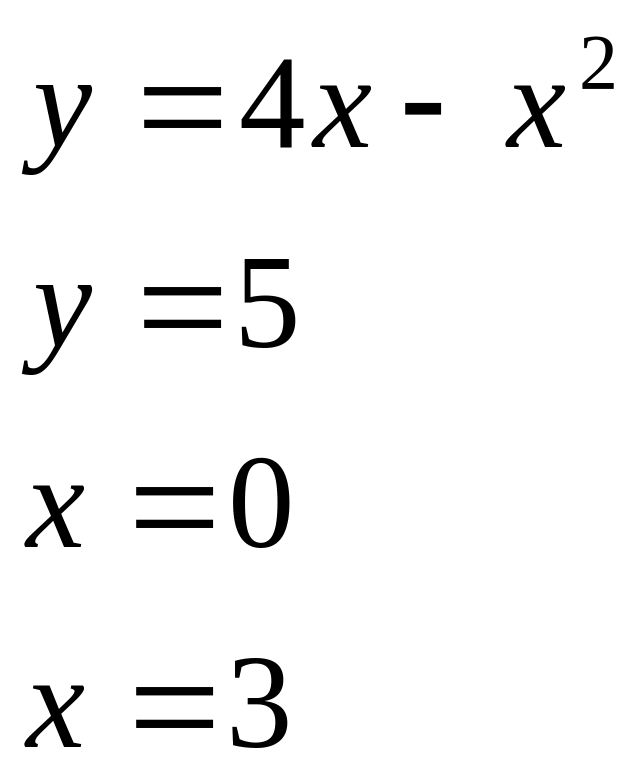
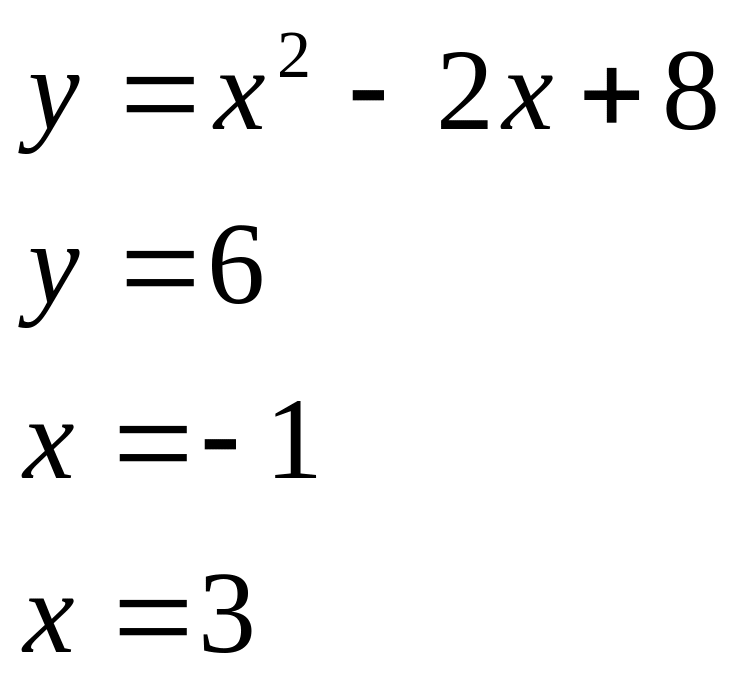
5) 6) 7) 8)