Л 4 «Интегралы»

Тема 1.3 Интегральное исчисление

Неопределенный интеграл

Основной задачей дифференциального исчисления является нахождение производной f(x) или дифференциала df= ḟ(x)dx функции f(x). В интегральном исчислении решается обратная задача. По заданной функции f(x) требуется найти такую функцию F(x),что F(x)=f(x) или dF(x)=F’(x)dx=f(x)dx.

Таким образом, основной задачей интегрального исчисления является восстановление функции F(x) по известной производной (дифференциалу) этой функции.

Определение 1. Дифференциалом функции называется произведение

производной этой функции на произвольное приращение аргумента:

, или

Определение 2. Функция F(x) называется первообразной для функции , если

Очевидно, что если F(x) – первообразная для , то и всякая функция вида , где С=const, также является первообразной для функции . Это утверждение в школьной математике носит имя «общий вид первообразных». Действительно, , поскольку производная константы равна нулю. Так как по условию - первообразная для , то по определению 2 : , следовательно, , и опять-таки по опр. 2 следует, что - первообразная для .

Определение 3. Совокупность всех первообразных для функции называется неопределенным интегралом от этой функции.

.

Таким образом,

Определение 4. Операцию нахождения неопределенного интеграла от функции будем называть интегрированием функции , а саму функцию - подынтегральной.

Эта операция сводится к отысканию такой функции , производная которой равно подынтегральной функции . Подспорьем к интегрированию является таблица интегралов от некоторых элементарных функций, приведенная ниже.

1. 11.

2. 12.

3. 13.

4. 14.

5. 15.

6. 16.

7. 17.

8. 18.

9. 19.

10. 20.

Каждая формула в этой таблице может быть легко перепроверена с помощью изученных ранее формул производных элементарных функций. Для этого достаточно вычислить производную от функций, стоящей в правой части формулы, и убедиться, что получилось подынтегральная функция. Рассмотрим, к примеру, интеграл от степенной функции:

В дальнейшем при интегрировании понадобятся также два очевидных свойства линейности интеграла:

1) (т.е. интеграл от суммы (разности) функций равен сумме (разности) интегралов от каждой из этих функций в отдельности);

2) (т.е. постоянный множитель можно выносить за знак интеграла).

Примеры:

1)

2)

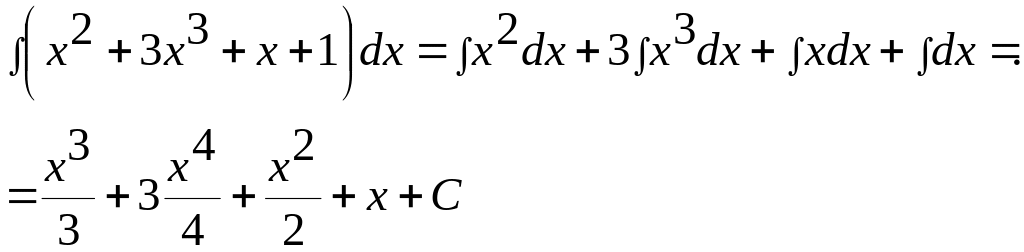
3 )

4)

5)

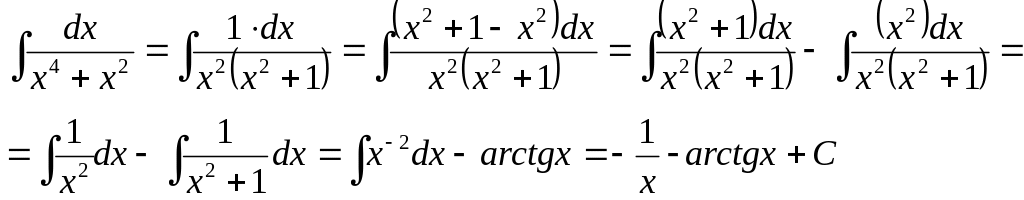
Замена переменной в неопределенном интеграле

Если функция f(x) непрерывна, а функция (t) имеет непрерывную производную (t), то имеет место формула

_ f((t))(t) dt = _ f(x) dx, где x = (t).

Можно привести примеры вычисления интеграла с помощью перехода от левой части к правой в этой формуле, а можно привести примеры обратного перехода.

Суть метода замены заключается в переходе от одной переменой, стоящей под знаком интеграла, к другой. При такой замене аргумента изменится также подынтегральный дифференциал аргумента. Весь фокус состоит в том, чтобы наперед разглядеть хотя бы в общих чертах подынтегральное выражение, которое получится в результате замены переменной, и убедиться, что новый интеграл «берется» без труда табличным способом! Только в этом случае замена переменной целесообразна.