2.Сызықтық функцияның қасиетерінің оның графигі арқылы сипатталуы.

Сызықтық функцияның қасиетерінің оның графигі арқылы сипатталады. Мәселен у=0,5х-2 функциясы қарастырылады:оның мәндерінің кестесі құрылады;координата жазықтығында осы кестеде берілген нүктелер салынады;сонда шыққан нүктелердің бір түзудің бойында жататындығы көрсетіледі.у=0,5-2 сызықтық ф.яның грфигі түзу сызық болатындығы туралы қортынды жасалады. Жалпы ұйғарым тужрымдалады:сызықтық функцияның графигі түзу сызық болып табылады.

3.Сызықтық функцияны графигін салуды оқушыларға қалай үйретіледі.

у=kx+l функциясының графигi түзу сызық. k0, l0 болған жагдайда, мұндай функцияның графигi координаталар жүйесiндегi абсцисса өсiн де, ордината өсiн де қияды. Графиктiң ордината өсiмен қиылысу нүктесiнiң координатасы (0;l) болады. Себебi у=kx+lфункциясында х=0 болғанда у=k0+l; y=l.Ал y=kx+lсызықтық функция графигiнiң абсцциссалар өсiмен қиылысу нүктесiнiң ординатасы у=0 болса, онда 0=kх+l; kх=-l; 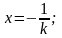Демек, у=kх+l функциясының графигi абсцисса өсiн 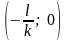нүктесiнде қияды. Сызықтық функцияның графигi түзу сызық болатындықтан, түзудiң бiрiншi нүктесi ретiнде (0;l) нүктесiн алып, екiншi нүктесiн табу үшiн х-ке қалаған қандай да бiр сан мәнiн берiп, оған сәйкес у-тi табамыз. Осылайша түзудi жүргiзу үшiн қажеттi екiншi нүктенiң координатасы табылады.

Мысалы, у=2х+3 функциясының графигiн салайық (1-сурет).

Х	0	-2
У	3	-1

1)у=kx+l сызықтық функцияның формуласындағы: l=0; k0 болса, у=kх функциясы тура пропорционалдық болады. Мұндағы х=0 болса, у=0. Демек, барлық у=kх түрiндегi функциялар графигiне ортақ нүкте О(0;0) нүктесi (координаталар басы). Осыдан шығатын қорытынды: у=kx тура пропорционалдығының графигi координаталар басынан (О(0;0) нүктесiнен) өтетiн түзу (2-сурет).2) Осы тұжырымнан кейiн, у=kx функциясының графигiн салу үшiн О(0;0) нүктесiнен басқа, екiншi бiр нүкте тауып, екi нүкте арқылы түзу жүргiзу жеткiлiктi екендiгiн айту керек. Екiншi нүкте x-қа кез келген мән берiп, у-тiң сәйкес мәнiн есептеу арқылы табылады. у=kx функциясының графигiн салуға бiрнеше жаттығу орындалады.Сонда оқушы у=kx функциясының графигiн салудың оқулық авторы ұсынғандай, у=kx+l функциясының графигiне байланысты ғана емес, оған тәуелсiз салуға дадағдыланады.у=kx тура пропорционалдығының графигi k>0 болғанда Iжәне IIIкоординаталық ширектерде жатса, k<0 болғанда IIжәне IVкоординаталық ширектерде жатады.2) Егер у=kx+l сызықтық функциясындағы k=0; l0 болса, берiлген функция у=l сызықтық функциясының графигi абсциссалар өсiне параллель және (0; l) нүктесi арқылы өтетiн түзу (3-сурет).у=kx+l функциясының графигiн пайдаланып, у=kx функциясының графигiн салу үшiн координаталар басы О(0;0) нүктесi арқылы у=kх+l түзуiне параллель түзу жүргiзу керек. О(0;0) нүктесi арқылы жүргiзiлген у=kх+l түзуiне параллель түзу у=kx функциясының графигi болады.

4.Сызықтық функцияны аналитикалық тәсілмен қалай зеріттеледі.

Графиктік тәсілді қолданып,оқушылар ф.яны зерттеуге байланысты белгілі бір білімдерге ие болады.Функцияны зерттеудің ең дәл тәсілі теңдеулер мен теңсіздіктерге,теңбе тең түрлендіруге негізделген аналитикалық тәсіл болып табылады.