
- •Математикалық өрнектер
- •Әріпті өрнектер
- •Санды өрнектер
- •10.1 Теңбе-теңдік және теңбе-тең түрлендіру ұғымымен оқушылар қай сыныптан бастап танысады?
- •10.2 Теңбе-теңдік және теңбе-тең түрлендіру ұғымы қай сыныптан бастап енгізіледі ?
- •10.6 Теңбе-тең түрлендіру кезінде мектеп оқушыларының жіберетін қателеріне мысалдар келтір
- •10.7 Теңбе-теңдік ұғымымен алғаш рет қалай таныстырады ?
- •11.1. Мектеп оқулықтарында функция ұғымын оқыту реті қандай?
- •11.2. Мектепте функция ұғымын нақтылы-индуктивтiк тәсiлмен енгiзу туралы айтып бер. Қандай функциялар осы тәсілмен енгізіледі?
- •11.3. Функция ұғымын абстрактілі-дедуктивтік тәсілмен енгізу сүлбесі қандай? Мектепте осы тәсілмен енгізілетін функциялар туралы айт.
- •11.4. Функция ұғымын енгізу мектеп оқулығында қалай баяндалады?
- •1.Сызықты функцияға келтиретін лайықты есепти қарастырайық.
- •2.Сызықтық функцияның қасиетерінің оның графигі арқылы сипатталуы.
- •3.Сызықтық функцияны графигін салуды оқушыларға қалай үйретіледі.
- •4.Сызықтық функцияны аналитикалық тәсілмен қалай зеріттеледі.
- •12.5 Мектепте квадрат функцияны оқыту реті қандай ?
- •13.1 Мектепте теңдеу ұғымына жүйелі түрде оқыту қайсы сыныптан басталады ?
- •13.2 Теңдеу дегеніміз не ?
- •13.3 Теңдеудің мүмкін мәндер облысы қалай табылады ?
- •13. 4. Теңдеудің түбірі деген не?
- •13,5. Теңдеуді шешудің жалпы әдістерін айтып бер?
- •13.6. Бастауыш сыныптарда теңдеулерді шешуге қалай үйретіледі?
- •14.2. Сызықтық теңдеуді шешу тақырыбын жүйелеу туралы айтып бер.
- •14.3 Екi белгісізі бар екі теңдеулер жүйесi ұғымы қалай енгізіледі?
- •14.5 Екі белгісізі бар екі сызықтық теңдеулер жүйесін шешудің қандай әдістері бар? Мысалдар арқылы түсіндіруді көрсет.
- •15.1 Мәтіндік есептер шешудің қандай маңызы бар?
- •15.2 Мәтiндiк есептердi арифметикалық тәсілмен шығарудың мәні неде?
Математикалық теңбе-тең түрлендірулер жасауға неге үйретіледі?
Теңбе-тең түрлендiрулер мектеп математика курсындағы ең басты мазмұнды-әдiстемелiк бағыттардың бiрi болып табылады. Әдетте, әрбiр математикалық есептi аналитикалық тәсiлмен шығару қандай да бiр теңбе-тең түрлендiрудi орындауды қажет етедi. Теңбе-тең түрлендiрулер алгебра мен математикалық анализ курсы бастамаларының өн бойында оқытылады.
Математикалық өрнектерді теңбе-тең түрлендіру мәдениетін қалыптастыру орта мектептегі ең өзекті мәселелердің бірі. Оқушы математикалық өрнектерді дұрыс түрлендірулер жүргізу нәтижесінде аналитикалық өрнекті қарапайым өрнекке келтіру, теңбе-теңдікті түрлендірулер тізбегіндегі өрнектің анықталу облысының өзгеруіне бақылау жасау, түрлендіруді жылдам және қатесіз орындау т.б. біліктіліктерді меңгереді.
Оқушылардың теңбе-тең түрлендіруді орындай алу мәдениеті математикалық объектілерге (сандарға, бірмүшеліктерге, көпмүшеліктерге, векторларға және т.с.с.) амалдар қолданудың қасиеттері және оларды орындау алгоритмі туралы білімдер негізінде дамиды. Теңбе-тең түрлендірулер жасай білмей математикада қадам жасау мүмкін емес.
Алгебра курсында теңбе-тең түрлендіру деп бір аналитикалық өрнекті онымен тең, формасы жағынан өзгеше басқа өрнекпен алмастыру түсініледі.Математикалық өрнектерді теңбе-тең түрлендірудің негізгі ұғымы «өрнек», «теңбе-теңдік».
Теңбе-тең түрлендіру деген қалай түсіндіріледі?
Теңбе-теңдік және теңбе-тең түрлендіру ұғымы негізінен мектеп математика курсының 6-сыныбынан бастап енгізіледі. Бірақ сандық өрнектерді қарапайым түрлендірумен оқушылар бастауыш сыныптан бастап таныс. Бірінші сыныптың өзінде 5 және 2 сандарының қосындысын айқын немесе айқын емес түрде теңбе-тең түрлендіру жолымен былай табады: 5+2=5+(1+1)=(5+1)+1=6+1=7
Бастауыш сынып математикасында арифметикалық амалдарды орындау барлық жағдайда сандық түрлендірулер жасауды қажет етеді. Арифметикалық амалдардың қасиеттері әріптік теңбе-теңдік түрінде жазылады. Олар мынандай теңбе-теңдіктер:а+в = в+а; ав=ва; (а+в)с= ас+св.
Бұл келтірілген арифметикалық амалдардың заңдары бастауышта теңбе-теңдік деп аталмайды, бірақ олар сандық өрнектердің мәнін есептеу үшін кең түрде қолданылады. Оқушылар мұғалімнің көмегімен оларды саналы түрде қабылдап және өздігінен қолдана алуы тиіс.
6-сыныпта теңбе-теңдік ұғымы былай түсіндіріледі: Әріптік өрнектер теңбе-теңдік деп аталады, егер өрнекке енетін әріптердің әрбір сәйкес мәнінде теңдіктің оң және сол жақ бөліктері тең болса. Теңбе-тең түрлендіру жасағанда арифметикалық амалдарды орындап және олардың қасиеттерін қолданып жаңа өрнек аламыз, алынған жаңа өрнек бастапқы өрнекке теңбе-тең болады.
Мысалы:
 ,
,
 .
.
Мұғалім өз қалауынша теңбе-теңдік ұғымын басқаша да түсіндіруі мүмкін. Мысалы, алдымен екі өрнектің теңдігі ұғымын анықтасақ: «екі өрнек өзара тең деп аталады, егер олардың сәйкес мәндері тең болса». Одан кейін теңдік арқылы теңбе-теңдік ұғымының анықтамасын тұжырымдауға болады. «Теңдіктің сол жақ және оң жақ бөліктері өзара тең болса, онда ол теңбе-теңдік деп аталады». Енді ең бастысы теңбе-тең түрлендіруге анықтама берейік: «Өрнекті оған теңбе-тең басқа өрнекпен ауыстыру теңбе-тең түрлендіру деп аталады».Жоғары сыныптарда теңбе-теңдік және теңбе-тең түрлендіру ұғымдарына басқаша анықтама беріледі: Теңбе-теңдік деп оған енетін әріптердің барлық мүмкін мәндерінде дұрыс болатын теңдікті айтады. Әріптердің мүмкін мәндер жиынында бір өрнекті оған теңбе-тең өрнекпен ауыстыру теңбе-тең түрлендіру деп аталады.
Математикалық өрнек деп нені айтады?
Құрамында әріптері бар өрнек әріпті өрнек деп аталады.Мысалы: Санды өрнектер : 15-6, 45 -25 =20, 6 мұндағы 20 санды өрнектің мәні. 23 + а - әріпті өрнек, ал а=3 болғандағы 23+3=26. 26 саны әріпті өрнектің мәні .Санды өрнектер мен әріпті өрнектер - математикалық өрнектер. Математикалық өрнектер цифрлармен, амал таңбаларымен, әріптермен жазылады. Математикалық өрнектер қажет болған жағдайда жақшамен де жазылады. Математикалық өрнектерді жазуда латын әріптері пайдаланылады. Математикалық өрнектер белгілі бір шарттармен жазылады. Мысалы, өрнектегі көбейткіштер әріптермен беріліп, олар қатар келсе, араларына көбейту таңбасы салынбайды., ал сан көбейткіш жақшаның артында келсе, жақша мен сан көбейткіш арасына көбейту таңбасы қойылады. Математикалық өрнектер мәндері бойынша салыстырылады, Егер салыстыруда қос теңсіздік пайдаланылса, қос теңсіздік солдан оңға қарай өсу ретімен жазылады. Мысалы, 7<10<15; а<в+с<20.

Математикалық өрнектер
Әріпті өрнектер
Санды өрнектер
23
+ а; 86+(36+2в)

15
– 6; 7+33:3 17+(29+31);
140: (63+7)

Санды өрнектер мен әріпті өрнектер- математикалық өрнектер.
Мысалы: Санды өрнектер:, мұндағы 15-9=6; 6- санды өрнектің мәні.
а=3 23+3=26- әріпті өрнек, 26- саны әріпті өрнектің мәні
7а+3 – әріпті өрнегіндегі 7 саны коэффициент деп аталады.
Рационал, иррационал өрнектерге мысал келтір
Құрамындағы айнымаласы бөлімінде кездесетін бөлшектері бар өрнектер рационал өрнектер деп аталады. Бүтін өрнектерді көпмүше түріне келтіруге болады, олардың құрамындағы әріптердің кез келген мәндерінде мағыналары бар. Себебі қосу мен көбейтудің және дәрежеге шығару амалдарының айнымалының кез келген мәнінде мағынасы бар. Ал бөлшек өрнектердің айнымалылардың кейбір мәндерінде мағынасы болмауы мүмкін. Мысалы, a+ ( 1)/( a) өрнегінің a=0 болғанда мағынасы жоқ. a/b түрінде берілген өрнекті рационал бөлшек деп атайды. Мұнда a мен b- рационал өрнектер, b-нің құрамында айнымалылар бар. Мысалы, 2x/(x²-5); (3y+1)/7y
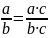 теңбе
- теңдігі бөлшектің негізгі қасиеті.
Осы теңбе-теңдікті
пайдаланып,
теңбе
- теңдігі бөлшектің негізгі қасиеті.
Осы теңбе-теңдікті
пайдаланып,
 бөлшегін с
көбейткішіне
қысқартуымызға болады.
бөлшегін с
көбейткішіне
қысқартуымызға болады.
 =
=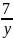
 бөлшегін
қысқарту үшін өрнектерді оған теңбе
тең өрнектермен алмастырып алу қажет.
бөлшегін
қысқарту үшін өрнектерді оған теңбе
тең өрнектермен алмастырып алу қажет.


Егер
берілген алгебралық өрнектерде төрт
арифметикалық амалдар және дәрежеге
көтеру мен бірге түбір шығару амалы да
қатысса, мұндай өрнектерді иррационал
өрнектер деп аталады. Мысалы:

Анықтама:
Теріс емес а санның n–дәрежені
арифметикалық түбірі деп n–дәрежесі а
санына тең болатын теріс емес санға
айтылады да оны
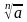 деп белгіленеді.Сөйтіп,
деп белгіленеді.Сөйтіп,
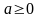 болғанда
болғанда
 болып,
болып,
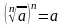 болады екен.Осы анықтамадан дербес
жағдайда (n=2)
болады екен.Осы анықтамадан дербес
жағдайда (n=2)
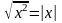 теңдік келіп шығады.
теңдік келіп шығады.
1.
 теңдік орындалады.
теңдік орындалады.
 Иррационал
өрнектерді түрлендіруде мына теңдіктерден
де пайдалануға болады:
Иррационал
өрнектерді түрлендіруде мына теңдіктерден
де пайдалануға болады:
2.
 3.
3.
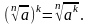 4.
4.
 5.
5.

Мысал.
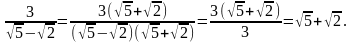
Қандай өрнектер бүтін, бөлшек делінеді?
Біз
құрамында айнымалылары бар өрнектерді
қарастырдық , бұл өрнектер бүтін
өрнектер
деп аталады. Ал, құрамындағы айнымаласы
бөлімінде кездесетін бөлшектері бар
өрнектер рационал
өрнектер
деп аталады.Мысалы:
![]()
Бүтін
өрнектерді көпмүше түріне келтіруге
болады, олардың құрамындағы әріптердің
кез келген мәндерінде мағыналары бар.
Себебі қосу мен көбейтудің және дәрежеге
шығару амалдарының айнымалының кез
келген мәнінде мағынасы бар. Ал бөлшек
өрнектердің айнымалылардың кейбір
мәндерінде мағынасы болмауы мүмкін.
Мысалы, a+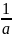 өрнегінің a=0 болғанда мағынасы жоқ.
өрнегінің a=0 болғанда мағынасы жоқ.
![]() - мұндай, құрамында айнымалысы
бөлімінде кездесетін бөлшектері бар
өрнектер бөлшек
өрнектер
деп аталады. Жалпы алғанда бүтін және
бөлшек өрнектерді рационал
өрнектер деп
атайды.
- мұндай, құрамында айнымалысы
бөлімінде кездесетін бөлшектері бар
өрнектер бөлшек
өрнектер
деп аталады. Жалпы алғанда бүтін және
бөлшек өрнектерді рационал
өрнектер деп
атайды.
10.1 Теңбе-теңдік және теңбе-тең түрлендіру ұғымымен оқушылар қай сыныптан бастап танысады?
Жаңа бағдарламаға сәйкес оқушылар теңбе-теңдiк ұғымымен алғаш рет 5-сыныпта танысады.
Алдымен әрiптi өрнек ұғымы айтылғаннан кейiн‚ әрiптi өрнектердi жазуда төмендегiдей ережелер мен шарттарды ескеру қажеттiгi айтылады:
1.
Егер екi көбейткiштiң бiреуi сан болса,
ол коэффициент деп аталып, ол әрiп
көбейткiштiң алдына жазылады. Коэффициент
пен әрiп көбейткiштiң арасына көбейту
()
таңбасын қоймауға да болады. Мысалы,
7х;
3у;
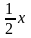 ;
0,7у.
;
0,7у.
2. Әрiптi өрнектегi әрiп көбейткiштерiнiң арасына көбейту таңбасы қойылмайды. Мысалы, mn; 0,3ху;
3.
Құрамында әрiптерi бар бөлiндi, бөлшек
түрiнде жазылады. Мысалы,
 .
.
4. Әрiптi өрнектегi амалдардың орындалуы кезiнде жақшаның алатын орны ерекше. Мысалы, 9-(a+b) өрнегi мен 9-а+b өрнегi бiрдей емес.
Өрнек
бөлшекпен берiлген жағдайда, санды нөлге
бөлуге болмайтындықтан, өрнектiң мағынасы
болуы үшiн бөлшектiң бөлiмi нөлге тең
болмауы шарт. Осы шарттың орындалуынан
келiп, әрiптi өрнектегi әрiптердiң сан
мәндерi ұғымы қалыптасады. Өрнектегi
әрiптердiң сан мәндерi өзгерiп отыратындықтан,
ондағы әрiптi айнымалы деп, әрпi бар
өрнектi айнымалысы бар өрнек деп атайды.
Мысалы.
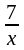 ,
өрнегiндегi х-тiң
қабылдайтын мәндерi 0 санынан басқа
барлық сандар;
,
өрнегiндегi х-тiң
қабылдайтын мәндерi 0 санынан басқа
барлық сандар;
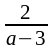 өрнегi а
үшiн а=3
санынан басқа барлық сандарды қабылдайды.
өрнегi а
үшiн а=3
санынан басқа барлық сандарды қабылдайды.
