
- •Методические указания и задания к контрольным работам студентов
- •II курса заочного отделения
- •Контрольная работа № 7 для зрф
- •Кратные интегралы»
- •Примеры решения контрольных заданий
- •Задания к контрольной работе № 7 для зрф
- •Варианты контрольных заданий
- •Контрольная работа № 8 для зрф
- •Примеры
- •Варианты контрольной работы
- •Контрольная работа № 9 для зрф Тема: «Элементы теории поля»
- •Задания к контрольной работе № 9 для зрф
- •Примеры для решения контрольной работы № 10
- •Задания к контрольной работе № 10 для зрф
- •Литература
Примеры для решения контрольной работы № 10
Контрольная работа содержит 5 контрольных заданий.
Дадим 2 примера контрольного задания №1.
Пример 1: Исследовать сходимость числового
ряда
![]()
Решение. Применим признак сравнения 1.4.1.4)
 .
Возьмем
.
Возьмем
![]() ,
тогда
,
тогда
![]() .
Рассмотрим ряд
.
Рассмотрим ряд
![]() .
Применим интегральный признак 1.4.2)
.
Применим интегральный признак 1.4.2)
![]() ,
,
![]() –
монотонно убывает.
–
монотонно убывает.
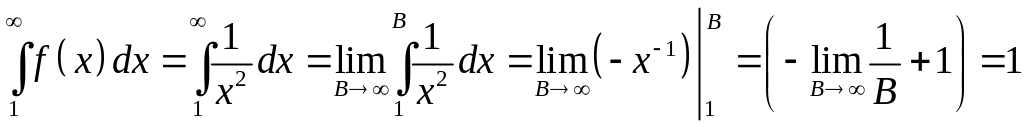 .
Интеграл сходится, следовательно по
1.4.2), ряд
.
Интеграл сходится, следовательно по
1.4.2), ряд
![]() сходится,
а, значит,
ряд
сходится по 1.4.1.4)
сходится,
а, значит,
ряд
сходится по 1.4.1.4)
Пример 2. Исследовать сходимость числового
ряда
![]() .
.
Решение. Применим признак Даламбера
1.7)
![]() ;
;
![]() .
.
По определению
![]() ;
;
![]() ;
;
![]() .
.
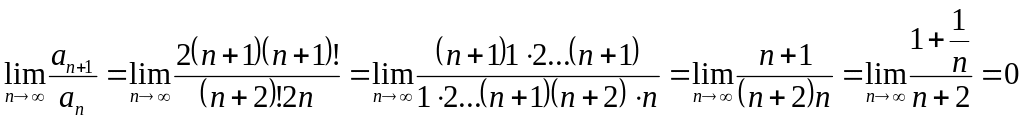
q = 0, q < 1 следовательно, ряд сходится.
Пример контрольного задания № 2.
Найти интервал сходимости степенного
ряда
![]() ;
;
![]()
Решение. Применим план нахождения интервала сходимости 2.3)
Составим ряд из абсолютных величин членов ряда
![]() ,
,
![]() .
.
Применим признак Даламбера к полученному ряду
![]() ,
,
![]() .
.
Ряд сходится при
![]() ,
т.е.
,
т.е.
![]() ,
или
,
или
![]() .
Радиус сходимости
.
Радиус сходимости
![]() .
.
Исследуем сходимость числового ряда на границах интервала при
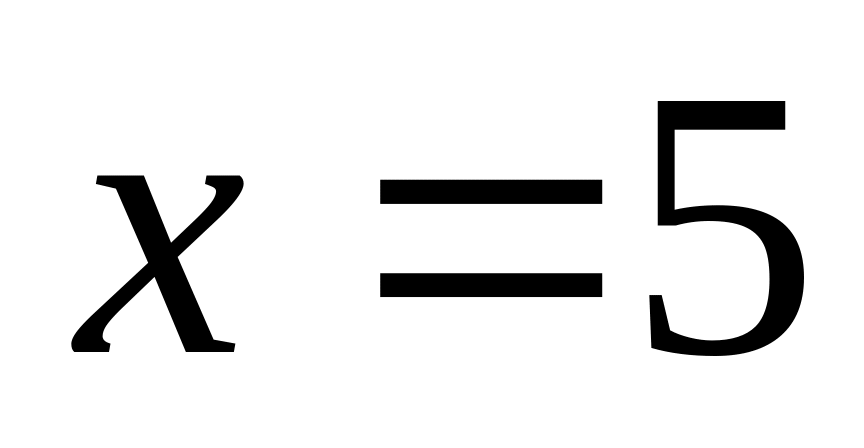 и
и
 .
.
а)
Получим числовой ряд
![]() .
Общий член этого ряда
.
Общий член этого ряда
![]() .
Применим необходимый признак сходимости
1.3.1).
.
Применим необходимый признак сходимости
1.3.1).
![]()
ряд
ряд
![]() расходится.
расходится.
б)
.
Получим числовой ряд
![]() .
Это знакочередующийся ряд. Абсолютная
величина общего члена ряда
.
Это знакочередующийся ряд. Абсолютная
величина общего члена ряда
![]() .
По необходимому признаку сходимости
1.3.1) ряд
.
По необходимому признаку сходимости
1.3.1) ряд
![]() расходится.
расходится.
Итак, на границах интервала исходный ряд расходится.
Вывод. Интервал сходимости степенного ряда .
Пример контрольного задания № 3.
Вычислить определенный интеграл
![]() ,
,
![]() ,
с точностью до 0,001, разложив подынтегральную
функцию в степенной ряд и проинтегрировав
почленно.
,
с точностью до 0,001, разложив подынтегральную
функцию в степенной ряд и проинтегрировав
почленно.
Решение: Разложим
![]() в ряд по таблице 3.2) для
в ряд по таблице 3.2) для
![]() .
.
![]()
![]() ;
;
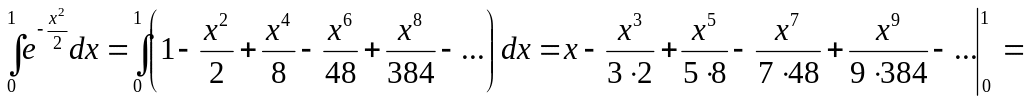
![]()
Мы получили знакочередующийся ряд. Если
ограничиться четырьмя членами, то по
следствию 1.5.2) из признака Лейбница
остаток ряда
![]() ,
т.е. точность
,
т.е. точность
![]() .
.
Итак,
![]() с точностью
с точностью
![]() .
.
Пример контрольного задания № 4.
Найти три первых, отличных от нуля члена
разложения в степенной ряд решения
![]() дифференциального уравнения
,
удовлетворяющего начальному условию
дифференциального уравнения
,
удовлетворяющего начальному условию
![]() .
.
![]()
![]()
Ищем решение в виде ряда Маклорена в
окрестности
![]()
![]() Продифференцируем уравнение несколько
раз подряд, рассматривая у как
функцию от х.
Продифференцируем уравнение несколько
раз подряд, рассматривая у как
функцию от х.
![]() ,
,
![]() и
т.д. Возьмем в самом уравнении и
во всех равенствах
и
т.д. Возьмем в самом уравнении и
во всех равенствах
![]() и
принимая во внимание
,
найдем
и
принимая во внимание
,
найдем
![]() ,
,
![]() ,
,
![]() ,
подставив эти коэффициенты в ряд
Маклорена, получим решение
,
подставив эти коэффициенты в ряд
Маклорена, получим решение
![]()
Пример контрольного задания № 5.
Разложить
![]() в ряд Фурье в интервале
в ряд Фурье в интервале
![]() .
.
![]() ;
;
 ;
;

 ;
;
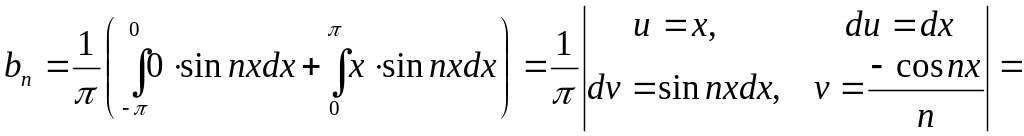
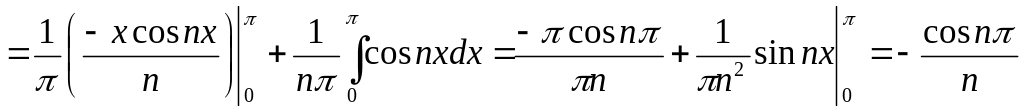 .
.
Тогда
![]() .
.
Задания к контрольной работе № 10 для зрф
Исследовать сходимость числового ряда
 .
.Найти интервал сходимости степенного ряда
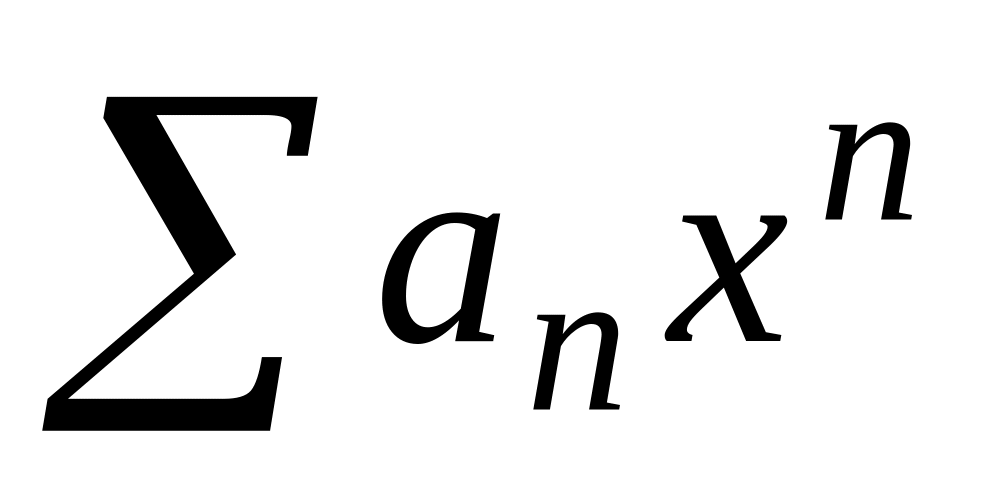 .
.Вычислить определенный интеграл , с точностью до 0,001, разложив подынтегральную функцию в степенной ряд, а затем проинтегрировав его почленно.
Найти три первых, отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения , удовлетворяющего начальному условию .
Разложить данную функцию в ряд Фурье в интервале
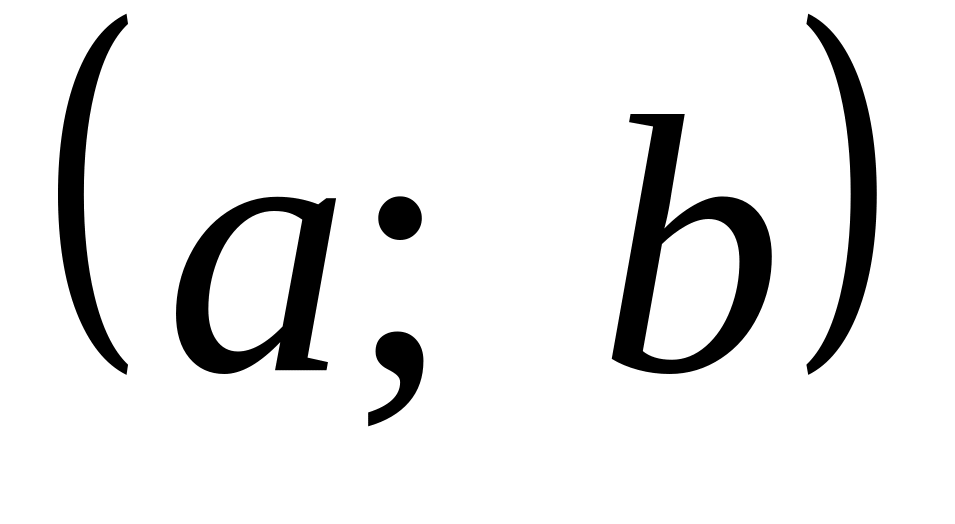 .
.
№ вар-та |
Задания |
1 |
1)
|
2 |
1)
|
3 |
1)
|
4 |
1)
|
5 |
1)
|
6 |
1)
|
7 |
1)
|
8 |
1)
|
9 |
1)
|
10 |
1)
|
