Контрольная работа № 9 для зрф Тема: «Элементы теории поля»

Краткая теория и методические указания

к выполнению контрольных заданий

1. Скалярное поле, градиент, производная по направлению.

Задана функция в области D (задано скалярное поле в области D) и точка в области D.

1. Градиентом функции называется вектор 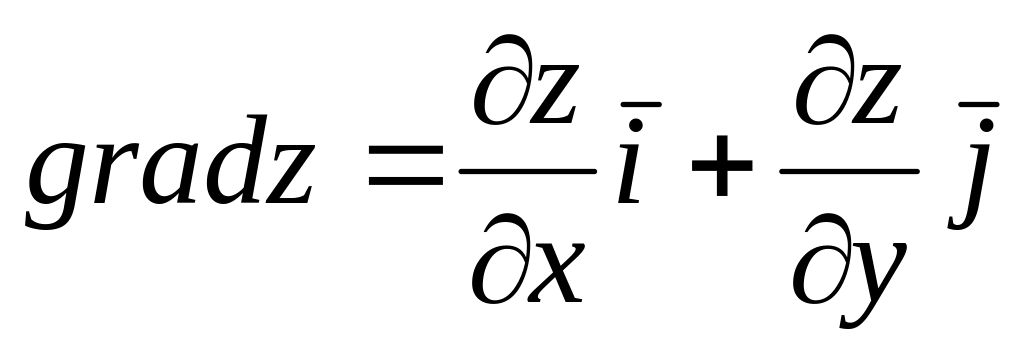; – частные производные функции z по x и по y. Направление вектора градиента в точке – это направление наискорейшего возрастания поля в этой точке, а модуль вектора градиента – величина максимальной скорости возрастания. Модуль (длина) градиента . Направляющие косинусы градиента , , 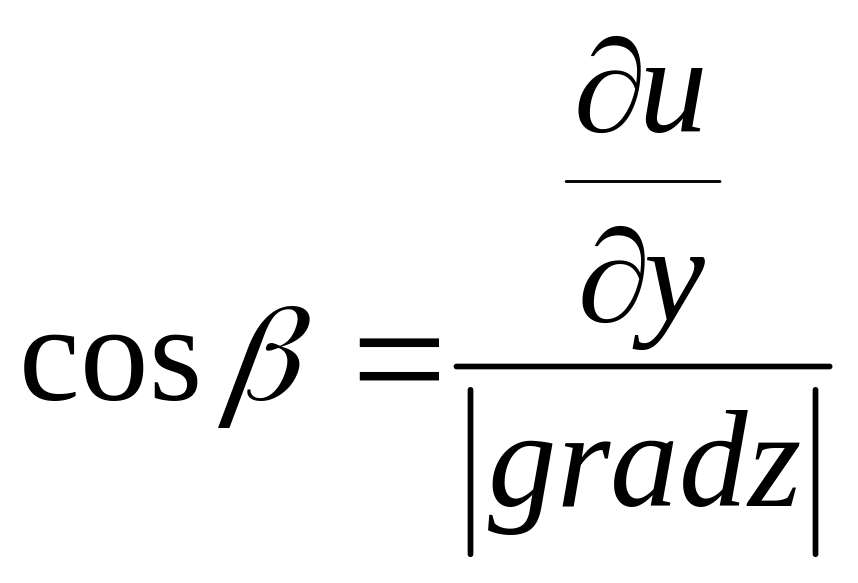где и – углы вектора с осями х и у.

2. Производная от функции в точке по направлению вектора вычисляется по формуле 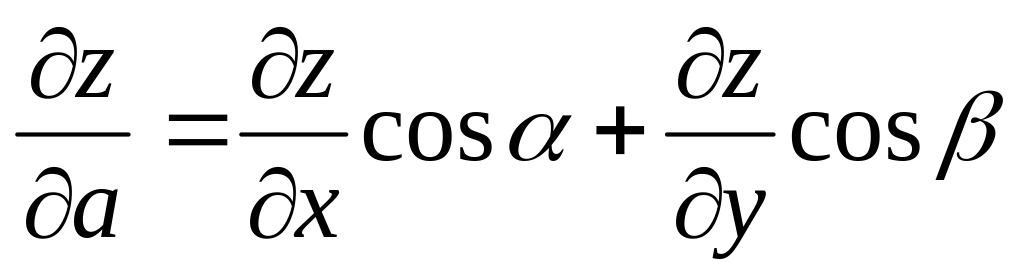, где – значения частных производных в точке А; 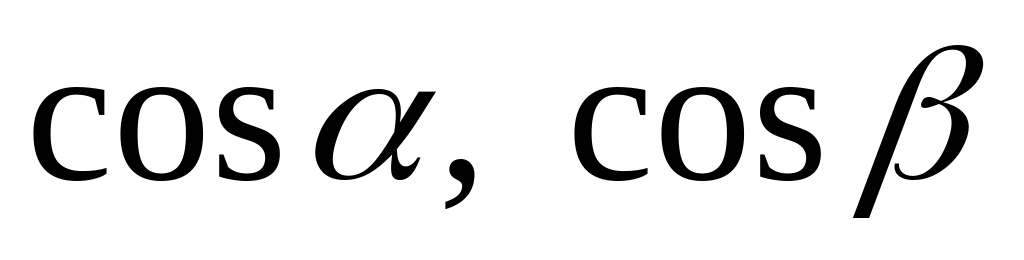– направляющие косинусы вектора . Модуль вектора 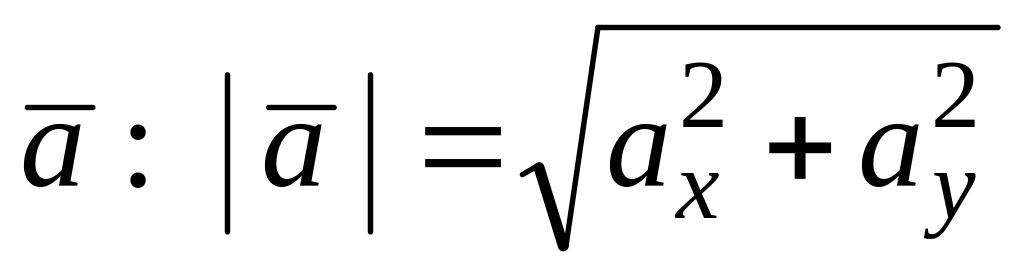. Значение – это скорость изменения поля в направлении вектора , если > 0, то поле возрастает, если < 0, то поле убывает.

2) Криволинейные интегралы вдоль кривой от точки до точки .

2.1) Криволинейный интеграл по длине дуги (I рода) применяется, в частности, для

вычисления массы или заряда, распределенных по кривой с плотностью

2.2) Криволинейный интеграл по координатам (II рода) применяется, в частности, для

расчета работы силового поля при перемещении мате-

риальной точки по кривой

2.3) Вычисление криволинейных интегралов сводится к вычислению определенных ин-

теграллов.

Дифференциал длины дуги ;

2.3.1) Пусть кривая задана параметрически

Тогда ,

,

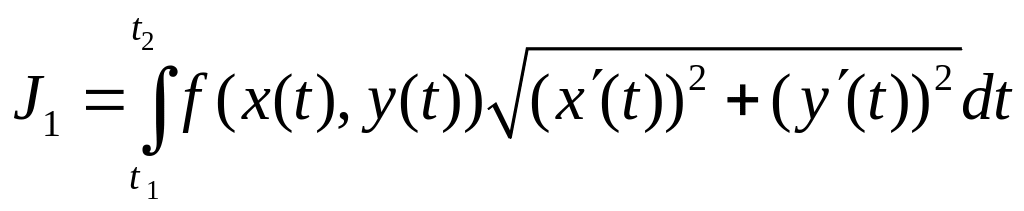
где и - значения параметра, соответствующие точкам и линии .

2.3.2) Пусть уравнение линии задано .

Тогда .

,

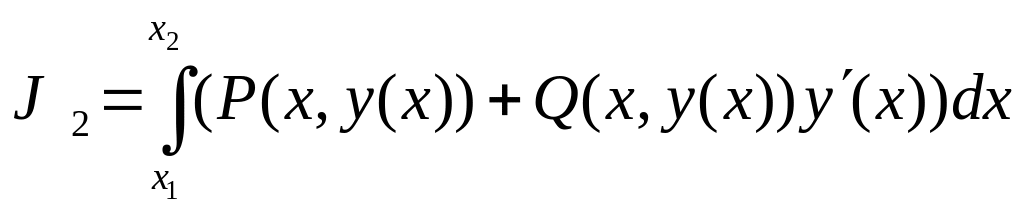где и - абсциссы точек и линии .

2.3.3) Криволинейный интеграл по координатам

можно записать в виде криволинейного интеграла по длине дуги, так как

, , где и - косинусы углов вектора, касательно-

го к линии , соответственно с осью и осью (направляющие косинусы).

2.3.4) Криволинейные интегралы от функции 3-х переменных по пространственной линии.

Тогда - плотность массы (заряда) и вектор силового поля

являются функциями трех переменных .

Вычисление криволинейных интегралов сводится к вычислению определенных интег-

ралов.

Если кривая задана параметрическими уравнениями: 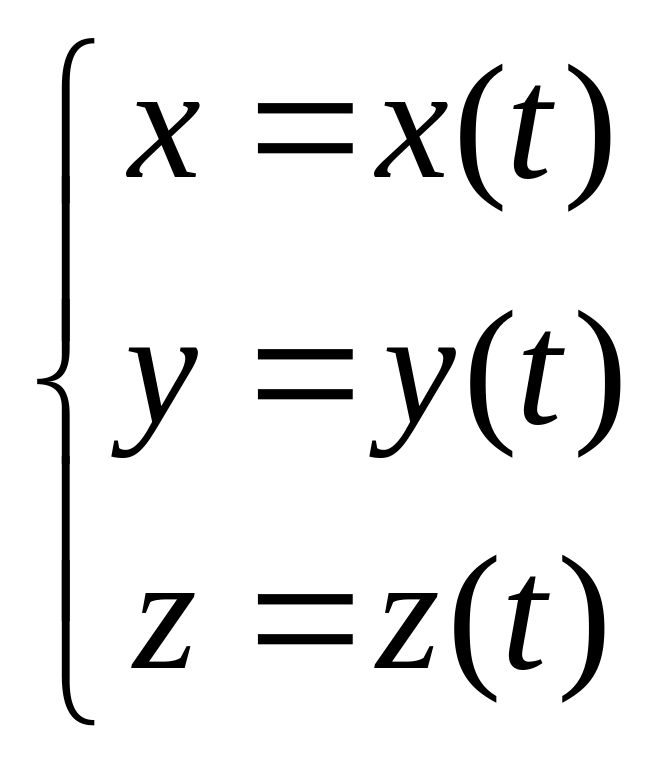, то

, ,

,

где и значения параметра , соответствующее начальной и конечной точ-

кам кривой .

3. Поверхностные интегралы.

3.1. Поверхностный интеграл по площади (I рода).

Применяется, в частности, для вычисления суммарных массы или заряда, распреде-

ленных по поверхности с плотностью .

- дифференциал площади поверхности .

3.2. Поверхностный интеграл по выбранной стороне поверхности ( рода)

Применяется, в частности, для вычисления потока жидкости через поверхность ,

если скорость потока

, где - единичный вектор нормали к поверхности ,

, - углы нормали к поверхности с осями

соответственно.

3.3. Вычисление поверхностных интегралов сводится к вычислению двойных интегралов

3.3.1 Если поверхность можно записать в виде , - проекция поверхнос-

ти на плоскость , то или .

Если поверхность можно записать в виде , - проекция поверхнос-

ти на плоскость , то или .

Если поверхность можно записать в виде , - проекция поверх-

ности на плоскость , то или .

Тогда можно вычислить с помощью двойных интегралов.

или

или

Для вычисления поверхностного интеграла рода углы считаются

острыми.

3.3.2 При вычислении поверхностных интегралов II рода различают стороны поверхно-

сти в зависимости от направления нормали к поверхности; , , -

направляющие косинусы нормали, проведенной к той стороне поверхности, по

которой проводится интегрирование

;

Можно записать так:

Обычно вычисление сводится к вычислению суммы двойных интегралов

Обозначение « » означает, что берем знак «+», если нормаль к поверхности

образует острый угол с соответствующей осью, знак «-», если угол больше

( для - с оью , для - с осью , для - с осью ).

4)Элементы векторного анализа.

Даны: векторное поле , поверхность и замкнутый контур .

4.1) Поток вектора через поверхность в направлении нормали к поверхности есть поверхностный интеграл

4.1.1) , где – углы нормали с осями . Поверхностный интеграл сводится к вычислению двойных интегралов по областям – проекциям поверхности на плоскости .

4.1.2) . « » означает, что знак «+», если нормаль к образует острый угол с соответствующей осью, знак «–», если угол больше 90º ( - с осью х, - с осью у, - с осью z).

4.2) Циркуляция векторного поля по замкнутому контуру – это криволинейный интеграл.

4.2.1) . Он вычисляется по правилу 2).

4.2.2) Ротор векторного поля, характеризующий завихрение его силовых линий, вычисляется с помощью определителя: .

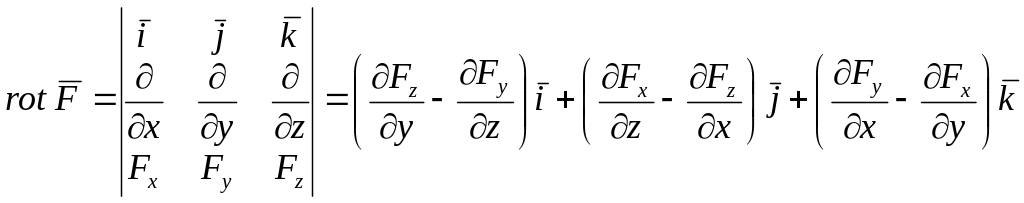4.2.3) Формула Стокса. Поток ротора векторного поля через поверхность равен циркуляции вектора по границе этой поверхности. .

.

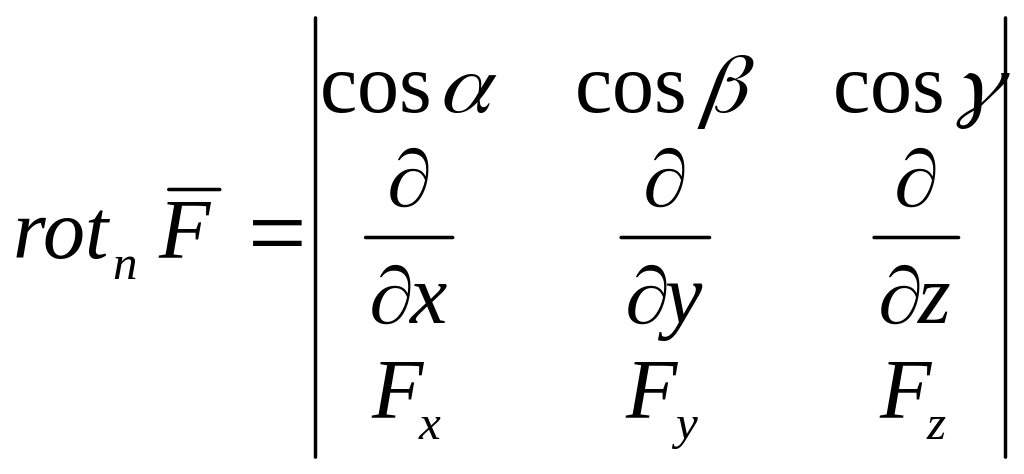Направление обхода контура и направление нормали к поверхности должны быть согласованы так – если идти по контуру в направлении интегрирования так, что область внутри контура остается слева, то направление от ног к голове совпадет с направлением нормали.

4.3) Дивергенция (расходимость) поля есть .

4.3.1) Теорема Гаусса-Остроградского. Поток вектора изнутри замкнутой поверхности равен тройному интегралу от дивергенции поля по объёму, ограниченному этой поверхностью.

4.3.2) .

5)Соленоидальное и потенциальное поля.

Дано векторное поле .

5.1) Если , то поле называется соленоидальным (трубчатым).

5.2) Если , то поле называется потенциальным.

Тогда , - полный дифференциал скалярного поля . Потенциал , (5.3)

г

M

M₀

x

z

y

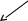
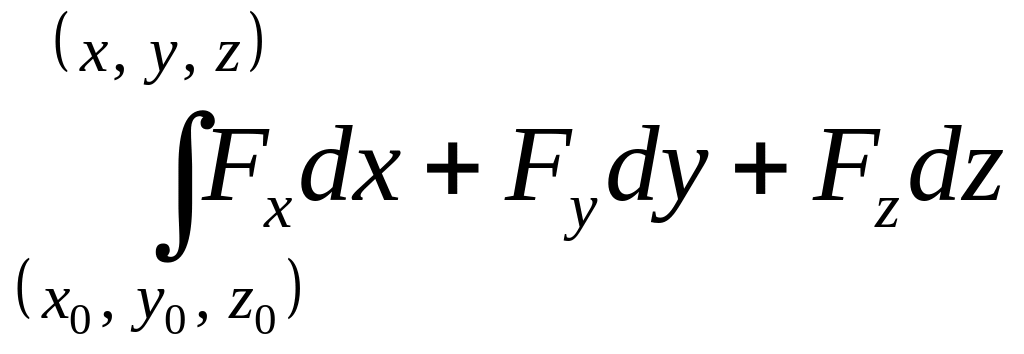де – фиксированная точка в рассматриваемой области. Формула (5.3) получается в результате вычисления интеграла по ломаной (рис. 1), звенья которой параллельны осям координат.

M₂

M₁

Примеры к решению контрольных заданий

Пример 1: Дана функция , вектор и точка .

1. Найдем градиент в точке . Воспользуемся 1.1)

; ; . Значения и в точке А получим, подставив координаты точки А. ; .

, т.е. ; направляющие косинусы градиента ; .

2. Найдём производную в точке А по направлению вектора . Пользуемся 1.2)

, где и – это направляющие косинусы вектора . ; ; ;

Вывод: По направлению вектора возрастает со скоростью 7,24 (меньше, чем по направлению градиента.

Пример 2.

Дана кривая .

1. Вычислить массу отрезка кривой от точки 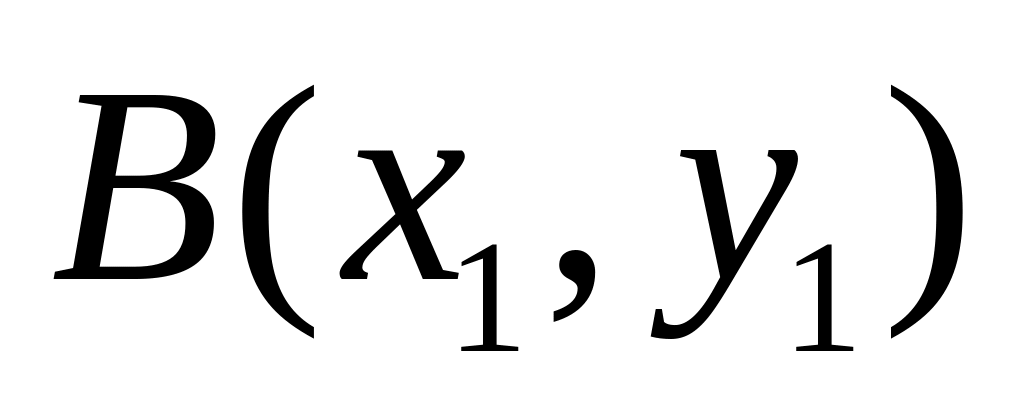до точки , если зада-

на плотность . .

2. Вычислить работу силы при перемещении точки по

кривой от точки до точки . .

а) - эллипс, заданный пераметрически от точки до точки

. Найдем значение , соответствующее точке ;

Найдем значение , соответствующее точке

на : ,

(по 2.3.1)

1. Пусть плотность массы ;

;

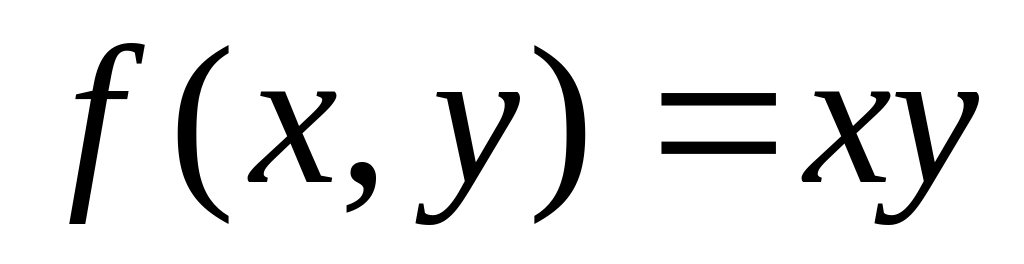Подставим вместо и их выражения через и

Для вычисления этого определенного интеграла вспомним формулы:

, ,

Тогда

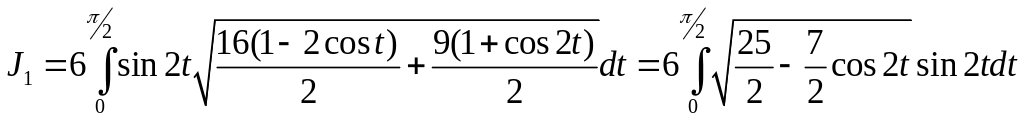
Сделаем замену переменной . Тогда ,т.е

при ; при ;

Получим

Сделаем замену переменной . Тогда т.е ;

При , при ;

Получаем

. Ответ ;

2. Найти работу силы

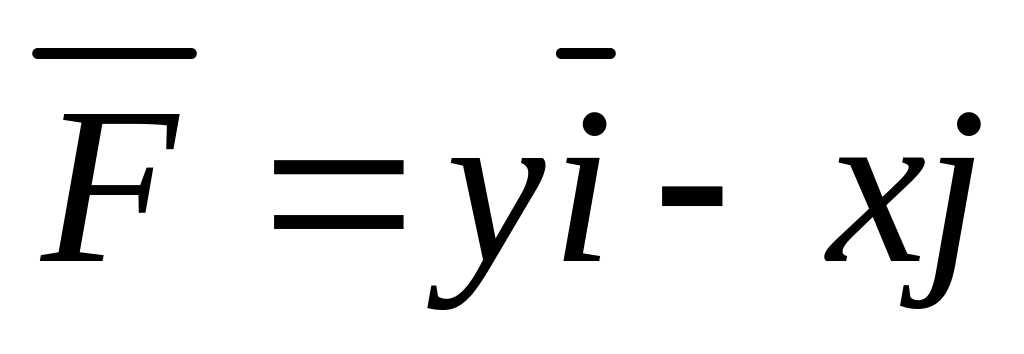
Подставим вместо , их выражения через и

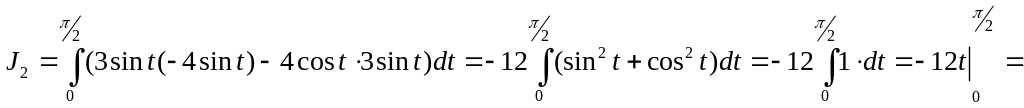
(Использовали формулу: )

Пример 3. Вычислить заряд с плотностью , распределенный по

поверхности , отсекаемой координатами плоскостями.

Решение. Заряд

Представим уравнение поверхности в виде . Тогда частные производные

и .

Подставим вместо его выражение из уравнения поверхности .

- проекция поверхности на плоскость - это треугольник .

Уравнение линии : , т.е. .

Координаты точки : ; ;

=

=

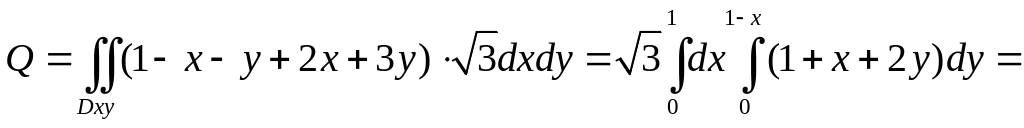
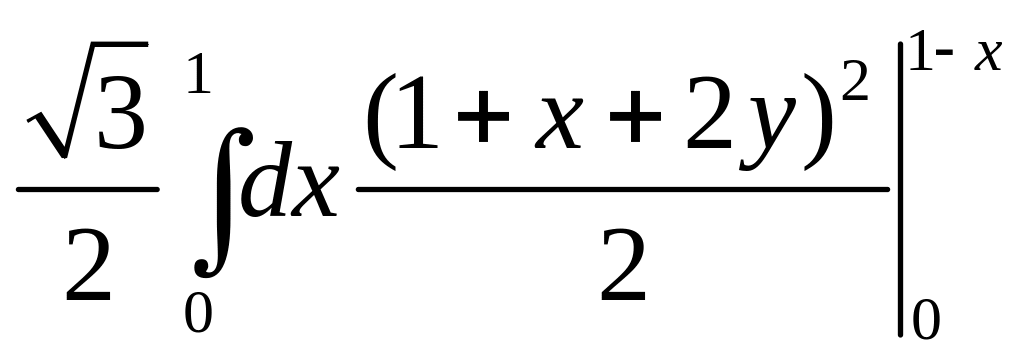Ответ: суммарный заряд .

Пример 4 : Даны векторное поле и плоскость (р), которая совместно с координатными плоскостями образует пирамиду . Пусть – основание пирамиды, принадлежащее плоскости (р), – контур, ограничивающий , – нормаль к , направленная вне пирамиды .

а

1

1

1

С

z

) вычислить поток векторного поля через поверхность (т.е. АВС) в направлении нормали .

;

По формуле 3.1.1 поток векторного поля

В

А

у

0

х

. Знаки здесь определяются наглядно. Существует формула для единичного нормального вектора к поверхности . .

D

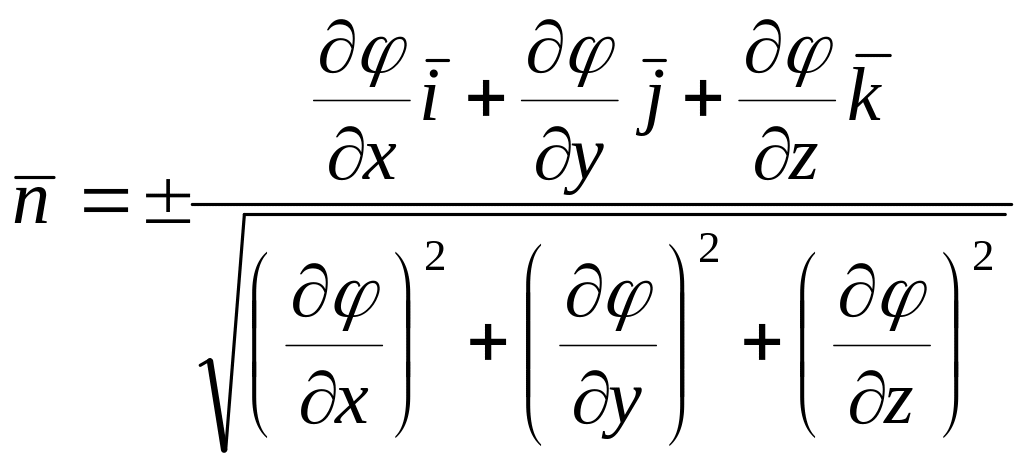В данном случае ; по условию задачи – внешняя, следовательно и в формуле, определяющей надо взять знак «+». Тогда . . – элемент поверхности АВС. Перейдем в правой части равенства от поверхностного интеграла к двойному: . Заменив z из уравнения поверхности АВС: , получим .

б) Вычислить циркуляцию по замкнутому контуру (формулы 4.2 и 2.3.2). Контур составлен из отрезков АВ, ВС и СА, направление обхода указано стрелками. .

АВ: .

Выразим , .

ВС: .

Выразим , .

СА: .

Выразим , .

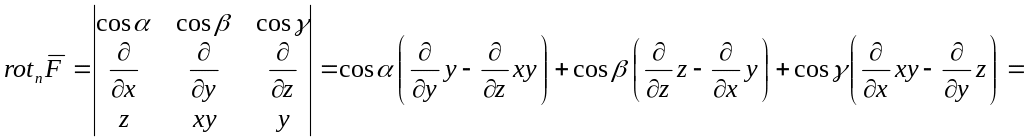
Вычислим циркуляцию по формуле Стокса ; S – поверхность АВС: . Находим (мы нашли раньше, что ).

. Перейдем в правой части к двойному интегралу по . ; .

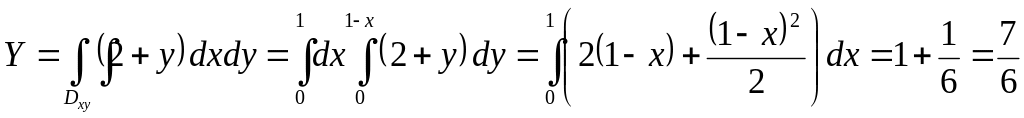Итак, циркуляция вектора по замкнутому контуру , найденная двумя способами, равна .

в) Определить поток векторного поля через полную поверхность пирамиды в направлении внешней нормали к её поверхности непосредственно и применив теорему Остроградского. Сделать чертёж.

Решение: Используем формулы 4.1.1), 4.1.2), 4.3.1).

1

z

0

D_xz

D_yz

n₂

n₃

1

1

()

) Найдем поток ∏ вектора как сумму потоков через грани . Направление внешних нормалей к граням указано стрелками на чертеже. .

y

D_xy

A

n₁

1

т.к. направлена в сторону . .

x

;

т.к. направлена в сторону , то

;

(т.к. направлена в сторону ),

; ;

Поток через поверхность АСВ был найден в задаче 3а) .

Поток через полную поверхность пирамиды .

Найдем поток П по теореме Остроградского , где – внешняя нормаль к поверхности. Находим . По формуле 4.3.2) получаем, имея .

Вывод: Поток вектора через полную поверхность , полученный двумя способами, равен .

Пример 5: Дано поле . Является ли оно соленоидальным или потенциальным?

а) , следовательно поле не является соленоидальным.

б)

.

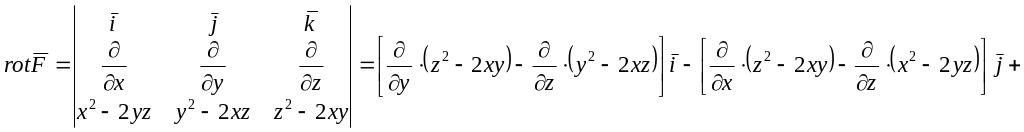
Следовательно, поле потенциальное. Потенциал поля находим по формуле (5.3)