Контрольная работа № 8 для зрф
Тема: «Дифференциальные уравнения»
Краткая теория и методические указания для решения:
Дифференциальные уравнения I порядка:
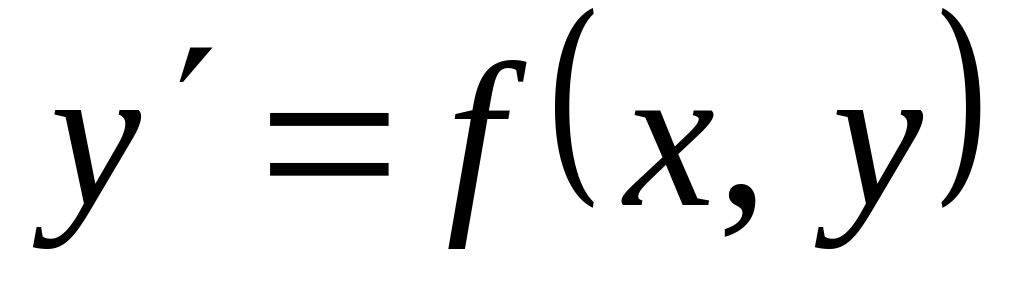или
или
.
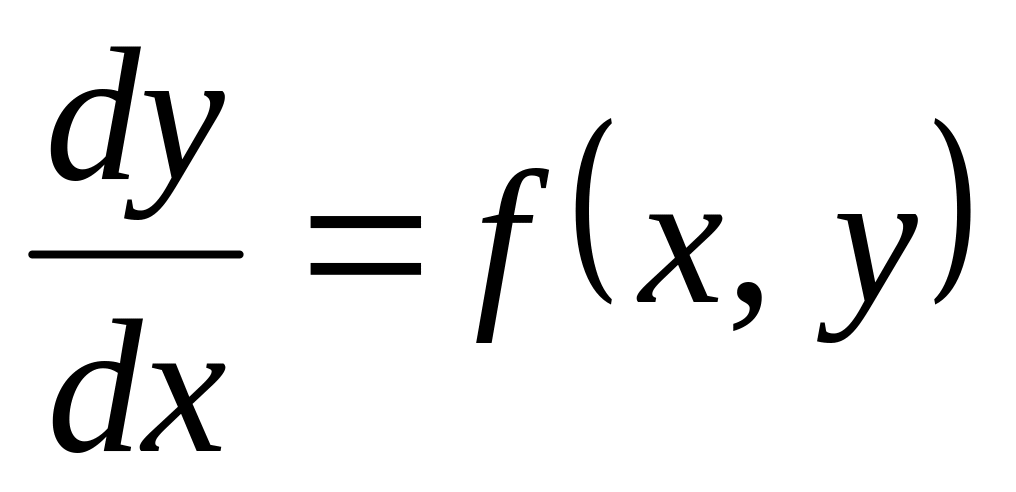Общее решение – это совокупность
решений
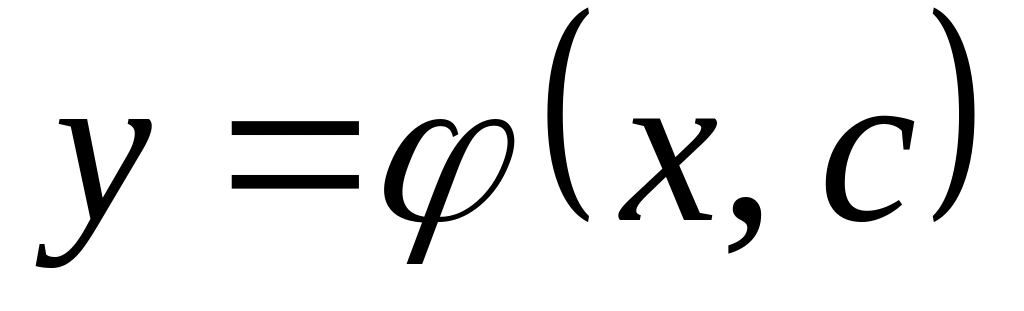или
,
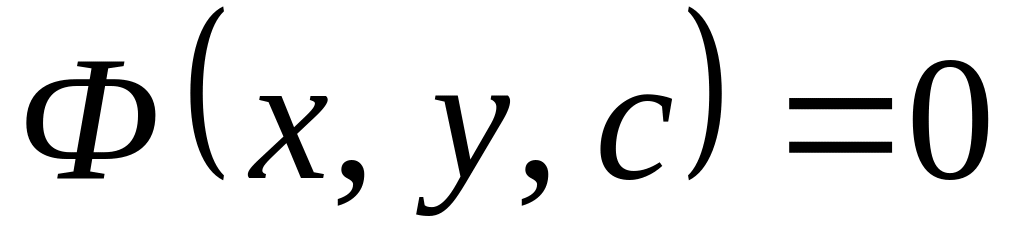зависящих от произвольной постоянной
С.
Виды и методы решения некоторых дифференциальных уравнений I порядка:
Уравнения с разделяющимися переменными
Алгоритм решения:
а)
;
Умножим на
обе части уравнения. Получим б)
;
в) Разделим переменные, чтобы слева были
функции, зависящие от у, а справа –
от х. Для этого разделим обе части
уравнения на
.
Получим
;
г) Произведя интегрирование (слева по , справа по ) получим решение
.
Однородные дифференциальные уравнения I порядка
,
где
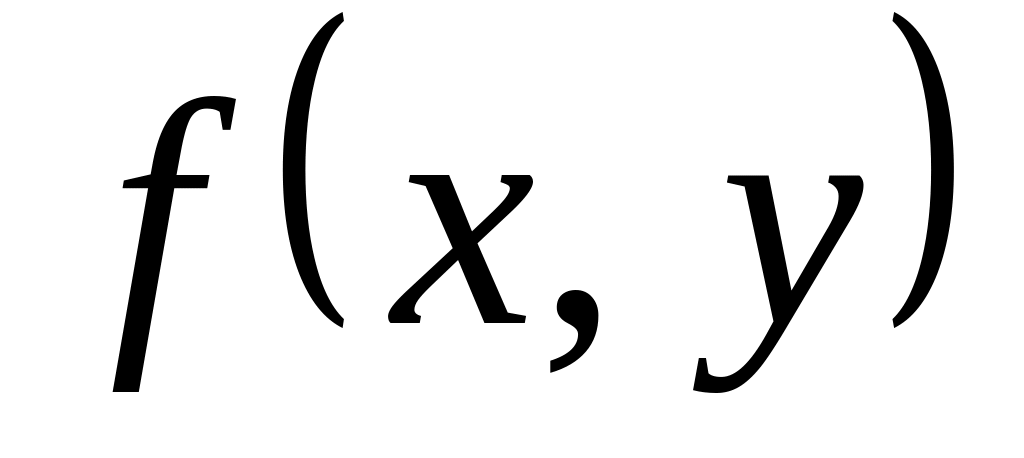имеет вид или может быть приведена в
виду
,
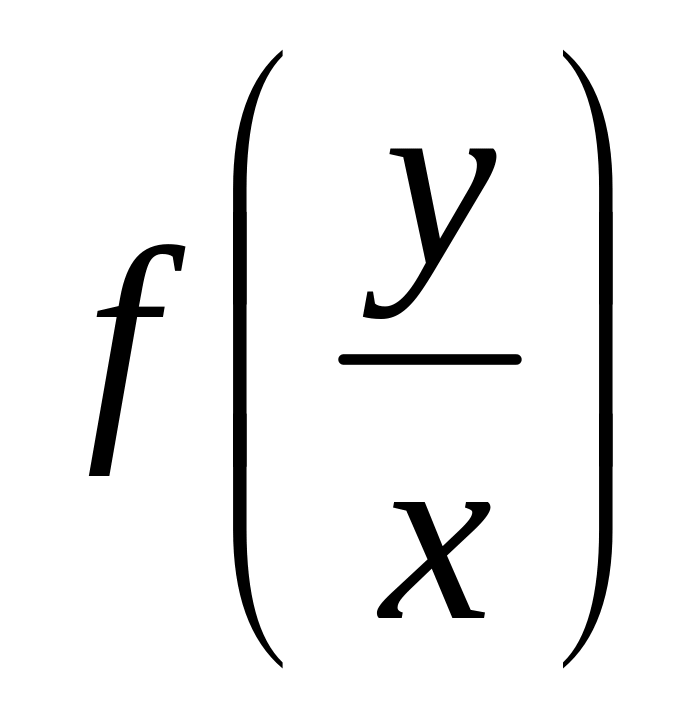тогда уравнение
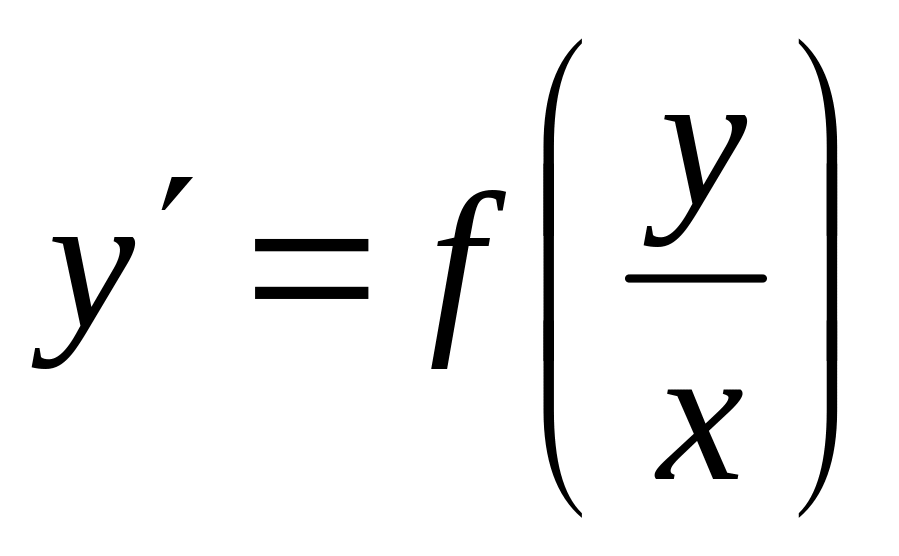заменой
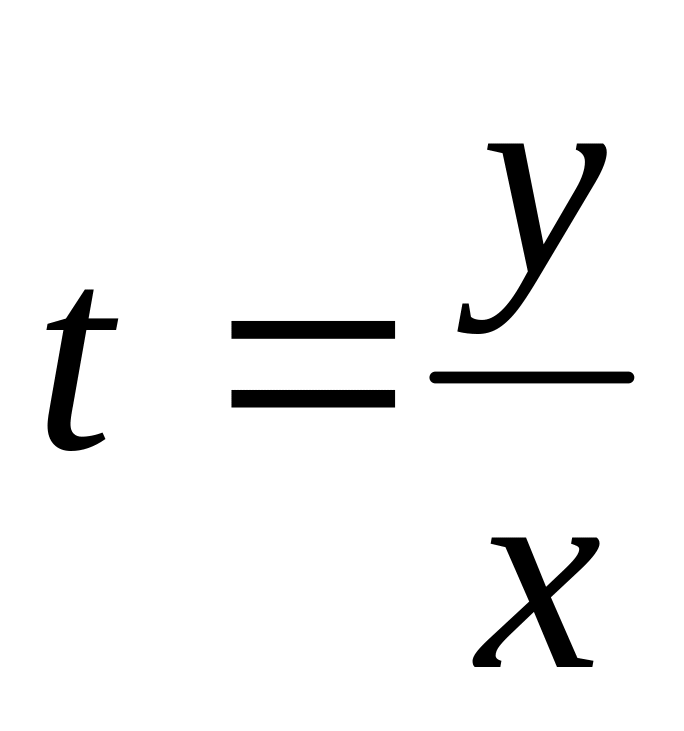приводится к уравнению с разделяющимися
переменными. Получаем
и уравнение принимает вид
,
т.е.
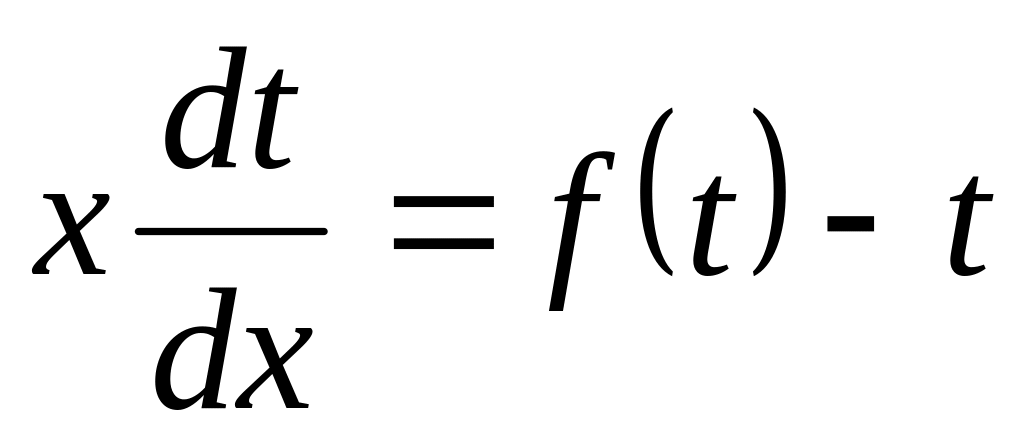и
.
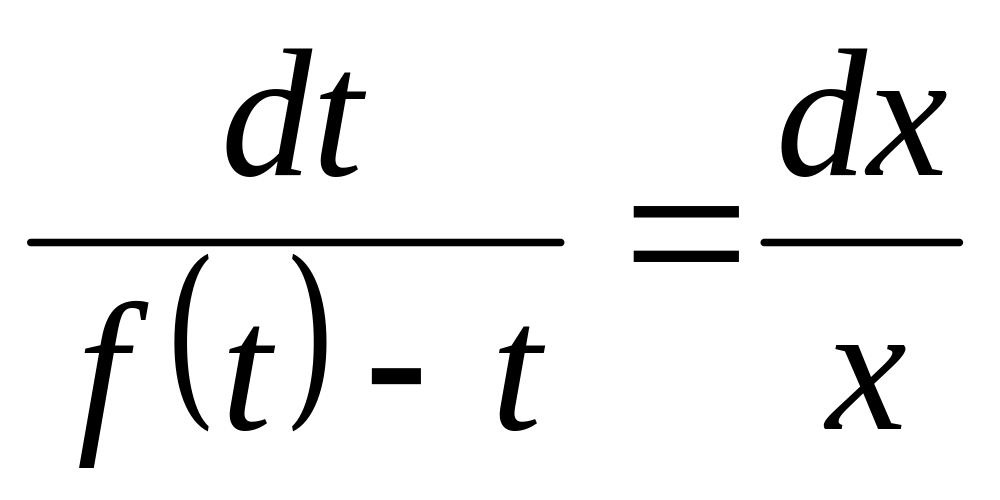
Решив это уравнение, получим t
как функцию от х. Подставив
,
получим решение уравнения в неявном
виде.
Примечание. Дроби
и
приводятся к виду
делением числителя и знаменателя на
одно и то же выражение:
на
,
на
.
Линейные дифференциальные уравнения I порядка
(
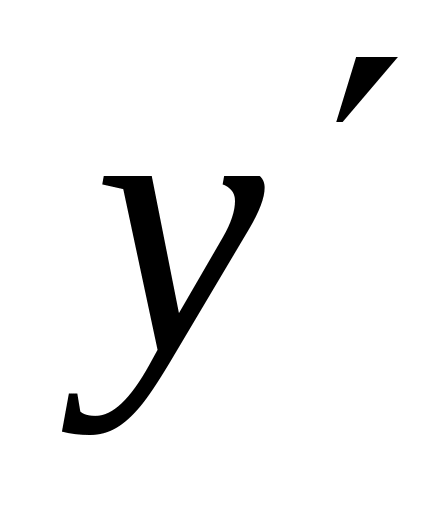и у входят в первой степени). Методом
Бернулли заменой
приводим к последовательному решению
двух уравнений с разделяющимися
переменными относительно
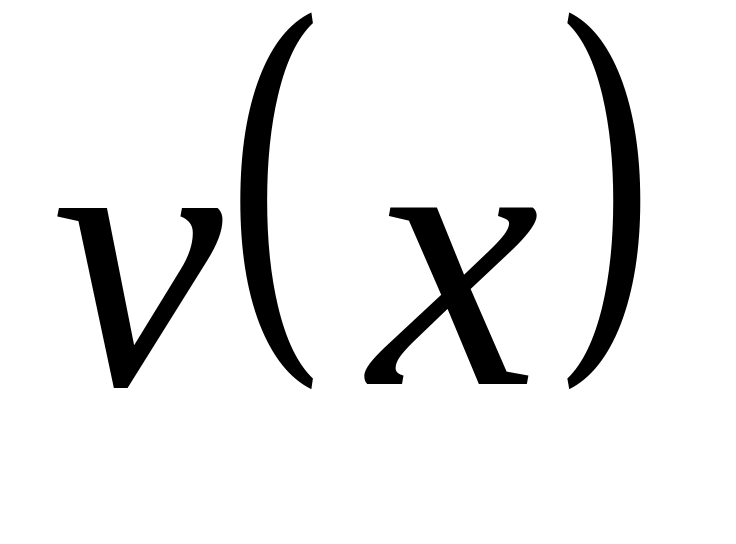и затем
.
.
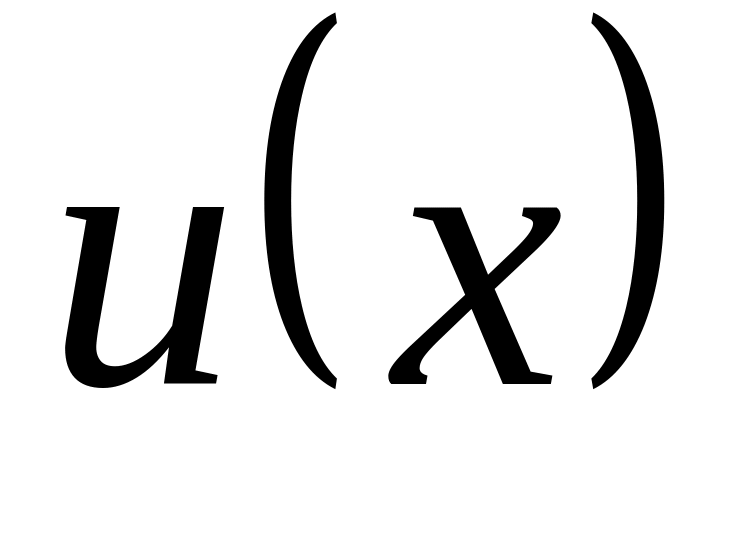Подставим в уравнение:
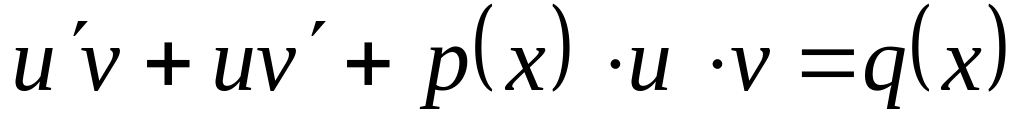или
(1.2.1) . Определим
таким образом:
.
Решив это уравнение, одно частное
решение
подставим в (1.2.1) . Получим уравнение
относительно
:
.
Определим общее решение
.
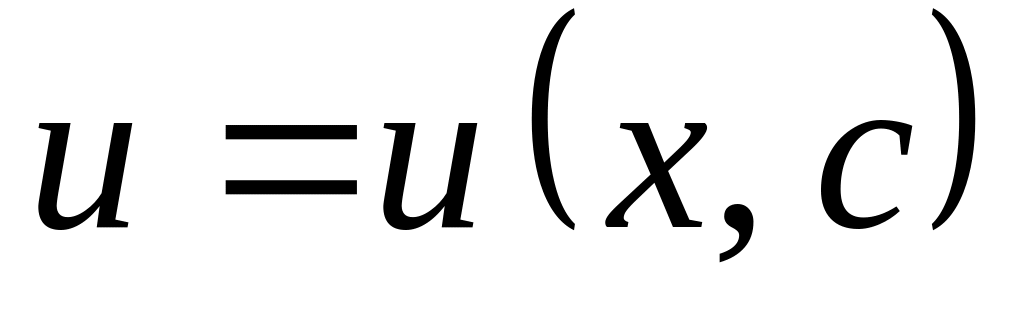Общее решение уравнения 1.2 есть
.
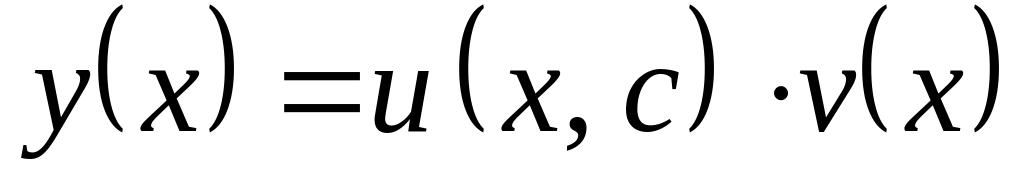1.4 Уравнения в полных дифференциалах.
Уравнение
может быть записано в дифференциальной
форме:
1.4.1
Это уравнение называется уравнением в полных дифференциалах, если
,
т.е. является полным дифференциалом
функ-
ции
.
При этом
,
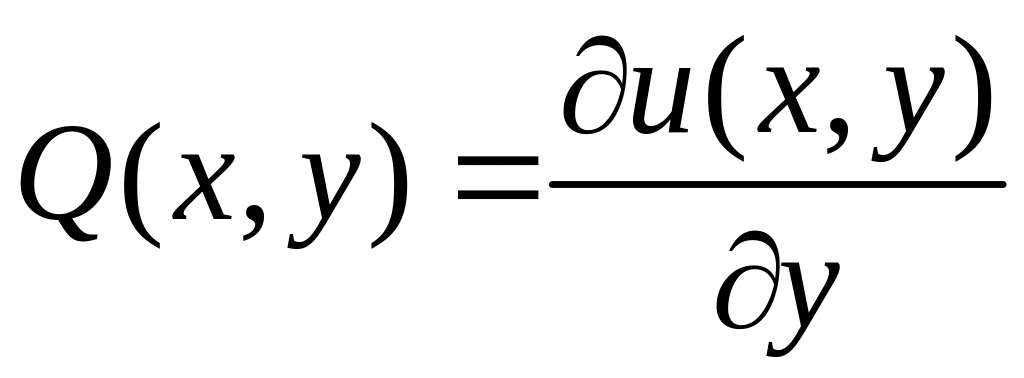1.4.2
Для того, чтобы выражение
,
необходимо и доста-
точно, чтобы выполнялось условие
1.4.3
.
Тогда уравнение 1.4.1 имеет вид
.
1.4.4 Общее решение этого уравнения
(
-
произвольная постоянная).
1.4.5 Метод нахождения функции .
Интегрируем равенство (1.4.2)
по
при фиксированном
(при этом произвольная постоянная может зависеть от ). Получим
1.4.6
.
По равенству 1.4.2
,
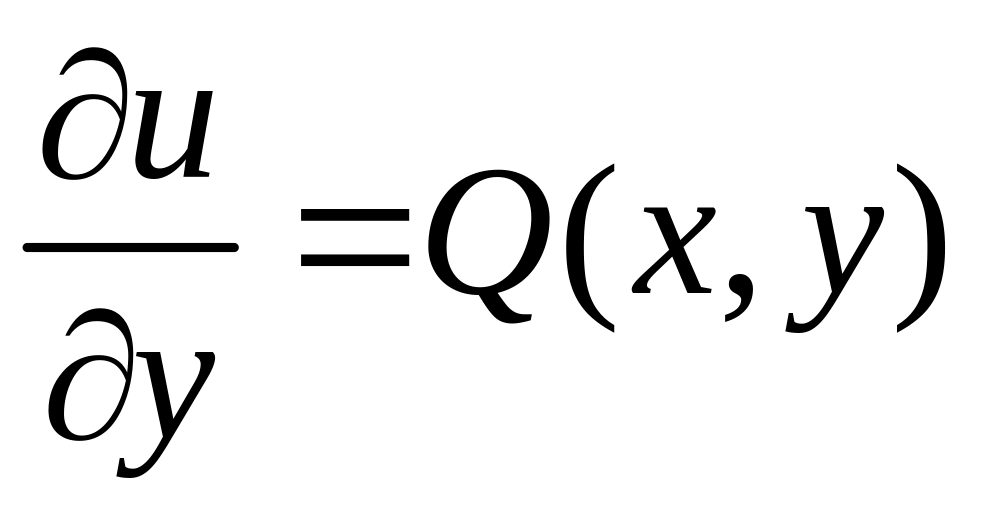тогда
,
откуда
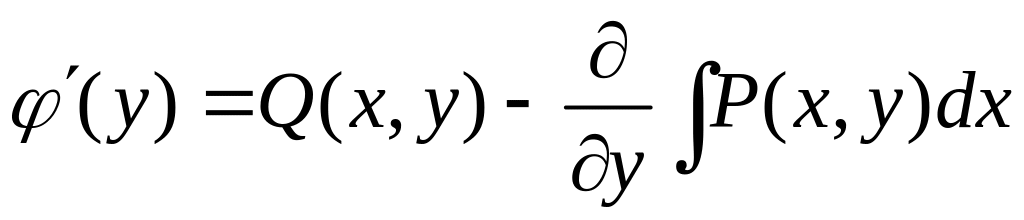
Благодаря условию 1.4.3 в правой части этого уравнения будет только функция
от .
Находим
интегрированием
по
,
подставляем в 1.4.6 и в 1.4.4.
2. Дифференциальные уравнения II
порядка.
.
Общее решение – это совокупность решений
вида
,
где
и
– произвольные постоянные.
2.1 Дифференциальные линейные уравнения
II порядка с постоянными
коэффициентами.
,
и
– постоянные числа. Если
,
то уравнение называется однородным,
если
,
то неоднородным.
Общее решение неоднородного уравнения
,
где
– общее решение однородного уравнения,
– какое-нибудь частное решение
неоднородного уравнения.
2.1.1. Решение однородного линейного уравнения II порядка
Составим и решим характеристическое
уравнение
.
Дискриминант
.
Могут быть 3 случая:
а)
,
два разных действительных корня
и
,
;
б)
,
два равных действительных корня:
=
,
;
в)
,
два комплексных корня:
и
,
– мнимая единица,
,
– действительная,
–
мнимая часть комплексного числа;
.
Если
,
.
2.1.2. Нахождение частного решения
неоднородного уравнения
методом неопределённых коэффициентов
в зависимости от вида правой части
уравнения
.
и – корни характеристического уравнения.
2.1.2.1.
(а и
– данные числа)
а)
,
,
;
б)
,
или
.
2.1.2.2.
а)
,
,
;
б)
,
или
.
в)
.
2.1.2.3.
(а,
,
– данные числа, а или
может быть равно 0).
а)
,
,
;
б)
или
.
Коэффициенты M и N
находят методом неопределённых
коэффициентов. Подставим
,
,
в уравнение 2.1. получим
.
Приравняем коэффициенты в левой и правой
части при одинаковых степенях х,
или при
,
или при
,
или при
,
или при
,
или при
,
или при
и
при
.
2.1.3. Частное решение дифференциального
уравнения при заданных начальных
условиях
.
Выпишем общее решение неоднородного
уравнения:
,
найдем
.
Подставим начальные условия в выражение
для
и
,
получим систему двух уравнений
относительно
и
.
Найдя
и
,
подставим их значения в решение у.