Раздел I. Теория пределов Лекция 1. Функция действительной переменной

Ц

6

ель лекции: рассмотреть понятие функции на множестве действительных чисел; научиться классифицировать функции, находить обратные функции.

План лекции

1. Множество действительных чисел и его свойства

2. Понятие функции действительной переменной,способы задания и простейшие классы функций

3. Суперпозиция функций, обратная, неявная и параметрическая функции

4. Классификация элементарных функций

Введение

Этой лекцией начинается одна из важных тем «Математический анализ», посвященных в основном исследованию функций.

В предыдущем семестре в теме «Теория множеств» было изучено понятие функции на множестве. Очередные несколько лекций будут посвящены этим функциям, но только для действительных множеств. Напомним, что функцией называется любое бинарное отношение, которое не содержит двух пар с одинаковыми первыми элементами и разными вторыми, или другими словами, единственному элементу одного множества некоторым образом соответствует единственный элемент другого множества.

При изучении лекции следует обратить внимание и сравнить уже известные понятия «суперпозиция» и «обратная функция» из теории множеств (см. л. 1 – 4, ч. 1) с аналитическим способом задания функции в данной лекции.

Рассмотрим множество действительных чисел R, на котором будут задаваться функции, а также его свойства.

1. Множество действительных чисел и его свойства

И так, предметом математического анализа является функция и ее свойства. Основной метод математического анализа – предельный переход.

Определение 1.

Дельта-окрестностью точки называется множество точек, таких, что расстояние от любой точки x этого множества до точки меньше дельта, или .

Возьмем некоторое множество R, тогда графически дельта-окрестность может быть представлена на рис. 1.

1

7

.1. Свойства R

1. Упорядоченность.

и справедливо только одно из унарных отношений: , , .

2. Плотность.

, при .

3. Непрерывность.

и : .

2. Понятие функции действительной переменной,

способы задания и простейшие классы функций

2.1. Понятие функции действительной переменной

Зададим два множества и , обозначив их элементы и соответственно. Определение 2.

Отображение D из множества R на E из множества R, которое ставит в соответствие элементу множества D единственный элемент множества E, называется функцией. Обозначается или , или . При этом x – независимый аргумент, y – зависимая переменная (функция). D – область определения функции, E – множество ее значений.

2.2. Способы задания функции

1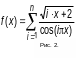 . Аналитический способ.

В виде аналитического выражения (рис. 2) зависимой переменной y от независимого аргумента x. Преимущества такого способа – компактность записи, возможность найти значение функции для любого аргумента и точность. Недостатками являются отсутствие наглядности, громоздкость вычислений.

2. Графический способ.

В виде графической зависимости (рис. 3) переменной y от независимого аргумента x. Преимущества такого способа – наглядность, возможность найти значение функции для любого аргумента. Недостатком – низкая точность, невозможность анализа функции.

3. Табличный способ.

В

8

виде табличной (известной еще со школьного курса) зависимости переменной y от независимого аргумента x (рис.4). Преимущество такого способа – быстрота определения значений функции в зависимости от аргумента. Недостатками являются низкая точность, невозможность анализа функции, ненаглядность, невозможность определения значения функции для любого значения аргумента.